2010年海南省高考文科数学试题及答案.doc

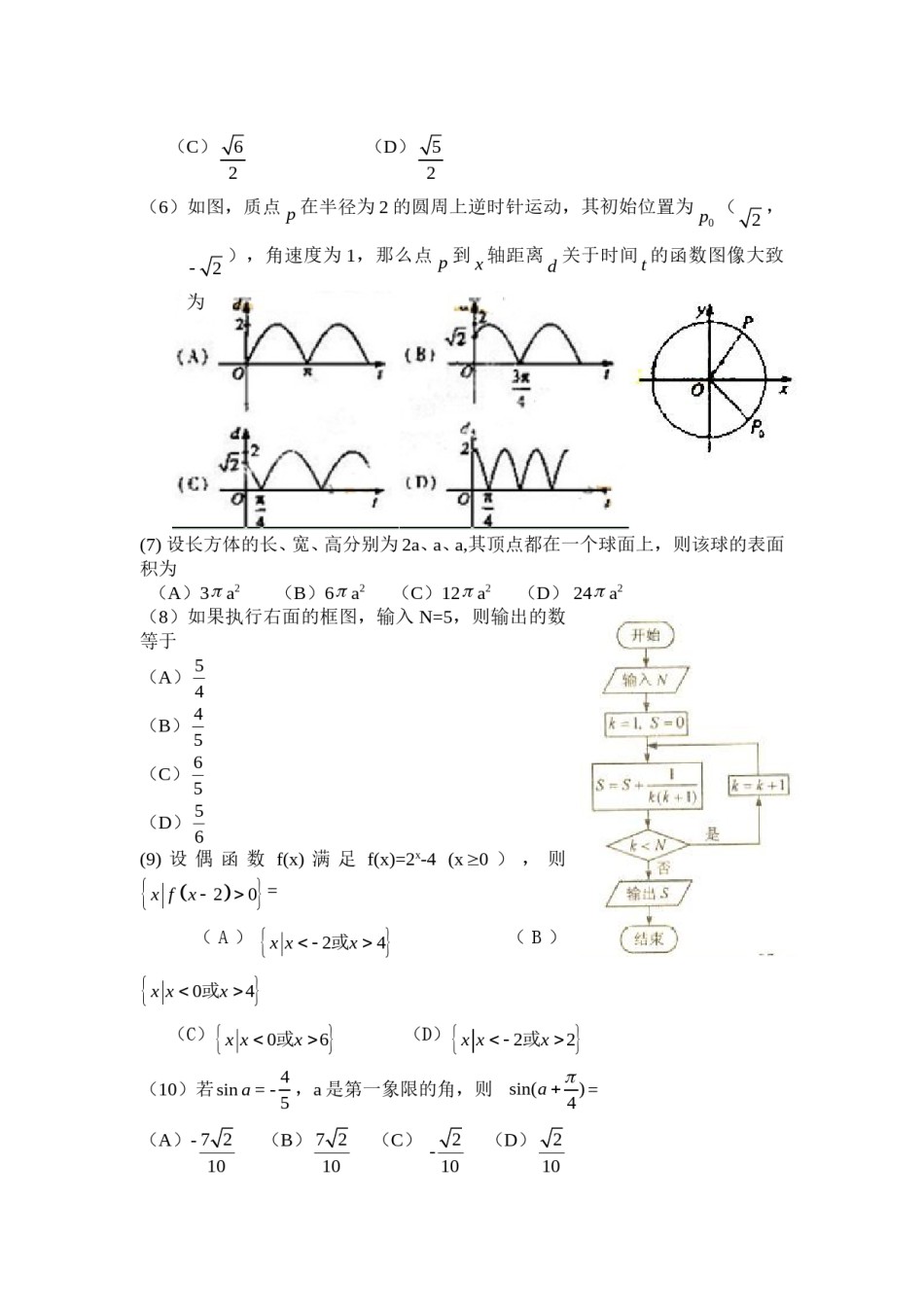
2010年普通高等学校招生全国统一考试（海南卷）文科数学参考公式：锥体体积公式样本数据x1,x2xn的标准差s1(x1x)2(x2x)2(xnx)2V1shn3其中x为样本平均数其中S为底面面积，h为高柱体体积公式球的表面积，体积公式VShS4R2,V4R3其中S为底面面积，h为高3其中R为球的半径第Ⅰ卷一、选择题：本大题共12小题，每小题5分，在每小题给出的四个选项中，只有一项是符合题目要求的。（1）已知集合Axx2,xR,Bxx4,xZ，则AB（A）（0，2）（B）[0，2]（C）0，2（D）0，1，2（2）a，b为平面向量，已知a=（4，3），2a+b=（3，18），则a，b夹角的余弦值等于（A）685（B）685（C）1665（D）1665（3）已知复数z3i，则︱z︱=(13i)2(A)14（B）12（C）1（D）2（4）曲线yx22x1在点（1,0）处的切线方程为（A）yx1（B）yx1（C）y2x2（D）y2x2（5）中心在原点，焦点在x轴上的双曲线的一条渐近线经过点（4,-2），则它的离心率为（A）6（B）5（C）6（D）522（6）如图，质点p在半径为2的圆周上逆时针运动，其初始位置为p0（2，2），角速度为1，那么点p到x轴距离d关于时间t的函数图像大致为(7)设长方体的长、宽、高分别为2a、a、a,其顶点都在一个球面上，则该球的表面积为（B）6a2（C）12a2（D）24a2（A）3a2（8）如果执行右面的框图，输入N=5，则输出的数等于f(x)满足f(x)=2x-4(x0），则（A）54（B）54（C）65（D）56(9)设偶函数xfx20=（A）xx2或x4（B）xx0或x4（C）xx0或x6（D）xx2或x2（10）若sina=-54，a是第一象限的角，则sin(a4)=（A）-72（B）72（C）-2（D）210101010（11）已知ABCD的三个顶点为A（-1，2），B（3，4），C（4，-2），点（x，y）在ABCD的内部，则z=2x-5y的取值范围是（A）（-14，16）（B）（-14，20）（C）（-12，18）（D）（-12，20）（12）已知函数f(x)=lgx1,0x10若a，b，c互不相等，且f(a)=f(b)=12x6,x0f(c)，则abc的取值范围是（A）（1，10）（B）(5，6)（C）(10，12)（D）(20，24)第Ⅱ卷本卷包括必考题和选考题两部分。第（13）题～第（21）题为必考题，每个试题考生都必须做答。第（22）题～第（24）题为选考题，考生根据要求做答。二、填空题：本大题共4小题，每小题5分。（13）圆心在原点上与直线xy20相切的圆的方程为。（14）设函数yf(x)为区间0,1上的图像是连续不断的一条曲线，且恒有0fx1，可以用随机模拟方法近似计算由曲线yf(x)及直线x0，x1，y0所围成部分的面积S，先产生两组（每组N个）区间0,1上的均匀随机数x1,x2.....xn和y1,y2.....yn，由此得到N个点（xi，yi）（i=1，2，…，N）.再数出其中满足yy1i≤ff((xx)i(i1,2.....N)的点数N1，那么由随机模拟方法可得S的近似值为___________(15)一个几何体的正视图为一个三角形，则这个几何体可能是下列几何体中的_______(填入所有可能的几何体前的编号)①三棱锥②四棱锥③三棱柱④四棱柱⑤圆锥⑥圆柱(16)在△ABC中，D为BC边上一点，BC3BD,AD2,ADB135.若AC2AB，则BD=________.三、解答题：解答应写出文字说明，证明过程或演算步骤。（17）（本小题满分12分）设等差数列an满足a35，a109。（Ⅰ）求an的通项公式；（Ⅱ）求an的前n项和Sn及使得Sn最大的序号n的值。（18）（本小题满分12分）如图，已知四棱锥PABCD的底面为等腰梯形，AB∥CD,ACBD,垂足为H，PH是四棱锥的高。（Ⅰ）证明：平面PAC平面PBD；（Ⅱ）若AB6,APBADB60°,求四棱锥PABCD的体积。请考生在第（22）、（23）、（24）三题中任选一题作答，如果多做，则按所做的第一题计分。作答时用2B铅笔在答题卡上把所选题目的题号涂黑。（19）（本小题满分12分）为调查某地区老年人是否需要志愿者提供帮助，用简单随机抽样方法从该地区调查了500位老人，结果如下：（Ⅰ）估计该地区老年人中，需要志愿者提供帮助的老年人的比例；（Ⅱ）能否有99％的把握认为该地区的老年人是否需要志愿者提供帮助与性别有关？（...