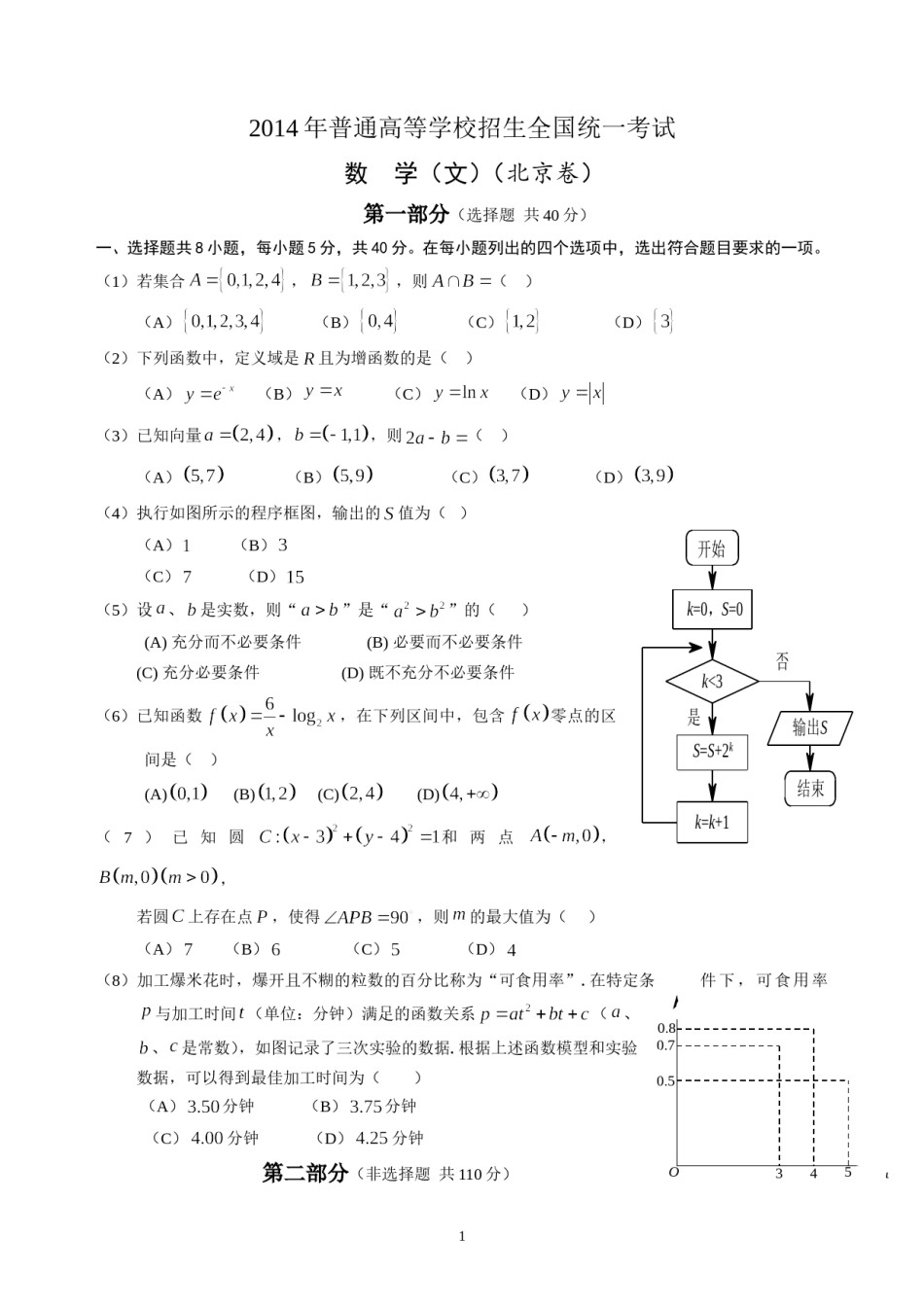
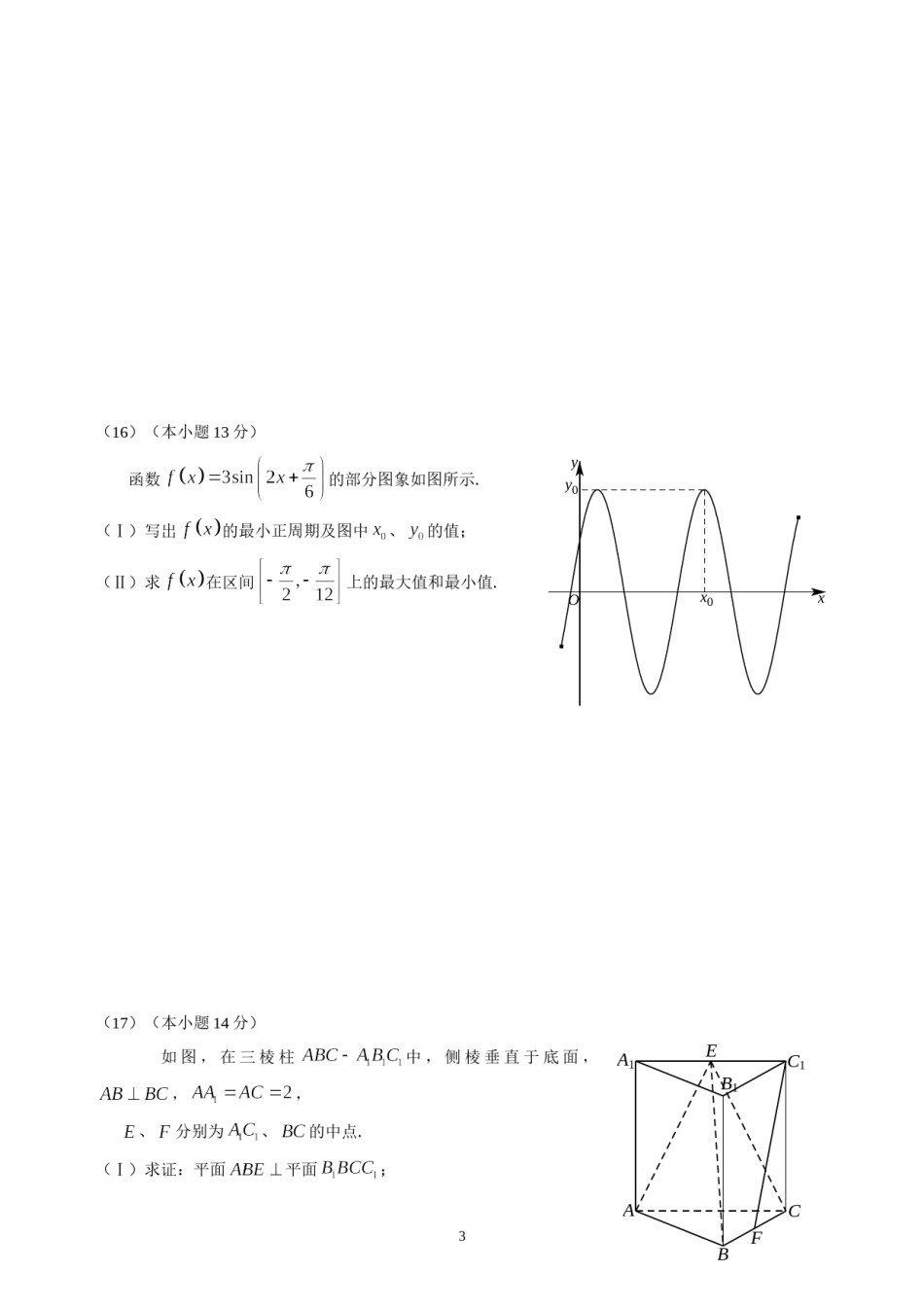
2014年普通高等学校招生全国统一考试数学(文)(北京卷)第一部分(选择题共40分)一、选择题共8小题,每小题5分,共40分。在每小题列出的四个选项中,选出符合题目要求的一项。(1)若集合,,则()(A)(B)(C)(D)(2)下列函数中,定义域是且为增函数的是()(A)(B)(C)(D)(3)已知向量,,则()(A)(B)(C)(D)(4)执行如图所示的程序框图,输出的值为()(A)(B)开始(C)(D)(5)设、是实数,则“”是“”的()k=0,S=0(A)充分而不必要条件(C)充分必要条件(B)必要而不必要条件k<3否是输出S(D)既不充分不必要条件S=S+2k结束(6)已知函数,在下列区间中,包含零点的区k=k+1间是()(A)(B)(C)(D)(7)已知圆和两点,,若圆上存在点,使得,则的最大值为()(A)(B)(C)(D)(8)加工爆米花时,爆开且不糊的粒数的百分比称为“可食用率”.在特定条件下,可食用率p与加工时间(单位:分钟)满足的函数关系(、0.8、是常数),如图记录了三次实验的数据.根据上述函数模型和实验0.7数据,可以得到最佳加工时间为()0.5(A)分钟(B)分钟(C)分钟(D)分钟第二部分(非选择题共110分)O345t1二、填空题共6小题,每小题5分,共30分。(9)若,则.(10)设双曲线的两个焦点为,,一个顶点式,则的方程为.(11)某三棱锥的三视图如图所示,则该三棱锥的最长棱的棱长为.(12)在中,,,,则;.(13)若、满足,则的最小值为.2(14)顾客请一位工艺师把、两件玉石原料各制成一件工艺品,工艺师带一位徒弟完成这项任务,每件颜料先由徒弟完成粗加工,21正(主)视图侧(左)视图再由工艺师进行精加工完成制作,两件工艺品都完成后交付顾客,11两件原料每道工序所需时间(单位:工作日)如下:工序时间粗加工俯视图原料精加工原料原料则最短交货期为工作日.三、解答题共6小题,共80分。解答应写出必要的文字说明,演算步骤。(15)(本小题13分)已知是等差数列,满足,,数列满足,,且为等比数列.(Ⅰ)求数列和的通项公式;(Ⅱ)求数列的前项和.2(16)(本小题13分)函数的部分图象如图所示.yy0(Ⅰ)写出的最小正周期及图中、的值;(Ⅱ)求在区间上的最大值和最小值.x0xO(17)(本小题14分)如图,在三棱柱中,侧棱垂直于底面,A1EC1,,B1、分别为、的中点.(Ⅰ)求证:平面平面;ACBF3(Ⅱ)求证:平面;(Ⅲ)求三棱锥的体积.组号分组频数(18)(本小题14分)16频数28317从某校随机抽取100名学生,获得了他们一周课外阅读时间422组距525612(单位:小时)的b数据,整理得到数据分组及频数分布表和频率分76布直方图:8292a合计1004O24681012141618阅读时间(Ⅰ)从该校随机选取一名学生,试估计这名学生该周课外阅读时间少于12小时的概率;(Ⅱ)求频率分布直方图中的a,b的值;(Ⅲ)假设同一组中的每个数据可用该组区间的中点值代替,试估计样本中的100名学生该周课外阅读时间的平均数在第几组(只需写出结论)(19)(本小题14分)已知椭圆C:.(Ⅰ)求椭圆C的离心率;(Ⅱ)设O为原点,若点A在直线,点B在椭圆C上,且,求线段AB长度的最小值.5(20)(本小题13分)已知函数.(Ⅰ)求在区间上的最大值;(Ⅱ)若过点存在3条直线与曲线相切,求t的取值范围;(Ⅲ)问过点分别存在几条直线与曲线相切?(只需写出结论)62014年普通高等学校招生全国统一考试数学(文)(北京卷)答案及解析第一部分(选择题共40分)一、选择题共8小题,每小题5分,共40分。在每小题列出的四个选项中,选出符合题目要求的一项。(1)若集合,,则()(A)(B)(C)(D)【答案】C,所以选C.【解析】因为7【考点】本小题主要考查集合的基本运算,属容易题,熟练集合的基础知识是解答集合题目的关键.(2)下列函数中,定义域是且为增函数的是()(A)(B)(C)(D)【答案】B;选项D,在上是减函数,【解析】对于选项A,在R上是减函数;选项C的定义域为故选B.【考点】本小题主要考查函数的单调性,属基础题,难度不大.(3)已知向量,,则()(A)(B)(C)(D)【答案】A【解析】因为,所以,故选A.【考点】本小题主要考查平面向量的基本运算,属容易...