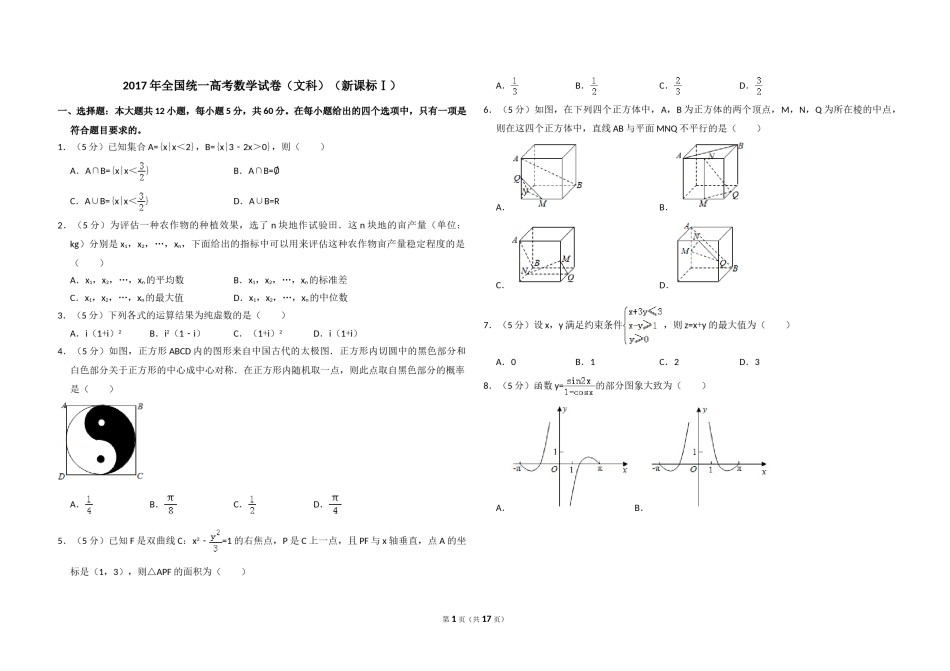
2017年全国统一高考数学试卷(文科)(新课标Ⅰ)A.B.C.D.一、选择题:本大题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是6.(5分)如图,在下列四个正方体中,A,B为正方体的两个顶点,M,N,Q为所在棱的中点,符合题目要求的。则在这四个正方体中,直线AB与平面MNQ不平行的是()1.(5分)已知集合A={xx<2},B={x3﹣2x>0},则()A.A∩B={xx<}B.A∩B=∅C.A∪B={xx<}D.A∪B=RA.B.2.(5分)为评估一种农作物的种植效果,选了n块地作试验田.这n块地的亩产量(单位:kg)分别是x1,x2,…,xn,下面给出的指标中可以用来评估这种农作物亩产量稳定程度的是()B.x1,x2,…,xn的标准差C.D.A.x1,x2,…,xn的平均数C.x1,x2,…,xn的最大值D.x1,x2,…,xn的中位数3.(5分)下列各式的运算结果为纯虚数的是()7.(5分)设x,y满足约束条件,则z=x+y的最大值为()A.i(1+i)2B.i2(1﹣i)C.(1+i)2D.i(1+i)4.(5分)如图,正方形ABCD内的图形来自中国古代的太极图.正方形内切圆中的黑色部分和A.0B.1C.2D.3白色部分关于正方形的中心成中心对称.在正方形内随机取一点,则此点取自黑色部分的概率是()8.(5分)函数y=的部分图象大致为()A.B.C.D.A.B.5.(5分)已知F是双曲线C:x2﹣=1的右焦点,P是C上一点,且PF与x轴垂直,点A的坐标是(1,3),则△APF的面积为()第1页(共17页)A.B.C.D.12.(5分)设A,B是椭圆C:+=1长轴的两个端点,若C上存在点M满足∠AMB=120°,则m的取值范围是()C.D.A.(0,1]∪[9,+∞)B.(0,]∪[9,+∞)C.(0,1]∪[4,+∞)9.(5分)已知函数f(x)=lnx+ln(2﹣x),则()D.(0,]∪[4,+∞)A.f(x)在(0,2)单调递增B.f(x)在(0,2)单调递减二、填空题:本题共4小题,每小题5分,共20分。C.y=f(x)的图象关于直线x=1对称13.(5分)已知向量=(﹣1,2),=(m,1),若向量+与垂直,则m=.D.y=f(x)的图象关于点(1,0)对称14.(5分)曲线y=x2+在点(1,2)处的切线方程为.10.(5分)如图程序框图是为了求出满足3n﹣2n>1000的最小偶数n,那么在15.(5分)已知α∈(0,),tanα=2,则cos(α﹣)=.和两个空白框中,可以分别填入()16.(5分)已知三棱锥S﹣ABC的所有顶点都在球O的球面上,SC是球O的直径.若平面SCA⊥平面SCB,SA=AC,SB=BC,三棱锥S﹣ABC的体积为9,则球O的表面积为.三、解答题:共70分。解答应写出文字说明、证明过程或演算过程.第17~21题为必选题,每个试题考生都必须作答。第22、23题为选考题,考生根据要求作答。(一)必考题:共60分。17.(12分)记Sn为等比数列{an}的前n项和.已知S2=2,S3=﹣6.(1)求{an}的通项公式;(2)求Sn,并判断Sn+1,Sn,Sn+2是否成等差数列.A.A>1000和n=n+1B.A>1000和n=n+2C.A≤1000和n=n+1D.A≤1000和n=n+218.(12分)如图,在四棱锥P﹣ABCD中,AB∥CD,且∠BAP=∠CDP=90°.(1)证明:平面PAB⊥平面PAD;11.(5分)△ABC的内角A,B,C的对边分别为a,b,c,已知sinB+sinA(sinC﹣cosC)=0,a=2,c=,则C=()第2页(共17页)(2)若PA=PD=AB=DC,∠APD=90°,且四棱锥P﹣ABCD的体积为,求该四棱锥的侧面积.这一天的生产过程可能出现了异常情况,需对当天的生产过程进行检查.(ⅰ)从这一天抽检的结果看,是否需对当天的生产过程进行检查?(ⅱ)在(﹣3s,+3s)之外的数据称为离群值,试剔除离群值,估计这条生产线当天生产的零件尺寸的均值与标准差.(精确到0.01)附:样本(xi,yi)(i=1,2,…,n)的相关系数r=,≈0.09.19.(12分)为了监控某种零件的一条生产线的生产过程,检验员每隔30min从该生产线上随机抽取一个零件,并测量其尺寸(单位:cm).下面是检验员在一天内依次抽取的16个零件的尺寸:抽取次序1234567820.(12分)设A,B为曲线C:y=上两点,A与B的横坐标之和为4.零件尺寸9.9510.129.969.9610.019.929.9810.04(1)求直线AB的斜率;(2)设M为曲线C上一点,C在M处的切线与直线AB平行,且AM⊥BM,求直线AB的方程.抽取次序910111213141...