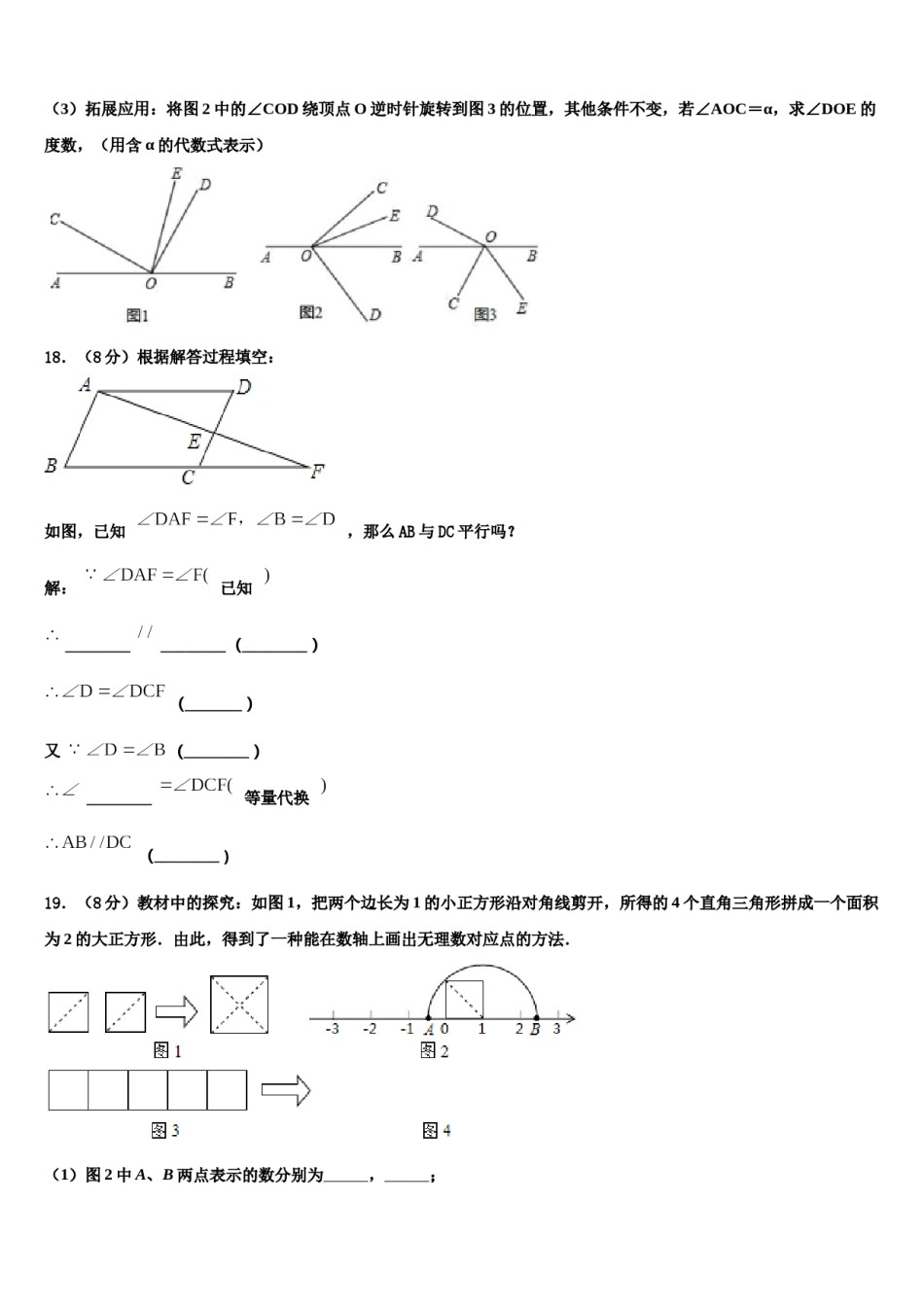
2024届绥化市重点中学数学七上期末质量检测试题注意事项铅笔作答;第二部分必须用黑1.考生要认真填写考场号和座位序号。2.试题所有答案必须填涂或书写在答题卡上,在试卷上作答无效。第一部分必须用2B色字迹的签字笔作答。3.考试结束后,考生须将试卷和答题卡放在桌面上,待监考员收回。一、选择题(每小题3分,共30分)1.如图,∠AOB的两边OA,OB均为平面反光镜,∠AOB=40°.在射线OB上有一点P,从P点射出一束光线经OA上的Q点反射后,反射光线QR恰好与OB平行,则∠QPB的度数是()A.60°B.80°C.100°D.120°2.下列图形中可以作为一个正方体的展开图的是().A.B.C.D.3.化简的结果是()A.B.C.D.04.如果以x=﹣3为方程的解构造一个一元一次方程,那么下列方程中不满足要求的是()A.x+3=0B.x﹣9=﹣12C.2x+3=﹣3D.5.2020年某市各级各类学校学生人数约为1580000人,将1580000这个数用科学记数法表示为()A.0.158×107B.15.8×105C.1.58×106D.1.58×1076.下列各数中,正确的角度互化是()A.63.5°=63°50′B.23°12′36″=23.48°C.18°18′18″=18.33°D.22.25°=22°15′7.如图,点C是线段AB的中点,点D是线段BC的中点,下列等式正确的是()A.CD=AC-DBB.CD=AB-DBC.AD=AC-DBD.AD=AB-BC8.一个家庭在今年上半年用电的度数如下:89、73、58、69、76、79,那么这个家庭平均每月用电()A.72度B.73度C.74度D.76度9.已知f(1)=2(取1×2计算结果的末位数字),f(2)=6(取2×3计算结果的末位数字),f(3)=2(取3×4计算结果的末位数字),…,则f(1)+f(2)+f(3)+…+f(2020)的值为()A.2020B.4040C.4042D.403010.已知a是两位数,b是一位数,把b接在a的后面,就成了一个三位数,这个三位数可以表示为()A.a+bB.100b+aC.100a+bD.10a+b二、填空题(本大题共有6小题,每小题3分,共18分)11.18世纪最杰出的瑞士数学家欧拉,最先把关于x的多项式用符号“f(x)”表示,如f(x)=﹣3x2+2x﹣1,把x=﹣2时多项式的值表示为f(﹣2),则f(﹣2)=_____.12.已知且则___.13.单项式的系数是___________.14.当x=时,的值为零.15.某公园的成人单价是10元,儿童单价是4元.某旅行团有a名成人和b名儿童;则旅行团的门票费用总和为_______________元.16.已知x=2是关于x的方程的解,则a的值是______.三、解下列各题(本大题共8小题,共72分)17.(8分)已知直线AB过点O,∠COD=90°,OE是∠BOC的平分线.(1)操作发现:①如图1,若∠AOC=40°,则∠DOE=②如图1,若∠AOC=α,则∠DOE=(用含α的代数式表示)(2)操作探究:将图1中的∠COD绕顶点O顺时针旋转到图2的位置,其他条件不变,②中的结论是否成立?试说明理由.(3)拓展应用:将图2中的∠COD绕顶点O逆时针旋转到图3的位置,其他条件不变,若∠AOC=α,求∠DOE的度数,(用含α的代数式表示)18.(8分)根据解答过程填空:如图,已知,那么AB与DC平行吗?解:已知________________(________)(_______)又(________)________等量代换(________)19.(8分)教材中的探究:如图1,把两个边长为1的小正方形沿对角线剪开,所得的4个直角三角形拼成一个面积为2的大正方形.由此,得到了一种能在数轴上画出无理数对应点的方法.(1)图2中A、B两点表示的数分别为,;(2)请你参照上面的方法,把长为5,宽为1的长方形进行裁剪,拼成一个正方形.①在图3中画出裁剪线,并在图4位置画出所拼正方形的示意图.②在数轴上分别标出表示数以及﹣3的点,(图中标出必要线段长)20.(8分)如图,已知直线AB以及点C、点D、点E(1)画直线CD交直线AB于点O,画射线OE(2)在(1)所画的图中,若∠AOE=40°,∠EOD∶∠AOC=3∶4,求∠AOC的度数21.(8分)先化简,再求值:(-4x2-2x+8)-(x-1),其中x=22.(10分)已知关于x的方程4x+2m=3x+1和方程3x+2m=6x+1的解相同,(1)求m的值;(2)求代数式(-2m)2020-(m)2019的值.23.(10分)计算.24.(12分)(5分)如图,点C、D在线段AB上,且AC=CD=DB,点E是线段AC的中点,若ED=12cm,求AB的长度.参考答案一...