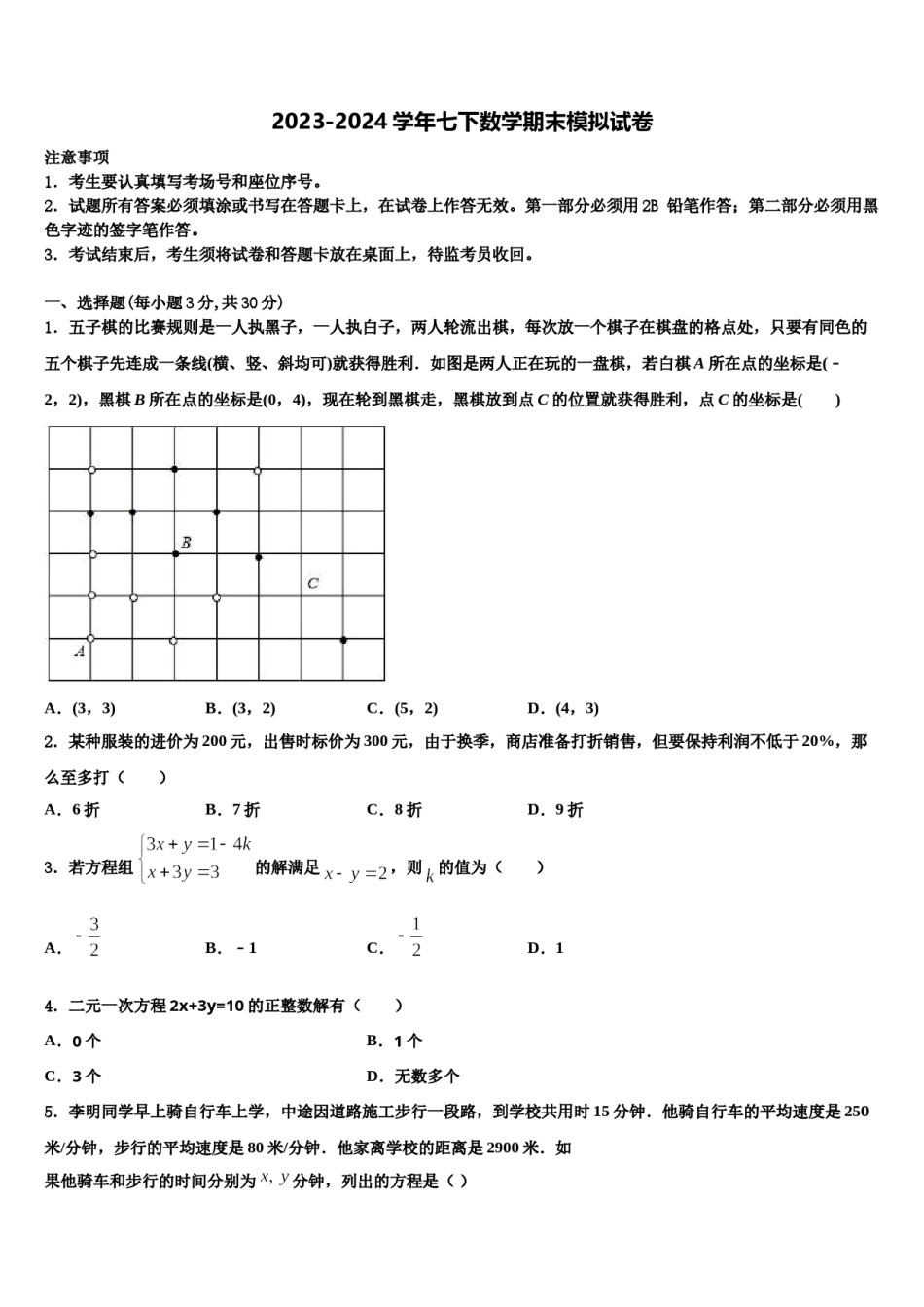
2023-2024学年七下数学期末模拟试卷注意事项铅笔作答;第二部分必须用黑1.考生要认真填写考场号和座位序号。2.试题所有答案必须填涂或书写在答题卡上,在试卷上作答无效。第一部分必须用2B色字迹的签字笔作答。3.考试结束后,考生须将试卷和答题卡放在桌面上,待监考员收回。一、选择题(每小题3分,共30分)1.五子棋的比赛规则是一人执黑子,一人执白子,两人轮流出棋,每次放一个棋子在棋盘的格点处,只要有同色的五个棋子先连成一条线(横、竖、斜均可)就获得胜利.如图是两人正在玩的一盘棋,若白棋A所在点的坐标是(﹣2,2),黑棋B所在点的坐标是(0,4),现在轮到黑棋走,黑棋放到点C的位置就获得胜利,点C的坐标是()A.(3,3)B.(3,2)C.(5,2)D.(4,3)2.某种服装的进价为200元,出售时标价为300元,由于换季,商店准备打折销售,但要保持利润不低于20%,那么至多打()B.7折C.8折D.9折A.6折3.若方程组的解满足,则的值为()A.B.﹣1C.D.14.二元一次方程2x+3y=10的正整数解有()A.0个B.1个C.3个D.无数多个5.李明同学早上骑自行车上学,中途因道路施工步行一段路,到学校共用时15分钟.他骑自行车的平均速度是250米/分钟,步行的平均速度是80米/分钟.他家离学校的距离是2900米.如果他骑车和步行的时间分别为分钟,列出的方程是()A.B.C.D.6.已知a,b,c是△ABC的三条边长,化简a+b﹣c+b﹣a﹣c的结果为()A.2a+2bB.2a+2b﹣2cC.2b﹣2cD.2a7.若面积为15的正方形的边长为x,则x的范围是()A.3<x<4B.4<x<5C.5<x<6D.6<x<78.若分式方程无解,则的值为()A.0B.6C.0或6D.0或9.某校七年级共720名学生参加数学测试,随机抽取50名学生的成绩进行统计,其中15名学生的成绩达到优秀,估计计该校七年级学生在这次数学测试中,达到优秀的学生人数约有A.140人B.144人C.210人D.216人10.观察下面图案在A、B、C、D四幅图案中,能通过图案平移得到的是()A.B.C.D.二、填空题(本大题共有6小题,每小题3分,共18分)11.把方程变形,用含x的代数式表示y,则y=______________.12.如图所示,A、B、C、D在同一直线上,AB=CD,DE∥AF,若要使△ACF≌△DBE,则还需要补充一个条件:_____.13.计算:3×9=_____.14.温度由下降后是________.15.若和都是关于x,y的方程y=kx+b的解,则k+2b的值是________.16.由,可得到用表示的式子为_______.(用含的式子表示)三、解下列各题(本大题共8小题,共72分)17.(8分)如图,四边形ABCD中,AD∥BC,∠ABC=90°.(1)直接填空:∠BAD=______°.(2)点P在CD上,连结AP,AM平分∠DAP,AN平分∠PAB,AM、AN分别与射线BP交于点M、N.设∠DAM=α°.①求∠BAN的度数(用含α的代数式表示).②若AN⊥BM,试探究∠AMB的度数是否为定值?若为定值,请求出该定值;若不为定值,请用α的代数式表示它.18.(8分)解答下列各题解方程:解方程组:19.(8分)已知点A(﹣1,0)、B(3,0)、C(3,2)(1)求证:BC⊥x轴;(2)求△ABC的面积;(3)若在y轴上有一点P,使S△ABP=2S△ABC,求点P的坐标.20.(8分)如图,在平面直角坐标系中,OA=OB=OC=6,过点A的直线AD交BC于点D,交y轴与点G,△ABD的面积为△ABC面积的.(1)求点D的坐标;(2)过点C作CE⊥AD,交AB交于F,垂足为E.①求证:OF=OG;②求点F的坐标。(3)在(2)的条件下,在第一象限内是否存在点P,使△CFP为等腰直角三角形?若存在,直接写出点P坐标;若不存在,请说明理由。21.(8分)解不等式或不等式组(1)解不等式≤,并在数轴上表示解集.(2)解不等式组22.(10分)((1)解方程组(2)解方程组;23.(10分)解不等式组,把它的解集在数轴上表示出来,并写出这个不等式组的正整数解.24.(12分)母亲节过后,某校在本校学生中做了一次抽样调查,并把调查的结果分成三种类型:A.不知道那一天是母亲节的;B.知道但没有行动的;C.知道并问候母亲的.如图是根据调查结果绘制的统计图(部分).(1)已知A类学生占被调查学生人数的,则被调查的学生共有多少人?(2)计算B类学生的人数并根据计算结果补全统计图;(3)如果该校共有学生2000人,你估计这个学...