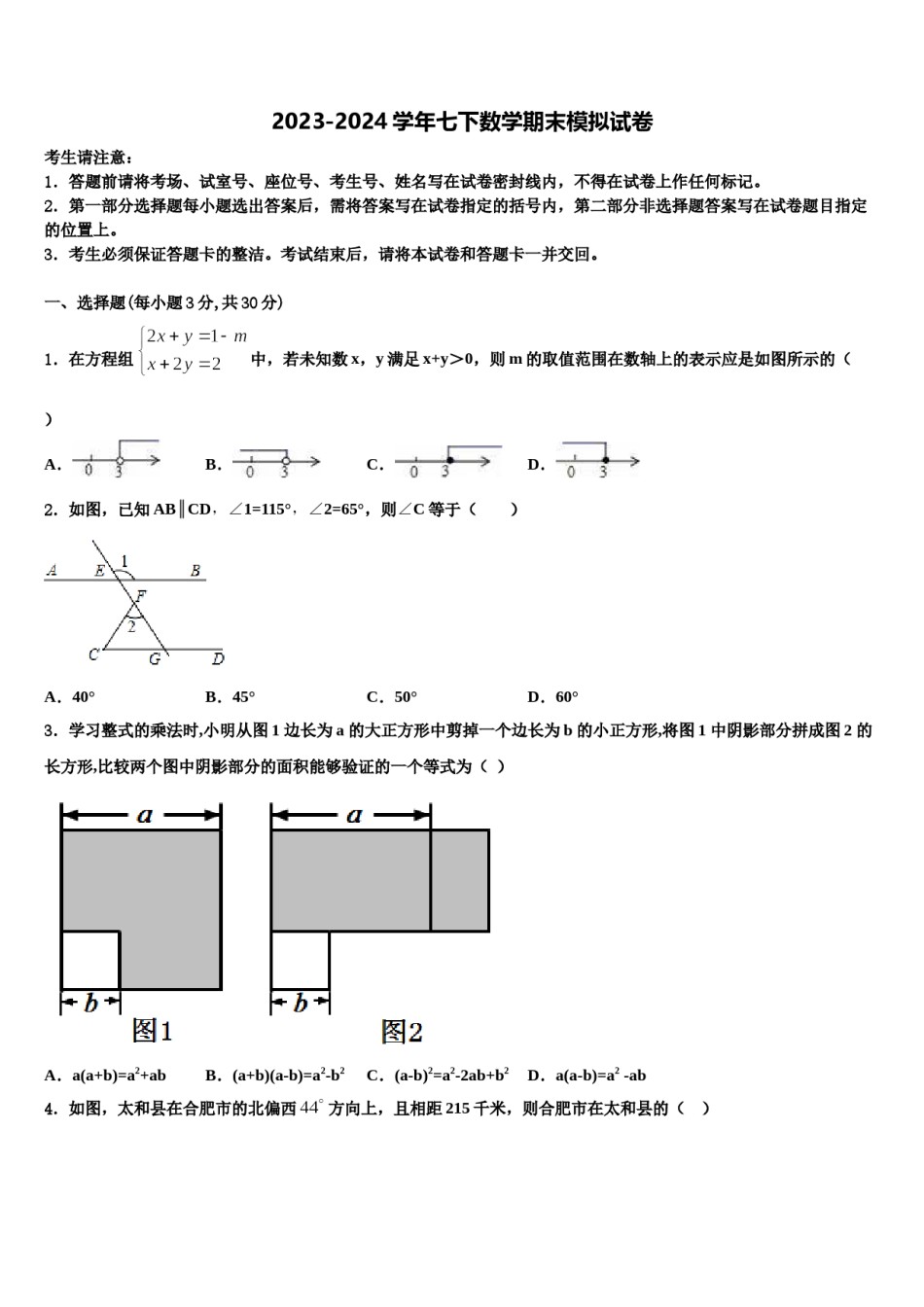
2023-2024学年七下数学期末模拟试卷考生请注意:1.答题前请将考场、试室号、座位号、考生号、姓名写在试卷密封线内,不得在试卷上作任何标记。2.第一部分选择题每小题选出答案后,需将答案写在试卷指定的括号内,第二部分非选择题答案写在试卷题目指定的位置上。3.考生必须保证答题卡的整洁。考试结束后,请将本试卷和答题卡一并交回。一、选择题(每小题3分,共30分)1.在方程组中,若未知数x,y满足x+y>0,则m的取值范围在数轴上的表示应是如图所示的()A.B.C.D.2.如图,已知AB∥CD,∠1=115°,∠2=65°,则∠C等于()A.40°B.45°C.50°D.60°3.学习整式的乘法时,小明从图1边长为a的大正方形中剪掉一个边长为b的小正方形,将图1中阴影部分拼成图2的长方形,比较两个图中阴影部分的面积能够验证的一个等式为()A.a(a+b)=a2+abB.(a+b)(a-b)=a2-b2C.(a-b)2=a2-2ab+b2D.a(a-b)=a2-ab4.如图,太和县在合肥市的北偏西方向上,且相距215千米,则合肥市在太和县的()A.南偏东方向上,相距215千米处B.南偏东方向上,相距215千米处C.南偏西方向上,相距215千米处D.南偏西方向上,相距215千米处5.确定一个地点的位置,下列说法正确的是()A.偏西50°,1000米B.东南方向,距此800米C.距此1000米D.正北方向6.16的平方根是()A.B.2C.D.47.将点A先向下平移3个单位长度,再向右平移4个单位长度,得到点A'(−3,−6),则点A的坐标为()A.(−7,3)B.(−7,−3)C.(6,−10)D.(−1,−10)8.点P(5,-3)所在的象限是()A.第一象限B.第二象限C.第三象限D.第四象限9.··100=()A.B.C.D.10.甲、乙两人从A地出发,沿同一方向练习跑步,如果甲让乙先跑10米,则甲跑5秒就可追上乙,如果甲让乙先跑2秒,那么甲跑4秒就能追上乙,设甲、乙每秒钟分别跑米和y米,则可列方程组为A.B.C.D.二、填空题(本大题共有6小题,每小题3分,共18分)11.平面直角坐标系中,点关于轴的对称点是__________.12.如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,AD是∠BAC的平分线.若P,Q分别是AD和AC上的动点,则PC+PQ的最小值是________;13.计算:=____________.14.如果把方程3x+y=2写成用含x的代数式表示y的形式,那么y=_____.15.分解因式:x2-1=______________.16.计算:___________________。三、解下列各题(本大题共8小题,共72分)17.(8分)如图1是一个五角星.(1)计算:∠A+∠B+∠C+∠D+∠E的度数.(2)当BE向上移动,过点A时,如图2,五个角的和(即∠CAD+∠B+∠C+∠D+∠E)有无变化?说明你的理由.(3)如图3,把图2中的点C向上移到BD上时,五个角的和(即∠CAD+∠B+∠ACE+∠D+∠E)有无变化?说明你的理由.18.(8分)(1)计算:;(2)解方程组:.19.(8分)如图,的顶点都在每个边长为l个单位长度的方格纸的格点上,将向右平移1格,再向上平移3格,得到.(1)请在图中画出;(1)的面积为________;(3)若AC的长约为1.8,试求AC边上的高为多少(结果保留分数)?20.(8分)分解因式(1);(2)21.(8分)阅读材料(1),并利用(1)的结论解决问题(2)和问题(3).(1)如图1,AB∥CD,E为形内一点,连结BE、DE得到∠BED,求证:∠E=∠B+∠D悦悦是这样做的:过点E作EF∥AB.则有∠BEF=∠B. AB∥CD,∴EF∥CD.∴∠FED=∠D.∴∠BEF+∠FED=∠B+∠D.即∠BED=∠B+∠D.(2)如图2,画出∠BEF和∠EFD的平分线,两线交于点G,猜想∠G的度数,并证明你的猜想.(3)如图3,EG1和EG2为∠BEF内满足∠1=∠2的两条线,分别与∠EFD的平分线交于点G1和G2,求证:∠FG1E+∠G2=180°.22.(10分)先化简(2x-1)2-(3x+1)(3x-1)+5x(x-1),再选取一个你喜欢的数代替x,并求原代数式的值.23.(10分)某市为提倡节约用水,准备实行自来水阶梯计算方式,用户用水不超出基本用水量的部分享受基本价格,超出基本用水量的部分实行加价收费,为了更好地决策,自来水公司随机抽取了部分用户的用水量数据,并绘制了如图不完整的统计图,(每组数据包括在右端点但不包括左端点),请你根据统计图解答下列问题:(1)此次抽样调查的...