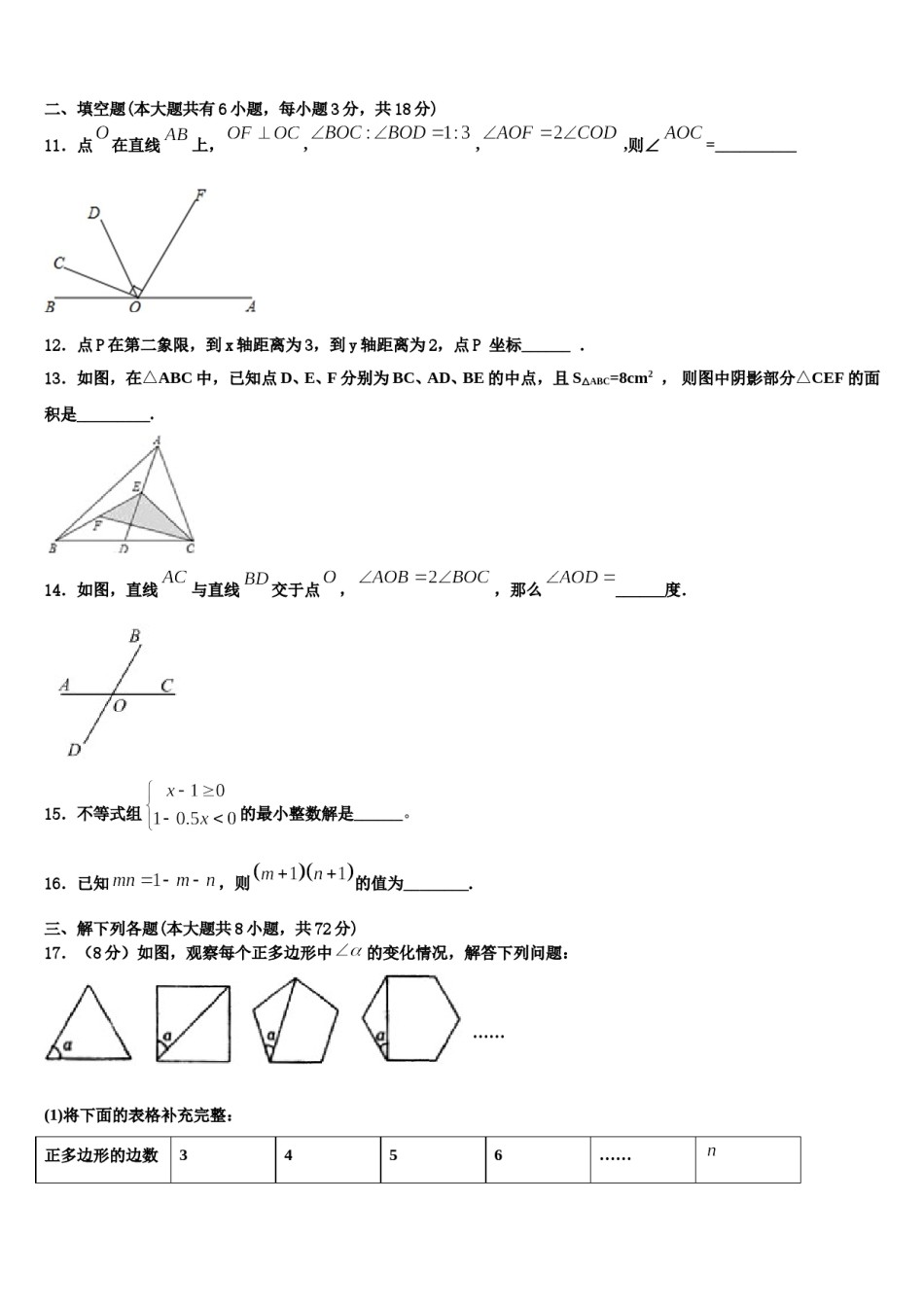
2023-2024学年七下数学期末模拟试卷注意事项:1.答题前,考生先将自己的姓名、准考证号填写清楚,将条形码准确粘贴在考生信息条形码粘贴区。2.选择题必须使用2B铅笔填涂;非选择题必须使用0.5毫米黑色字迹的签字笔书写,字体工整、笔迹清楚。3.请按照题号顺序在各题目的答题区域内作答,超出答题区域书写的答案无效;在草稿纸、试题卷上答题无效。4.保持卡面清洁,不要折叠,不要弄破、弄皱,不准使用涂改液、修正带、刮纸刀。一、选择题(每小题3分,共30分)1.雅安地震后,全国各地都有不少人士参与抗震救灾,家住成都的王伟也参加了,他要在规定时间内由成都赶到雅安.如果他以50千米/小时的速度行驶,就会迟到24分钟;如果以75千米/小时的高速行驶,则可提前24分钟到达.若设成都至雅安的路程为S,由成都到雅安的规定时间是t,则可得到方程组是()A.B.C.D.2.已知点,,点在轴的负半轴上,且的面积为,则点的坐标为()A.D.B.C.3.已知方程组的解也是方程3x-2y=0的解,则k的值是()A.k=-5B.k=5C.k=-10D.k=104.如图,能判断AB∥CD的条件是()A.∠1=∠4B.∠3=∠2C.∠3=∠1D.∠3=∠45.小明骑自行车上学,开始以正常速度匀速行驶,但行至中途时,自行车出了故障,只好停下来修车,车修好后,因怕耽误上课,他比修车前加快了速度继续匀速行驶,下面是行驶路程s(m)关于时间t(min)的函数图象,那么符合小明行驶情况的大致图象是()A.B.C.D.6.若点M的坐标为(b+2,),则下列说法正确的是()A.点M在x轴正半轴上B.点M在x轴负半轴上C.点M在y轴正半轴上D.点M在y轴负半轴上7.如图,在△ABC中,∠BAC=x,∠B=2x,∠C=3x,则∠BAD=()A.145°B.150°C.155°D.160°8.下列说法正确的是()A.任意掷一枚质地均匀的硬币10次,一定有5次正面向上B.“等腰三角形的一个角是80度,则它的顶角是80度”是必然事件C.“篮球队员在罚球线上投篮一次,投中”为随机事件D.“是有理数,”是不可能事件9.在平面直角坐标系中,点的坐标分别是,将三角形沿一确定方向平移得三角形,点的对应点的坐标是,则点坐标分别是()A.B.C.D.10.用不等式表示图中的解集,其中正确的是()A.x>-3B.x<-3C.x≥-3D.x≤-3二、填空题(本大题共有6小题,每小题3分,共18分)11.点在直线上,,,,则∠=__________12.点P在第二象限,到x轴距离为3,到y轴距离为2,点P坐标______.13.如图,在△ABC中,已知点D、E、F分别为BC、AD、BE的中点,且S△ABC=8cm2,则图中阴影部分△CEF的面积是_________.14.如图,直线与直线交于点,,那么______度.15.不等式组的最小整数解是______。16.已知,则的值为________.三、解下列各题(本大题共8小题,共72分)17.(8分)如图,观察每个正多边形中的变化情况,解答下列问题:……(1)将下面的表格补充完整:正多边形的边数3456……的度数____________________________________……_________(2)根据规律,是否存在一个正边形,使其中的?若存在,写出的值;若不存在,请说明理由.(3)根据规律,是否存在一个正边形,使其中的?若存在,写出的值;若不存在,请说明理由.18.(8分)将一个直角三角形纸板ABC放置在锐角△PMN上,使该直角三角形纸板的两条直角边AB,AC分别经过点M,N.(发现)(1)如图1,若点A在△PMN内,当∠P=30°时,则∠PMN+∠PNM=______°,∠AMN+∠ANM=______°,∠PMA+∠PNA=______°.(2)如图2,若点A在△PMN内,当∠P=50°时,∠PMA+∠PNA=______°.(探究)(3)若点A在△PMN内,请你判断∠PMA,∠PNA和∠P之间满足怎样的数量关系,并写出理由.(应用)(4)如图3,点A在△PMN内,过点P作直线EF∥AB,若∠PNA=16°,则∠NPE=______.19.(8分)如图,点A、B在数轴上且点A在点B的左侧,它们所对应的数分别是和.(1)当x=1.5时,求AB的长.(2)当点A到原点的距离比B到原点的距离多3,求x的值.20.(8分)七年级教师对试卷讲评课中学生参与的深度与广度进行评价调查,其评价项目为主动质疑、独立思考、专注听讲、讲解题目四项:评价组随机抽取了若干名初中学生的参与情况,绘制成如图所示的频数分布...