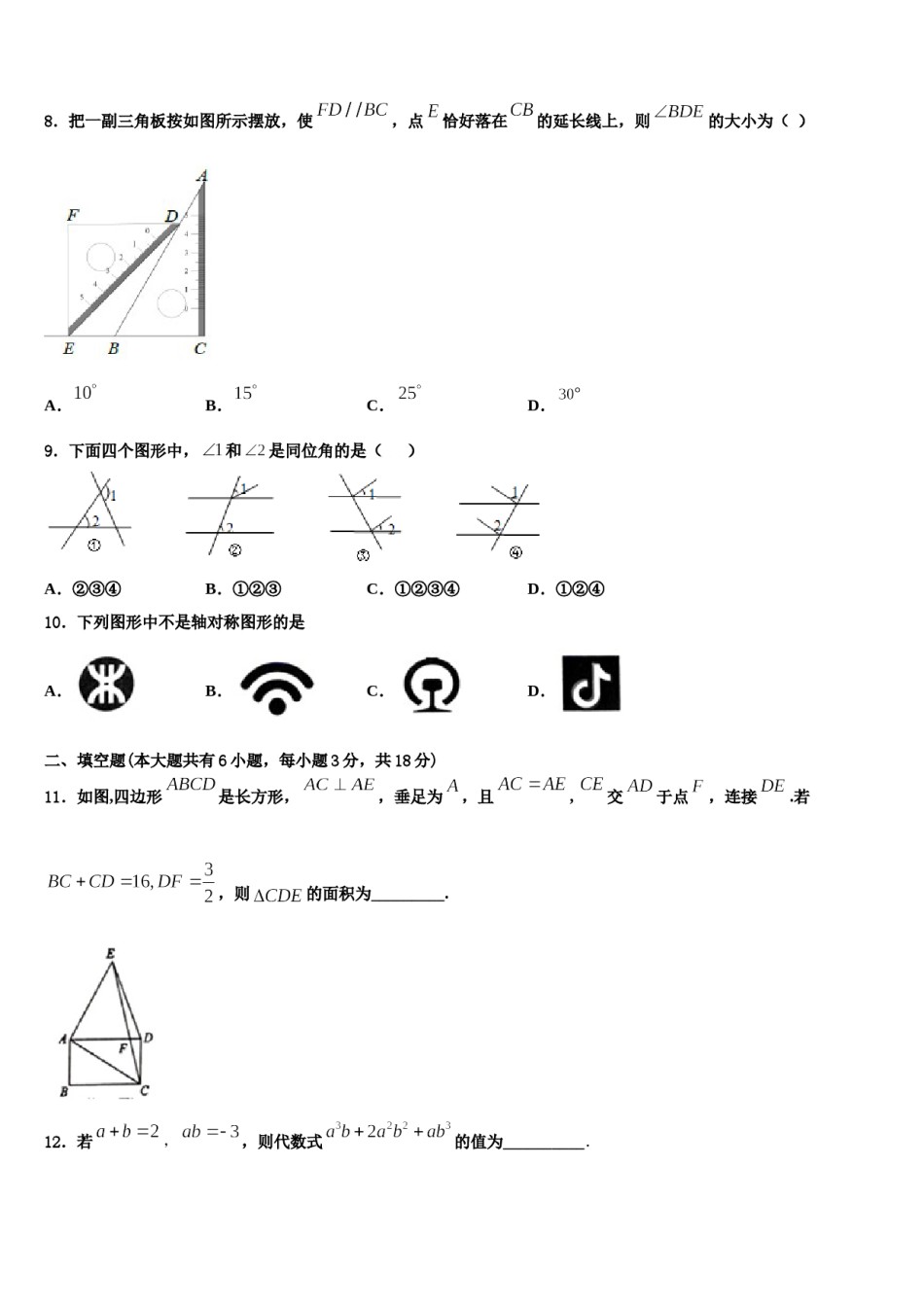
2023-2024学年七下数学期末模拟试卷考生须知:1.全卷分选择题和非选择题两部分,全部在答题纸上作答。选择题必须用2B铅笔填涂;非选择题的答案必须用黑色字迹的钢笔或答字笔写在“答题纸”相应位置上。2.请用黑色字迹的钢笔或答字笔在“答题纸”上先填写姓名和准考证号。3.保持卡面清洁,不要折叠,不要弄破、弄皱,在草稿纸、试题卷上答题无效。一、选择题(每小题3分,共30分)1.用三种正多边形铺设地板,其中两种是正方形和正五边形,则第三种正多边形的边数是()A.12B.15C.18D.202.下列调查中,适合用普查方法的是()A.了解中央电视台《中国诗词大会》的收视率B.了解太和县某学校初一(1)班学生的身高情况C.了解太和县出产的樱桃的含糖量D.调查某品牌笔芯的使用寿命3.若实数m满足1<m<2,则实数m可以是()A.B.C.D.﹣4.我国古代数学名著《孙子算经》中记载了一道题,大意是:100匹马恰好拉了100片瓦,已知1匹大马能拉3片瓦,3匹小马能拉1片瓦.问有多少匹大马、多少匹小马?若设大马有匹,小马有匹,那么可列方程组为()A.B.C.D.5.若关于的不等式组有两个整数解,则的取值范围是()A.B.C.D.6.单项式-的系数是()D.-3,则;③若A.7B.-7C.37.给出四个命题:①若,,则;②若,则;④若,则.真命题是()C.③D.④A.①B.②8.把一副三角板按如图所示摆放,使,点恰好落在的延长线上,则的大小为()A.B.C.D.9.下面四个图形中,和是同位角的是()A.②③④B.①②③C.①②③④D.①②④10.下列图形中不是轴对称图形的是A.B.C.D.二、填空题(本大题共有6小题,每小题3分,共18分)11.如图,四边形是长方形,,垂足为,且,交于点,连接.若,则的面积为_________.12.若,,则代数式的值为__________.13.如图,,的面积等于,,,则的面积是_______.14.如图,在中,D是BC延长线上一点,,,则__________.15.如图,将沿BC方向平移得到,若,,,,,阴影部分的面积为______.16.若,则的值是______.三、解下列各题(本大题共8小题,共72分)17.(8分)解不等式(组),并把解集在数轴上表示出来(1)(2)18.(8分)证明:两个连续偶数的平方差一定是的倍数19.(8分)王老师在黑板上写下了四个算式:①32-12=(3+1)(3-1)=8=8×1,②52-32=(5+3)(5-3)=16=8×2,③72-52=(7+5)(7-5)=21=8×3,④92-72=(9+7)(9-7)=32=8×1.…认真观察这些算式,并结合你发现的规律,解答下列问题:(1)请再写出另外两个符合规律的算式:算式①______;算式②______.(2)小华发现上述算式的规律可以用文字语言概括为:“两个连续奇数的平方差能被8整除”,如果设两个连续奇数分别为2n+1和2n-1(n为正整数),请你用含有n的算式验证小华发现的规律.20.(8分)在△ABC中,∠C=90°,∠BAC=60°,△ABC绕点C顺时针旋转,旋转角为α(0°<α<180°),点A、B的对应点分别是点D、E.(1)如图1,当点D恰好落在边AB上时,试判断DE与AC的位置关系,并说明理由.(2)如图2,当点B、D、E三点恰好在一直线上时,旋转角α=__°,此时直线CE与AB的位置关系是__.(3)在(2)的条件下,联结AE,设△BDC的面积S1,△AEC的面积S2,则S1与S2的数量关系是_____.(4)如图3,当点B、D、E三点不在一直线上时,(3)中的S1与S2的数量关系仍然成立吗?试说明理由.21.(8分)(1)计算:;(2)因式分解:.22.(10分)分解因式:23.(10分)如图,在方格纸内将水平向右平移4个单位得到△.(1)画出△;(2)画出边上的中线和高线;(利用网格点和直尺画图)(3)的面积为.24.(12分)一个正方形在平面直角坐标系内的位置如图所示,已知点A的坐标为(3,0),线段AC与BD的交点是M.(1)写出点M、B、C、D的坐标;(2)当正方形中的点M由现在的位置经过平移后,得到点M(﹣4,6)时,写出点A、B、C、D的对应点A′、B′、C′、D′的坐标,并求出四边形A′B′C′D′的面积参考答案一、选择题(每小题3分,共30分)1、D【解析】根据正方形和正五边形的内角度数以及拼成一个圆周角,求出正多边的一个内角,从而判断正多边形的边数.【详解】正方形和正五边...