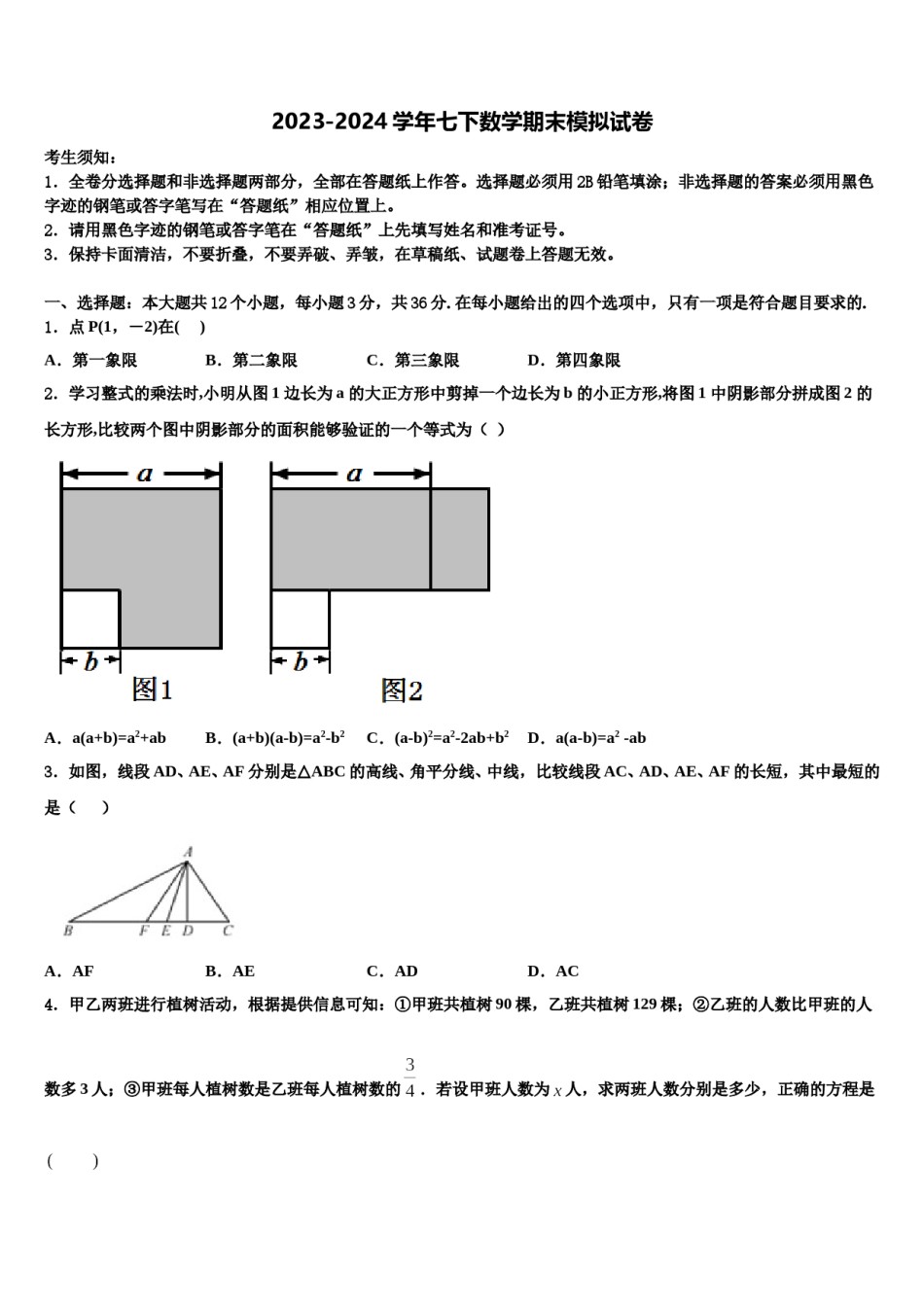
2023-2024学年七下数学期末模拟试卷考生须知:1.全卷分选择题和非选择题两部分,全部在答题纸上作答。选择题必须用2B铅笔填涂;非选择题的答案必须用黑色字迹的钢笔或答字笔写在“答题纸”相应位置上。2.请用黑色字迹的钢笔或答字笔在“答题纸”上先填写姓名和准考证号。3.保持卡面清洁,不要折叠,不要弄破、弄皱,在草稿纸、试题卷上答题无效。一、选择题:本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.点P(1,-2)在()A.第一象限B.第二象限C.第三象限D.第四象限2.学习整式的乘法时,小明从图1边长为a的大正方形中剪掉一个边长为b的小正方形,将图1中阴影部分拼成图2的长方形,比较两个图中阴影部分的面积能够验证的一个等式为()A.a(a+b)=a2+abB.(a+b)(a-b)=a2-b2C.(a-b)2=a2-2ab+b2D.a(a-b)=a2-ab3.如图,线段AD、AE、AF分别是△ABC的高线、角平分线、中线,比较线段AC、AD、AE、AF的长短,其中最短的是()A.AFB.AEC.ADD.AC4.甲乙两班进行植树活动,根据提供信息可知:①甲班共植树90棵,乙班共植树129棵;②乙班的人数比甲班的人数多3人;③甲班每人植树数是乙班每人植树数的.若设甲班人数为人,求两班人数分别是多少,正确的方程是A.B.C.D.5.如果a,b表示两个负数,且a>b,则()A.>1B.C.D.ab<06.不等式组的整数解是()A.-1,0,1B.0,1C.-2,0,1D.-1,17.古希腊著名的毕达哥拉斯学派把1,3,6,10,…这样的数称为“三角形数”,而把1,4,9,16,…这样的数称为“正方形数”.从图中可以发现,任何一个大于1的“正方形数”都可以看作两个相邻“三角形数”之和.下列等式中,符合这一规律的是()A.9=4+5B.C.D.8.△ABC的两边分别为方程组的解,第三边能被4整除.这样的三角形有()个A.1B.2C.3D.49.王老师的数学课采用小组合作学习方式,把班上40名学生分成若干小组,如果要求每小组只能是5人或6人,则有几种分组方案B.3C.2D.1A.410.一只小狗在如图的方砖上走来走去,若最终停在阴影方砖上,则甲胜,否则乙胜,那么甲的获胜概率是()A.B.C.D.11.如图,将三角形纸板ABC沿直线AB向右平行移动,使∠A到达∠B的位置,若∠CAB=45°,∠ABC=100°,则∠CBE的度数为()A.25°B.30°C.35°D.40°12.如图,已知△ABC,求作一点P,使P到∠A的两边的距离相等,且PA=PB、下列确定P点的方法正确的是()A.P为∠A、∠B两角平分线的交点B.P为AC、AB两边上的高的交点C.P为∠A的角平分线与AB的垂直平分线的交点D.P为AC、AB两边的垂直平分线的交点二、填空题(每题4分,满分20分,将答案填在答题纸上)13.如图,在中,、的角平分线相交于点,若,则______°14.不等式2x+9≥3(x+2)的正整数解是__________.15.如图,有个圆,,,,且圆与圆的半径之和等于圆的半径,圆与圆的半径之和等于圆的半径,现将圆,,摆放如图甲,圆,,摆放如图乙.若图甲和图乙的阴影部分面积分别为和.则圆面积为__________.16.如图,将一个宽度相等的纸条沿AB折叠一下,如果∠1=130º,那么∠2=.17.写出a3b2c的一个同类项:▲.三、解答题(本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)18.(5分)沙坪坝区2017年已经成功创建国家卫生城区,现在正全力争创全国文明城区(简称“创文”),某街道积极响应“创文”活动,投入一定资金用于绿化一块闲置空地,购买了甲、乙两种树木共72棵,其中甲种树木每棵90元,乙种树木每棵80元,共用去资金6160元.(1)求甲、乙两种树木各购买了多少棵?(2)经过一段时间后,种植的这批树木成活率高,绿化效果好,该街道决定再购买一批这两种树木绿化另一块闲置空地,两种树木的购买数量均与第一批相同,购买时发现甲种树木单价上涨了,乙种树木单价下降了,且总费用不超过6804元,求的最大值.19.(5分)请填写推理的依据和解题过程.如图所示,,,,垂足分别为点、,求证:.证明:,(已知),,,)(_________________________.()又(已知),_________________(等量代换),()20.(8分)如图所示,三角形(记作)在方格中,方格...