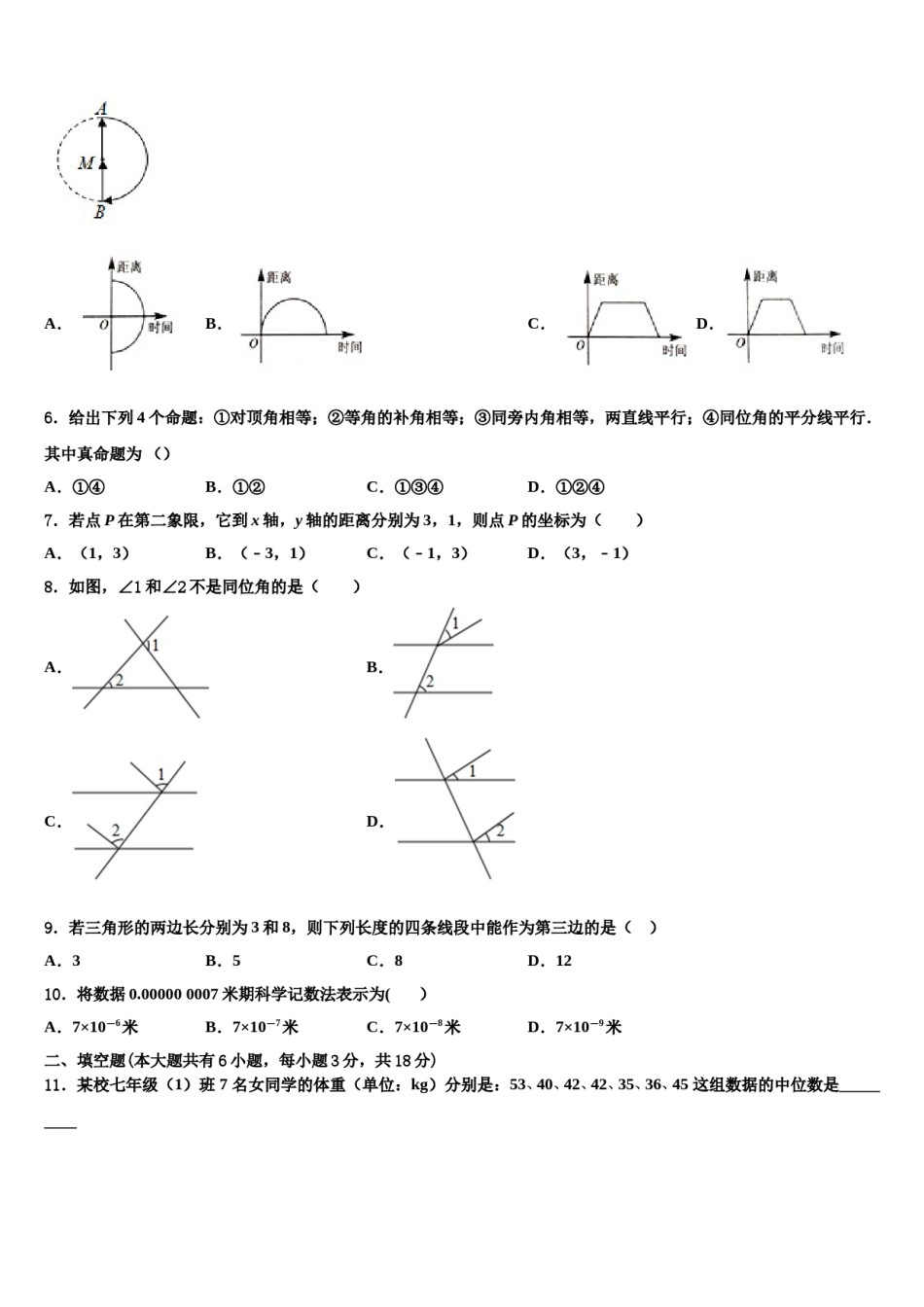
2023-2024学年七下数学期末模拟试卷考生须知:1.全卷分选择题和非选择题两部分,全部在答题纸上作答。选择题必须用2B铅笔填涂;非选择题的答案必须用黑色字迹的钢笔或答字笔写在“答题纸”相应位置上。2.请用黑色字迹的钢笔或答字笔在“答题纸”上先填写姓名和准考证号。3.保持卡面清洁,不要折叠,不要弄破、弄皱,在草稿纸、试题卷上答题无效。一、选择题(每小题3分,共30分)1.如图,动点P在平面直角坐标系中按图中箭头所示方向运动,第1次从原点运动到点(1,1),第2次接着运动到点(2,0),第3次接着运动到点(3,2),…,按这样的运动规律,经过第2019次运动后,动点P的坐标是()A.(2018,0)B.(2018,2)C.(2019,2)D.(2019,0)2.下面式子从左边到右边的变形是因式分解的是()A.x2﹣x﹣2=x(x﹣1)﹣2B.x2﹣4x+4=(x﹣2)2C.(x+1)(x﹣1)=x2﹣1D.x﹣1=x(1﹣)3.不等式3x-2>1的解集在数轴上表示正确的是()A.B.C.D.4.P(m,n)是第二象限内一点,则P′(m﹣2,n+1)位于()D.第四象限A.第一象限B.第二象限C.第三象限5.如图,小明在操场上匀速散步,某一段时间内先从点出发到点,再从点沿半圆弧到点,最后从点回到点,能近似刻画小明到出发点的距离与时间之间的关系的图像是()A.B.C.D.6.给出下列4个命题:①对顶角相等;②等角的补角相等;③同旁内角相等,两直线平行;④同位角的平分线平行.其中真命题为()A.①④B.①②C.①③④D.①②④7.若点P在第二象限,它到x轴,y轴的距离分别为3,1,则点P的坐标为()A.(1,3)B.(﹣3,1)C.(﹣1,3)D.(3,﹣1)8.如图,∠1和∠2不是同位角的是()A.B.C.D.9.若三角形的两边长分别为3和8,则下列长度的四条线段中能作为第三边的是()A.3B.5C.8D.1210.将数据0.000000007米期科学记数法表示为()A.7×10-6米B.7×10-7米C.7×10-8米D.7×10-9米二、填空题(本大题共有6小题,每小题3分,共18分)11.某校七年级(1)班7名女同学的体重(单位:kg)分别是:53、40、42、42、35、36、45这组数据的中位数是_________12.若方程有增根,则的值为____.13.如图,△A′B′C′是由△ABC沿射线AC方向平移2cm得到,若AC=3cm,则A′C=cm.14.《九章算术》是中国传统数学最重要的著作,奠定了中国传统数学的基本框架.其中第七卷《盈不足》记载了一道有趣的数学问题:“今有大器五、小器一容三斛;大器一、小器五容二斛.问大、小器各容几何?”译文:“今有大容器5个,小容器1个,总容量为3斛;大容器1个,小容器5个,总容量为2斛.问大容器、小容器的容积各是多少斛?”设大容器的容积为斛,小容器的容积为斛,根据题意,可列方程组为_____________________.15.规定符号⊗的意义为:a⊗b=ab﹣a﹣b+1,那么﹣2⊗5=_____.16.++﹣1=_____.三、解下列各题(本大题共8小题,共72分)17.(8分)方程mx+ny=1的两个解是,,求m和n的值.18.(8分)解方程(组):(1)(2)19.(8分)解不等式,并把解集表示在数轴上.20.(8分)如图,四边形ABCD中,AD∥BC,∠ABC=90°.(1)直接填空:∠BAD=______°.(2)点P在CD上,连结AP,AM平分∠DAP,AN平分∠PAB,AM、AN分别与射线BP交于点M、N.设∠DAM=α°.①求∠BAN的度数(用含α的代数式表示).②若AN⊥BM,试探究∠AMB的度数是否为定值?若为定值,请求出该定值;若不为定值,请用α的代数式表示它.21.(8分)如图,已知AB∥CD,∠B=60°,CM平分∠ECB,∠MCN=90°,求∠DCN的度数.22.(10分)如图,将绕着点B顺时针旋转至,使得C点落在AB的延长线上的D点处,的边BC恰好是的角平分线.(1)试求旋转角的度数;(2)设BE与AC的交点为点P,求证:.23.(10分)问题情境:如图1,,,,求的度数.小明的思路是过点作,通过平行线性质来求.(1)按照小明的思路,写出推算过程,求的度数.(2)问题迁移:如图2,,点在射线上运动,记,,当点在、两点之间运动时,问与、之间有何数量关系?请说明理由.(3)在(2)的条件下,当点在线段上时,请直接写出与、之间的数量关系.24.(12分)请阅读下面的诗句:“栖...