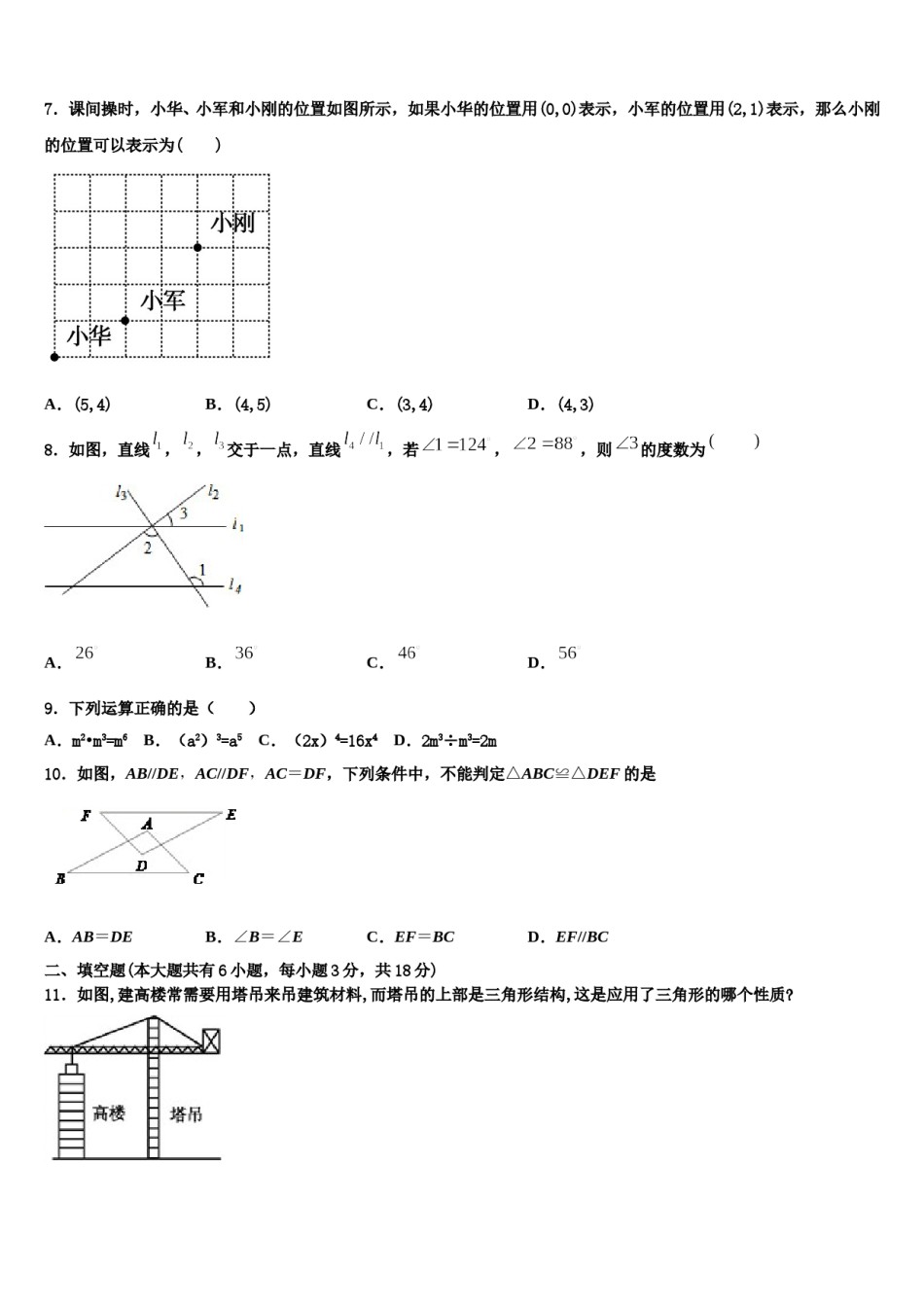
2023-2024学年七下数学期末模拟试卷注意事项:1.答题前,考生先将自己的姓名、准考证号码填写清楚,将条形码准确粘贴在条形码区域内。2.答题时请按要求用笔。3.请按照题号顺序在答题卡各题目的答题区域内作答,超出答题区域书写的答案无效;在草稿纸、试卷上答题无效。4.作图可先使用铅笔画出,确定后必须用黑色字迹的签字笔描黑。5.保持卡面清洁,不要折暴、不要弄破、弄皱,不准使用涂改液、修正带、刮纸刀。一、选择题(每小题3分,共30分)1.下列图形中,由∠1=∠2≠90°,能得到AB∥CD的是()A.B.C.D.2.有一个数值转换器,原理如下:当输入的x=4时,输出的y等于()A.-B.C.2D.43.如果方程组的解为,那么其中的m,n代表的两个数分别为A.10,4B.4,10C.3,10D.10,34.下列运算结果为的是()A.B.C.D.5.若点(2,6),点(-3,6),那么点、所在的直线是()A.直线;B.直线;C.直线;D.直线.6.若m>n,则下列不等式不成立的是()A.m-2>n-2B.3-m>3-nC.m+3a>n+3aD.7.课间操时,小华、小军和小刚的位置如图所示,如果小华的位置用(0,0)表示,小军的位置用(2,1)表示,那么小刚的位置可以表示为()A.(5,4)B.(4,5)C.(3,4)D.(4,3)8.如图,直线,,交于一点,直线,若,,则的度数为A.B.C.D.9.下列运算正确的是()A.m2•m3=m6B.(a2)3=a5C.(2x)4=16x4D.2m3÷m3=2m10.如图,AB//DE,AC//DF,AC=DF,下列条件中,不能判定△ABC≌△DEF的是A.AB=DEB.∠B=∠EC.EF=BCD.EF//BC二、填空题(本大题共有6小题,每小题3分,共18分)11.如图,建高楼常需要用塔吊来吊建筑材料,而塔吊的上部是三角形结构,这是应用了三角形的哪个性质?答:______.12.小明、小辉两家所在位置关于学校中心对称.如果小明家距学校2公里,那么他们两家相距__________公里.13.如图,直线相交于点,,那么__________________________。14.如图,将直径为1个单位长度的圆从原点处沿着数轴无滑动的逆时针滚动一周,使圆上的点A从原点运动至数轴上的点B,则点B表示的数是_______.15.当x=____时,代数式4x-5与3x-6的值互为相反.16.已知a,b,c是△ABC的三边长,a,b满足a﹣7+(b﹣1)2=0,c为奇数,则c=_____.三、解下列各题(本大题共8小题,共72分)17.(8分)甲、乙两人共同解方程组,由于甲看错了方程①中的a,得到方程组的解为;乙看错了方程②中的b,得到方程组的解为,试计算a2018+(﹣b)2017的值.18.(8分)解不等式组:并写出它的所有整数解.19.(8分)小明某天上午9时骑自行车离开家,15时回家,他有意描绘了离家的距离与时间的变化情况(如图所示).(1)图象表示了哪两个变量的关系?(2)10时,他离家多远?(3)他到达离家最远的地方是什么时间?离家多远?(4)他可能在哪段时间内休息,并吃午餐?(5)他由离家最远的地方返回时的平均速度是多少?20.(8分)某校积极推进“阳光体育”工程,本学期在九年级11个班中开展篮球单循环比赛(每个班与其它班分别进行一场比赛,每班需进行10场比赛).比赛规则规定:每场比赛都要分出胜负,胜一场得3分,负一场得﹣1分.(1)如果某班在所有的比赛中只得14分,那么该班胜负场数分别是多少?(2)假设比赛结束后,甲班得分是乙班的3倍,甲班获胜的场数不超过5场,且甲班获胜的场数多于乙班,请你求出甲班、乙班各胜了几场.21.(8分)在数学课本中,有这样一道题:已知:如(图1),∠B+∠C=∠BEC求证:AB∥CD(1)请补充下面证明过程证明:过点E,做EF∥AB,如(图2)∴∠B=∠ ∠B+∠C=∠BEC∠BEF+∠FEC=∠BEC(已知)∴∠B+∠C=∠BEF+∠FEC(等量代换)∴∠=∠(等式性质)∴EF∥ EF∥AB∴AB∥CD(平行于同一条直线的两条直线互相平行)(2)请再选用一种方法,加以证明22.(10分)阅读理解:求代数式x2+1x+8的最小值.解:因为x2+1x+8=(x2+1x+1)+1=(x+2)2+1≥1,所以当x=﹣2时,代数式x2+1x+8有最小值,最小值是1.仿照上述解题过程求值.(1)应用:求代数式m2+2m+3的最小值.(2)拓展:求代数式﹣m2+3m+的最大值.23.(10分)如图,已知在每个小正方形边长为1的网格图形中,...