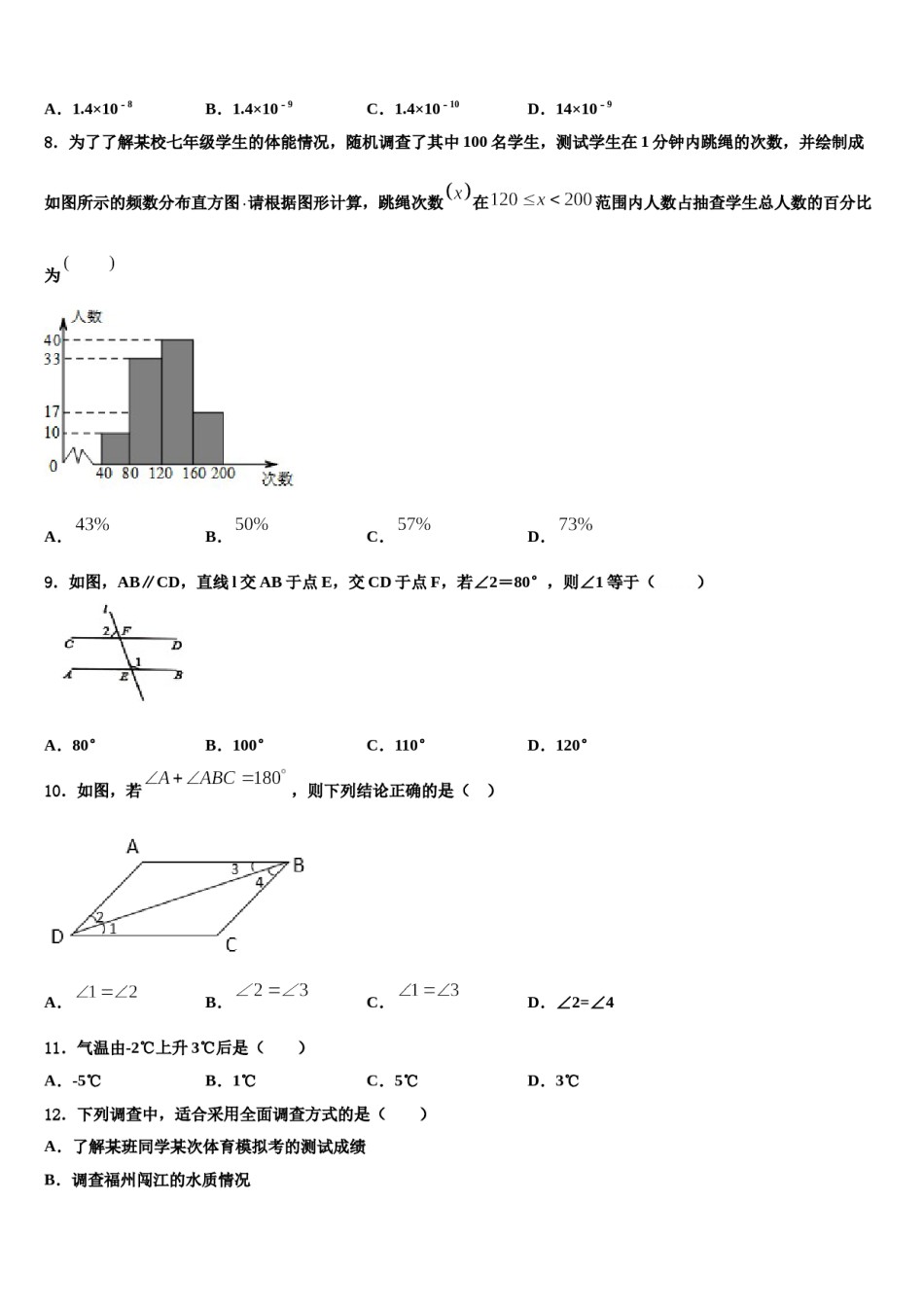
2023-2024学年七下数学期末模拟试卷考生须知:1.全卷分选择题和非选择题两部分,全部在答题纸上作答。选择题必须用2B铅笔填涂;非选择题的答案必须用黑色字迹的钢笔或答字笔写在“答题纸”相应位置上。2.请用黑色字迹的钢笔或答字笔在“答题纸”上先填写姓名和准考证号。3.保持卡面清洁,不要折叠,不要弄破、弄皱,在草稿纸、试题卷上答题无效。一、选择题:本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.计算(﹣1)﹣2018+(﹣1)2017所得的结果是()A.﹣1B.0C.1D.﹣22.下列图形中,线段MN的长度表示点M到直线l的距离的是()A.B.C.D.3.下列命题中,假命题是()A.如果两条直线都与第三条直线平行,那么这两条直线也互相平行B.在同一平面内,过一点有且只有一条直线与已知直线垂直C.两条直线被第三条直线所截,同旁内角互补D.两直线平行,内错角相等4.为了测算一块600亩试验田里新培育的杂交水稻的产量,随机对其中的50亩杂交水稻的产量进行了检测,在这个问题中,数字50是()A.个体B.总体C.样本容量D.总体的样本5.已知,则代数式的值为()A.2B.1C.0D.-16.如图,直线与直线相交,将直线沿的方向平移得到直线,若,则的度数为()A.B.C.D.7.芯片是手机、电脑等高科技产品最核心的部件,更小的芯片意味着更高的性能.目前我国芯片的量产工艺已达到14纳米,已知14纳米为0.000000014米,则0.000000014科学记数法表示为()A.1.4×10﹣8B.1.4×10﹣9C.1.4×10﹣10D.14×10﹣98.为了了解某校七年级学生的体能情况,随机调查了其中100名学生,测试学生在1分钟内跳绳的次数,并绘制成如图所示的频数分布直方图请根据图形计算,跳绳次数在范围内人数占抽查学生总人数的百分比为A.B.C.D.9.如图,AB∥CD,直线l交AB于点E,交CD于点F,若∠2=80°,则∠1等于()A.80°B.100°C.110°D.120°10.如图,若,则下列结论正确的是()A.B.C.D.∠2=∠4D.3℃11.气温由-2℃上升3℃后是()A.-5℃B.1℃C.5℃12.下列调查中,适合采用全面调查方式的是()A.了解某班同学某次体育模拟考的测试成绩B.调查福州闯江的水质情况C.调查“中国诗词大会”的收视率D.调查某批次汽车的抗撞击能力二、填空题(每题4分,满分20分,将答案填在答题纸上)13.如图折叠一张矩形纸片,已知∠1=70°,则∠2的度数是__.14.不等式﹣3x+10>0的正整数解有_________.15.,,则__________.16.如图中的四边形均为长方形,根据图形,写出一个正确的等式:_____.17.若,则_____.三、解答题(本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)18.(5分)已知关于,的二元一次方程组的解满足,求满足条件的的所有非负整数值.19.(5分)如图,在正方形网格上有一个△ABC,作△ABC关于直线MN的对称图形(不写作法).20.(8分)阅读理(解析)提出问题:如图1,在四边形ABCD中,P是AD边上任意一点,△PBC与△ABC和△DBC的面积之间有什么关系?探究发现:为了解决这个问题,我们可以先从一些简单的、特殊的情形入手:当AP=AD时(如图2): AP=AD,△ABP和△ABD的高相等,∴S△ABP=S△ABD, PD=AD﹣AP=AD,△CDP和△CDA的高相等∴S△CDP=S△CDA,∴S△PBC=S四边形ABCD﹣S△ABP﹣S△CDP=S四边形﹣ABCDS△ABD﹣S△CDA,=S四边形﹣ABCD(S四边形ABCD﹣S△DBC)﹣(S四边形ABCD﹣S△ABC)=S△DBC+S△ABC.(1)当AP=AD时,探求S△PBC与S△ABC和S△DBC之间的关系式并证明;(2)当AP=AD时,S△PBC与S△ABC和S△DBC之间的关系式为:;(3)一般地,当AP=AD(n表示正整数)时,探求S△PBC与S△ABC和S△DBC之间的关系为:;(4)当AP=AD(0≤≤1)时,S△PBC与S△ABC和S△DBC之间的关系式为:.21.(10分)计算:(1)(2)(x-3)(2x+5)22.(10分)如图1,△CEF的顶点C、E、F分别与正方形ABCD的顶点C、A、B重合.(1)若正方形的边长为,用含的代数式表示:正方形ABCD的周长等于,△CEF的面积等于.(2)如图2,将△CEF绕点A顺时针旋转,边CE和正方形的边AD交于点P.连结AE,设旋转角∠BCF=β...