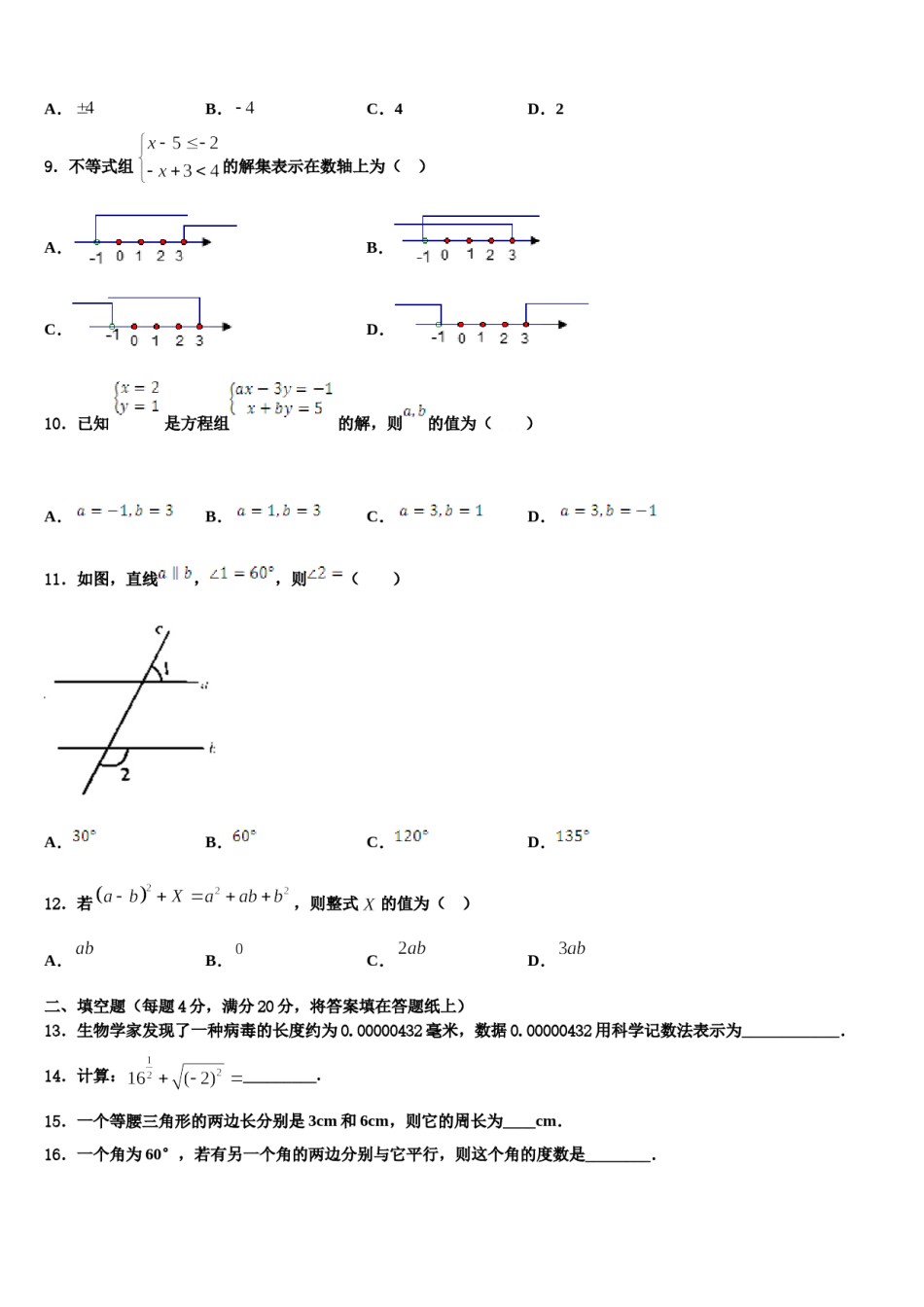
2023-2024学年七下数学期末模拟试卷考生须知:1.全卷分选择题和非选择题两部分,全部在答题纸上作答。选择题必须用2B铅笔填涂;非选择题的答案必须用黑色字迹的钢笔或答字笔写在“答题纸”相应位置上。2.请用黑色字迹的钢笔或答字笔在“答题纸”上先填写姓名和准考证号。3.保持卡面清洁,不要折叠,不要弄破、弄皱,在草稿纸、试题卷上答题无效。一、选择题:本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.如图,能够判定AD∥BC的是()A.∠1=∠3B.∠B=∠DC.∠2=∠4D.∠B+∠BCD=1802.若mn,则下列不等式中,正确的是()A.mnB.C.mnD.2mn3.方程3x+y=7的正整数解有()A.1组B.2组C.3组D.无数值4.下列命题正确的是()A.若a>b,b<c,则a>cB.若a∥b,b∥c,则a∥cC.49的平方根是7D.负数没有立方根5.下列调查,比较适合全面调查(普查)方式的是()A.调查端午期间市场上的粽子质量情况B.调查长江流域水污染情况C.调查某品牌圆珠笔笔芯的使用寿命D.调查乘坐飞机的旅客是否携带了违禁物品6.若m<n,则下列各式正确的是()A.2m>2nB.m﹣2>n﹣2C.﹣3m>﹣3nD.>7.若关于的不等式组无解,则的取值范围是()A.B.C.D.8.等于()A.B.C.4D.29.不等式组A.的解集表示在数轴上为()C.B.D.10.已知是方程组的解,则的值为()A.B.C.D.11.如图,直线,,则()A.B.C.D.12.若,则整式的值为()A.B.C.D.二、填空题(每题4分,满分20分,将答案填在答题纸上)13.生物学家发现了一种病毒的长度约为0.00000432毫米,数据0.00000432用科学记数法表示为____________.14.计算:_________.15.一个等腰三角形的两边长分别是3cm和6cm,则它的周长为____cm.16.一个角为60°,若有另一个角的两边分别与它平行,则这个角的度数是________.17.如图,已知直角三角形ABC中,∠C=90°,将△ABC绕点A逆时针旋转至△AED,使点C的对应点D恰好落在边AB上,E为点B的对应点.设∠BAC=a,则∠BED=_____.(用含a的代数式表示)三、解答题(本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)18.(5分)如图,Rt△ABC中,∠ACB=90°,斜边AB边上的高CD与角平分线AE交于点F,经过垂足D的直线分别交直线CA,BC于点M,N.(1)若AC=3,BC=4,AB=5,求CD的长;(2)当∠AMN=32°,∠B=38°时,求∠MDB的度数;(3)当∠AMN=∠BDN时,写出图中所有与∠CDN相等的角,并选择其中一组进行证明.19.(5分)如图,已知DE是AC的垂直平分线,AB=10cm,BC=11cm,则△ABD的周长为__cm.20.(8分)某汽车销售公司经销某品牌A、B两款汽车,已知A款汽车每辆进价为万元,B款汽车每辆进价为6万元.公司预计用不多于135万元且不少于129万元的资金购进这两款汽车共20辆,有几种进货方案,它们分别是什么?如果A款汽车每辆售价为9万元,B款汽车每辆售价为8万元,为打开B款汽车的销路,公司决定每售出一辆B款汽车,返还顾客现金a万元,要使中所有的方案获利相同,a值应是多少,此种方案是什么?(提示:可设购进B款汽车x辆)21.(10分)如图,将△ABC绕点C顺时针旋转90°得到△EDC.若点A、D、E在同一条直线上,且∠ACB=20°,求∠CAE及∠B的度数.22.(10分)在平面直角坐标系xOy中,对于P,Q两点给出如下定义:若点P到x,y轴的距离中的最大值等于点Q到x,y轴的距离中的最大值,则称P,Q两点为“等距点”图中的P,Q两点即为“等距点”.(1)已知点A的坐标为.①在点中,为点A的“等距点”的是________;②若点B的坐标为,且A,B两点为“等距点”,则点B的坐标为________.(2)若两点为“等距点”,求k的值.23.(12分)如图,在中,点、是与三等分线的交点,连接(1)求证:平分;的度数.(2)若,求参考答案一、选择题:本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.1、C【解析】根据内错角相等,两直线平行,即可得到正确结论.【详解】解:根据∠2=∠4,可得AD∥BC;根据∠B=∠D,不能得到AD∥BC;根据∠1=∠3,可得AB∥CD,不能得到AD∥BC;根据∠...