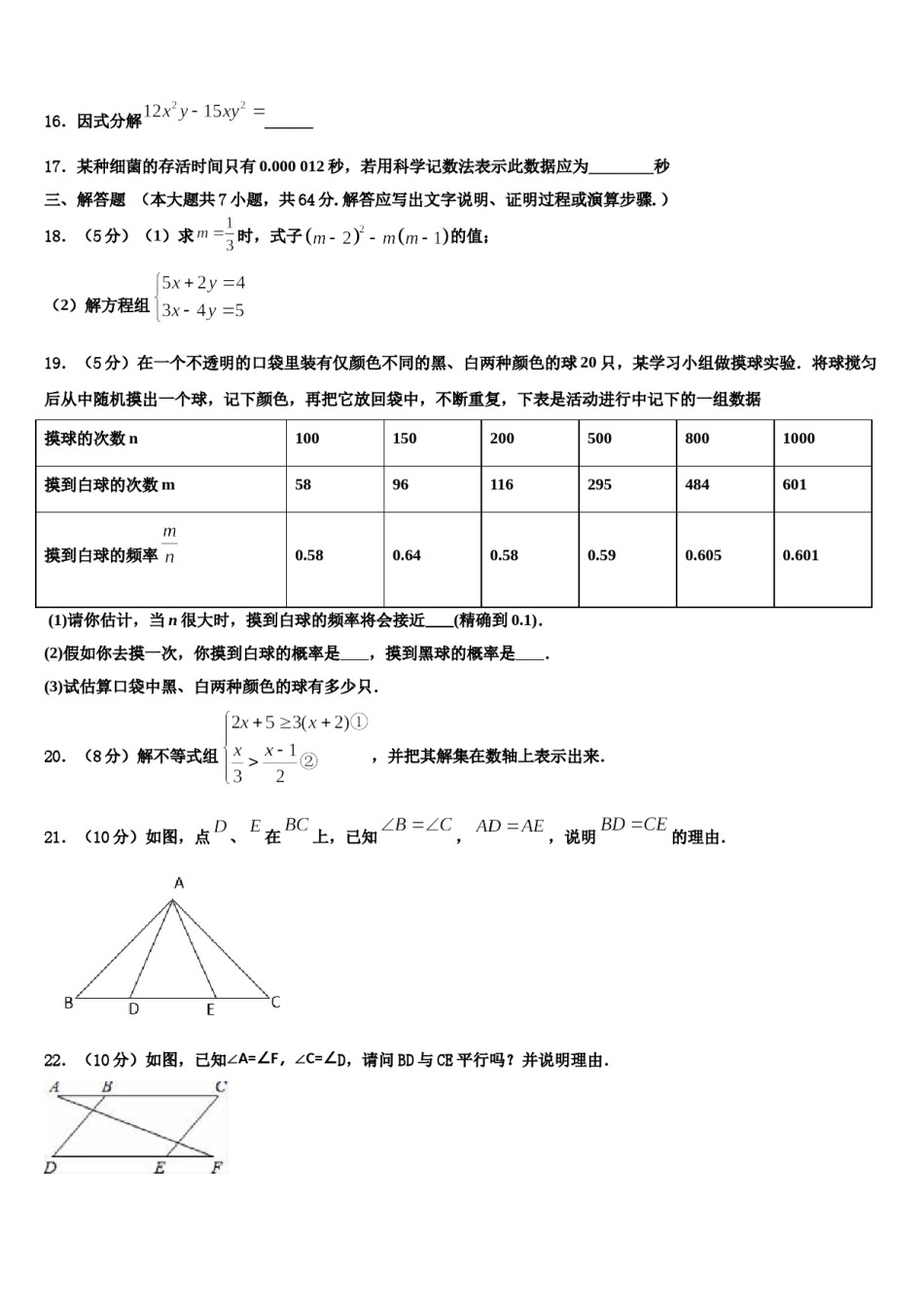
2023-2024学年七下数学期末模拟试卷考生须知:1.全卷分选择题和非选择题两部分,全部在答题纸上作答。选择题必须用2B铅笔填涂;非选择题的答案必须用黑色字迹的钢笔或答字笔写在“答题纸”相应位置上。2.请用黑色字迹的钢笔或答字笔在“答题纸”上先填写姓名和准考证号。3.保持卡面清洁,不要折叠,不要弄破、弄皱,在草稿纸、试题卷上答题无效。一、选择题:本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.下列式子中,正确的是()A.B.C.D.2.关于字母的多项式化简后不含项,则为()A.B.C.D.3.如果一个三角形的三边、、,满足,那么这个三角形一定是()A.等边三角形B.等腰三角形C.不等边三角形D.直角三角形4.已知一个三角形的两边长分别为2、5,则第三边的长可以为()A.2B.3C.5D.75.某次知识竞赛共有20道题,每答对一道题得10分,答错或不答都扣5分.娜娜得分要超过90分,设她答对了x道题,则根据题意可列不等式为()B.10x-5(20-x)>90A.10x-5(20-x)≥90D.20×10-5x≥90C.20×10-5x>906.若,则下列选项不正确的是()A.B.C.D.7.下列说法中,不正确的是()A.两直线相交所成的四个角中有两个角相等,则这两条直线互相垂直B.在同一平面内,经过一已知点能画一条直线和已知直线垂直C.一条直线可以有无数条垂线D.在同一平面内,过射线的端点与射线垂直的直线只有一条8.如果(x-2)(x+3)=x2+px+q,那么p、q的值是()A.p=5,q=6B.p=1,q=-6C.p=1,q=6D.p=5,q=-69.用科学记数法表示为A.B.C.D.10.若,则下列不等式中不成立的是()A.B.C.D.11.下列等式从左到右的变形,属于因式分解的是A.8a2b=2a·4abB.-ab3-2ab2-ab=-ab(b2+2b)C.4x2+8x-4=4xD.4my-2=2(2my-1)12.如图,在平面直角坐标系上有点,点第一次跳动至点,第二次点跳动至点,第三次点跳动至点,第四次点跳动至点,……依此规律跳动下去,则点与点之间的距离是()A.2021B.2020C.2019D.2018二、填空题(每题4分,满分20分,将答案填在答题纸上)13.已知直线a∥b,点M到直线a的距离是5cm,到直线b的距离是3cm,那么直线a和直线b之间的距离为______cm.14.计算:____________.15.三河中学在全县中学生运动会上,共派出了30名运动员,占所有运动员总数的5%,则这次运动会全县共有_____名运动员.16.因式分解______17.某种细菌的存活时间只有0.000012秒,若用科学记数法表示此数据应为________秒三、解答题(本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)18.(5分)(1)求时,式子的值;(2)解方程组19.(5分)在一个不透明的口袋里装有仅颜色不同的黑、白两种颜色的球20只,某学习小组做摸球实验.将球搅匀后从中随机摸出一个球,记下颜色,再把它放回袋中,不断重复,下表是活动进行中记下的一组数据摸球的次数n1001502005008001000摸到白球的次数m5896116295484601摸到白球的频率0.580.640.580.590.6050.601(1)请你估计,当n很大时,摸到白球的频率将会接近(精确到0.1).(2)假如你去摸一次,你摸到白球的概率是,摸到黑球的概率是.(3)试估算口袋中黑、白两种颜色的球有多少只.20.(8分)解不等式组,并把其解集在数轴上表示出来.21.(10分)如图,点、在上,已知,,说明的理由.22.(10分)如图,已知∠A=∠F,∠C=∠D,请问BD与CE平行吗?并说明理由.23.(12分)杨辉三角形,又称贾宪三角形,帕斯卡三角形,是二项式系数在三角形中的一种几何排列,在我国南宋数学家杨所著的《详解九章算术》(1261年)一书中用如图的三角形解释二项和的乘方规律(a+b)1=a+b(a+b)2=a2+2ab+b2(a+b)3=(a+b)(a2+2ab+b2)=a3+3a2b+3ab2+b3(a+b)4=(a+b)(a3+3a2b+3ab2+b3)=a4+4a3b+6a2b2+4ab3+b4“杨辉三角”里面蕴藏了许多的规律(1)找出其中各项字母之间的规律以及各项系数之间的规律各一条;(2)直接写出(a+b)6展开后的多项式;(3)运用:若今天是星期四,经过84天后是星期,经过8100天后是星期.参考答案一、选择题:本大题共12个小题,每小题3分,共36分.在每小题...