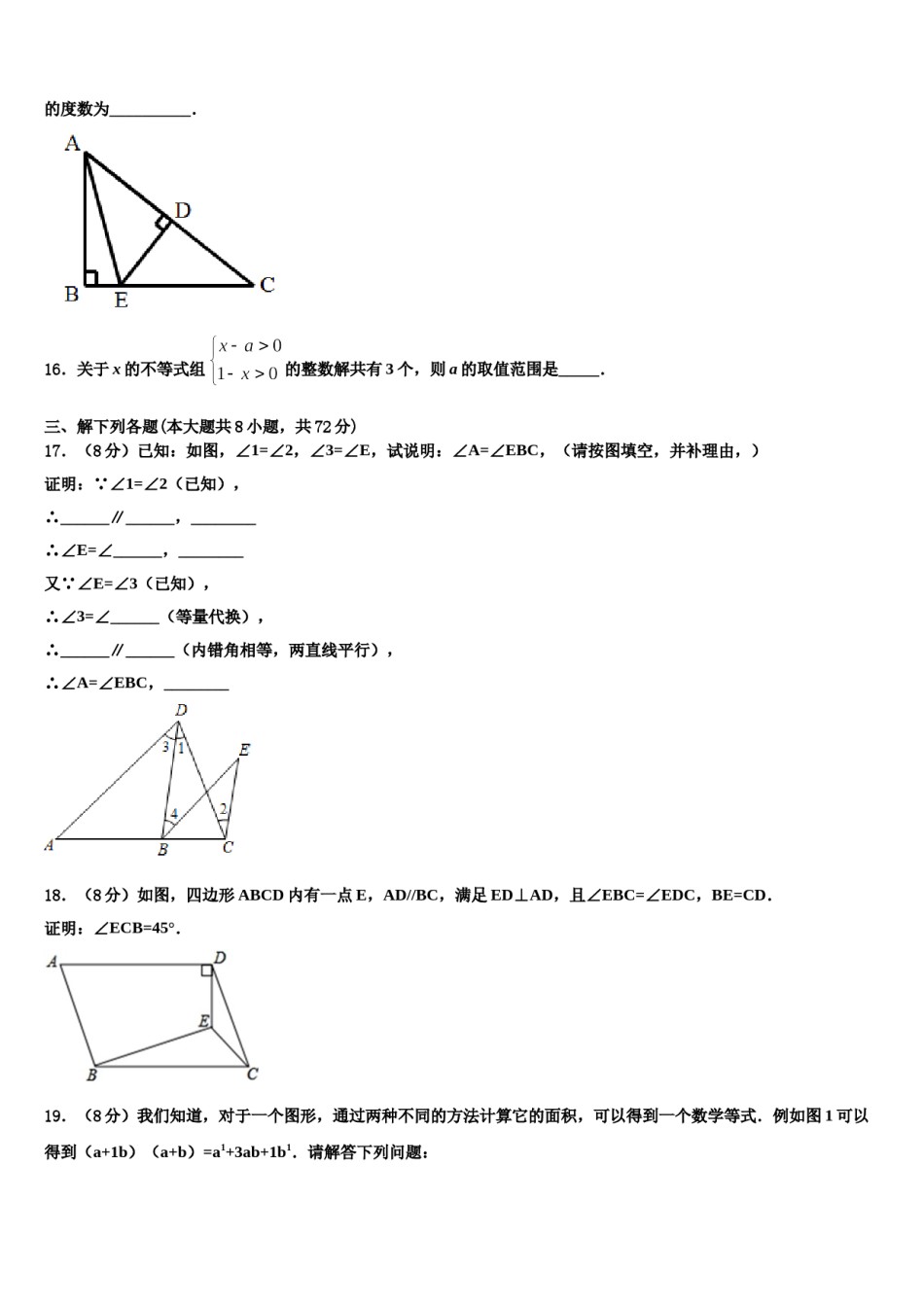
2023-2024学年七下数学期末模拟试卷注意事项铅笔作答;第二部分必须用黑1.考生要认真填写考场号和座位序号。2.试题所有答案必须填涂或书写在答题卡上,在试卷上作答无效。第一部分必须用2B色字迹的签字笔作答。3.考试结束后,考生须将试卷和答题卡放在桌面上,待监考员收回。一、选择题(每小题3分,共30分)1.在,,,3.14,0.121221…(每两个1之间依次递增2)中无理数有()A.2个B.3个C.4个D.5个2.如图,将正方形纸片ABCD折叠,使点D落在边AB上的D'处,点C落在C'处,若∠AD'M=50°,则∠MNC'的度数为()A.100°B.110°C.120°D.130°3.下列说法不一定成立的是()A.若a>b,则a+c>b+cB.若2a>-2b,则a>-bC.若a>b,则ac2>bc2D.若a<b,则a-2<b+14.如图所示是最近微信朋友圈常被用来“醒醒盹,动动脑”的图片,请你一定认真观察,动动脑子想一想,图中的?表示什么数()A.25B.15C.12D.145.如图,在数轴上,点A表示1,现将点A沿数轴做如下移动:第一次将点A向左移动3个单位长度到达点A1,第二次将点A向右移动6个单位长度到达点A2,第三次将点A2向左移动9个单位长度到达点A3,按照这种移动规律移动下去,第n次移动到点An,如果点An与原点的距离不小于20,那么n的最小值是()A.12B.13C.14D.156.下列实数是负数的是()A.B.36C.0D.﹣107.把点A(3,﹣4)先向上平移4个单位,再向左平移3个单位得到点B,则点B坐标为()A.(0,﹣8)B.(6,﹣8)C.(﹣6,0)D.(0,0)8.下列说法中:①三角形中至少有2个角是锐角;②各边都相等的多边形是正多边形;③钝角三角形的三条高交于一点;④两个等边三角形全等;⑤三角形两个内角的平分线的交点到三角形三边的距离相等,正确的个数是()A.1B.2C.3D.49.如图,小明从点O出发,先向西走40米,再向南走30米到达点M,如果点M的位置用(-40,-30)表示,那么(10,20)表示的位置是()A.点AB.点BC.点CD.点D10.下列命题中,是真命题的是()A.三角形的一条角平分线将三角形的面积平分B.同位角相等C.如果a2=b2,那么a=bD.是完全平方式二、填空题(本大题共有6小题,每小题3分,共18分)11.已知方程组,则x+y=______.12.掷一枚硬币30次,有12次正面朝上,则正面朝上的频率为.13.指出命题“对顶角相等”的题设和结论,题设_____,结论_____.14.已知OA⊥OC于O,∠AOB∶∠AOC=2∶3,则∠BOC的度数为____________度.15.如图,在中,,的垂直平分线分别交、于点、.已知,则的度数为__________.16.关于x的不等式组的整数解共有3个,则a的取值范围是_____.三、解下列各题(本大题共8小题,共72分)17.(8分)已知:如图,∠1=∠2,∠3=∠E,试说明:∠A=∠EBC,(请按图填空,并补理由,)证明: ∠1=∠2(已知),∴______∥______,________∴∠E=∠______,________又 ∠E=∠3(已知),∴∠3=∠______(等量代换),∴______∥______(内错角相等,两直线平行),∴∠A=∠EBC,________18.(8分)如图,四边形ABCD内有一点E,AD//BC,满足ED⊥AD,且∠EBC=∠EDC,BE=CD.证明:∠ECB=45°.19.(8分)我们知道,对于一个图形,通过两种不同的方法计算它的面积,可以得到一个数学等式.例如图1可以得到(a+1b)(a+b)=a1+3ab+1b1.请解答下列问题:(1)写出图1中所表示的数学等式;(1)利用(1)中所得到的结论,解决下面的问题:已知a+b+c=11,ab+bc+ac=47,求a1+b1+c1的值;(3)小明同学又用x张边长为a的正方形,y张边长为b的正方形,z张边长为a、b的长方形纸片拼出了一个面积为(15a+8b)(17a+44b)长方形,求x+y+z的值.20.(8分)化简求值:当时,求的值.21.(8分)蕲春新长途客运站准备在七一前建成营运,后期工程若请甲乙两个工程队同时施工,8天可以完工,需付两工程队施工费用7040元;若先请甲工程队单独施工6天,再请乙工程队单独施工12天可以完工,需付两工程队施工费用6960元。(1)甲、乙两工程队施工一天,应各付施工费用多少元?(2)若想付费用较少,选择哪个工程队?若想尽早完工,选择哪个工程队?22.(10分)(1)选择合适的方法解下列方程组(2)解不等式组,并把解...