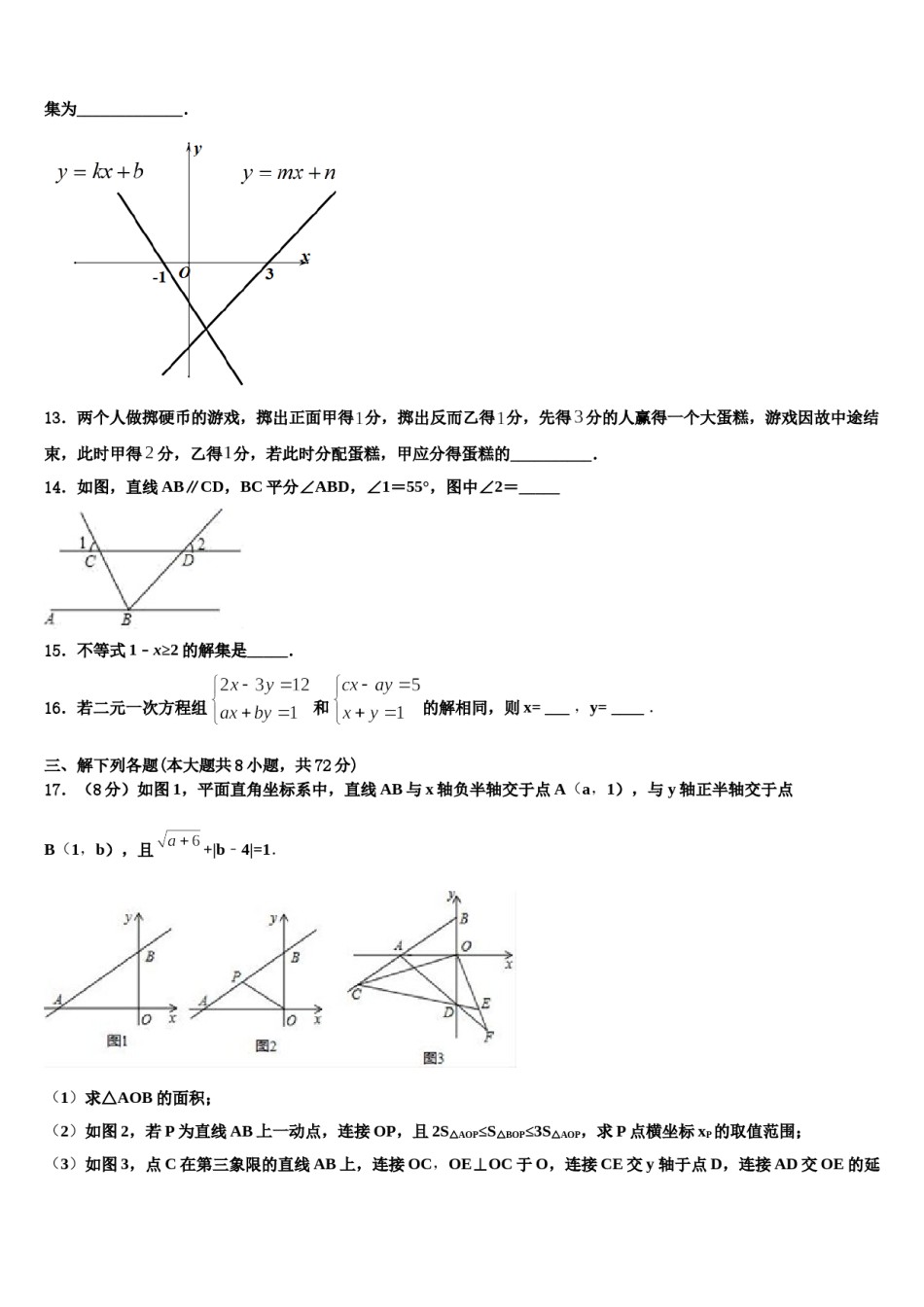
2023-2024学年七下数学期末模拟试卷考生须知:1.全卷分选择题和非选择题两部分,全部在答题纸上作答。选择题必须用2B铅笔填涂;非选择题的答案必须用黑色字迹的钢笔或答字笔写在“答题纸”相应位置上。2.请用黑色字迹的钢笔或答字笔在“答题纸”上先填写姓名和准考证号。3.保持卡面清洁,不要折叠,不要弄破、弄皱,在草稿纸、试题卷上答题无效。一、选择题(每小题3分,共30分)1.已知实数a,b,若a>b,则下列结论错误的是()A.a-5>b-5B.3+a>b+3C.>D.-3a>-3b2.下列各式计算结果正确的是()B.a4•a2=a8A.(a2)5=a7D.(a2b)3=a6b3C.(a﹣b)2=a2﹣b23.如图所示,在中,,,直线过点,并交边于点,点到直线的距离,点到直线的距离,则线段的长是()A.2B.3C.5D.74.如图,在△ABC中,∠B、∠C的平分线BE,CD相交于点F,若∠BFC=116°,则∠A=()A.51°B.52°C.53°D.58°5.下列因式分解正确的是()A.+=(m+n)(m−n)B.−a=a(a−1)C.(x+2)(x−2)=−4D.+2x−1=(x−1)26.某中学开展“眼光体育一小时”活动,根据学校实际情况,如图决定开设“A:踢毽子,B:篮球,C:跳绳,D:乒乓球”四项运动项目(每位同学必须选择一项),为了解学生最喜欢哪一项运动项目,随机抽取了一部分学生进行调查,丙将调查结果绘制成如图的统计图,则参加调查的学生中最喜欢跳绳运动项目的学生数为()A.240B.120C.80D.407.观察下面图案,在(A)(B)(C)(D)四幅图案中,能通过图案(1)平移得到的是()A.B.C.D.8.如果分式的值为零,则的值是()A.2B.-2C.D.0,点的坐标,将线段9.在平面直角坐标系中,点的坐标平移,使得到达点,点到C.的解达点,则点的坐标是()A.B.D.10.若,,则、的大小关系为()A.>B.<C.=D.无法确定二、填空题(本大题共有6小题,每小题3分,共18分)11.若a﹣b=1,ab=﹣2,则(a﹣2)(b+2)=______.12.如图,直线与直线分别与x轴交于点(-1,0)、(3,0),则不等式集为_____________.13.两个人做掷硬币的游戏,掷出正面甲得分,掷出反而乙得分,先得分的人赢得一个大蛋糕,游戏因故中途结束,此时甲得分,乙得分,若此时分配蛋糕,甲应分得蛋糕的__________.14.如图,直线AB∥CD,BC平分∠ABD,∠1=55°,图中∠2=_____15.不等式1﹣x≥2的解集是_____.16.若二元一次方程组和的解相同,则x=___,y=____.三、解下列各题(本大题共8小题,共72分)17.(8分)如图1,平面直角坐标系中,直线AB与x轴负半轴交于点A(a,1),与y轴正半轴交于点B(1,b),且+b﹣4=1.(1)求△AOB的面积;(2)如图2,若P为直线AB上一动点,连接OP,且2S△AOP≤S△BOP≤3S△AOP,求P点横坐标xP的取值范围;(3)如图3,点C在第三象限的直线AB上,连接OC,OE⊥OC于O,连接CE交y轴于点D,连接AD交OE的延长线于F,则∠OAD、∠ADC、∠CEF、∠AOC之间是否有某种确定的数量关系?试证明你的结论.18.(8分)已知:如图,E是AC上一点,AB=CE,AB∥CD,∠ACB=∠D.求证:BC=ED.19.(8分)已知小正方形的边长为厘米,大正方形的边长为厘米,起始状态如图所示,大正方形固定不动,把小正方形以厘米/秒的速度向右沿直线平移,设平移的时间为秒,两个正方形重叠部分的面积为平方厘米。(1)当时,求的值;(2)当时,求小正方形平移的时间.(3)当时,求小正方形一条对角线扫过的面积。20.(8分)(1)如图,△ABC,∠ABC、∠ACB的三等分线交于点E、D,若∠1=130°,∠2=110°,求∠A的度数.(2)如图,△ABC,∠ABC的三等分线分别与∠ACB的平分线交于点D,E若∠1=110°,∠2=130°,求∠A的度数.21.(8分)以下是推导“三角形内角和定理”的学习过程,请补全证明过程及推理依据.己知:如图,.求证:.证明:过点作∥,(请在图上画出该辅助线并标注,两个字母)∴,①.(②) 点,,在同一条直线上,∴③,(平角的定义)∴.即三角形的内角和为180°22.(10分)阅读并填空:如图,是等腰三角形,,是边延长线上的一点,在边上且联接交于,如果,那么,为什么?解:过点作交于所以(两直线平行,同位角相等)(________)在与中所以,(...