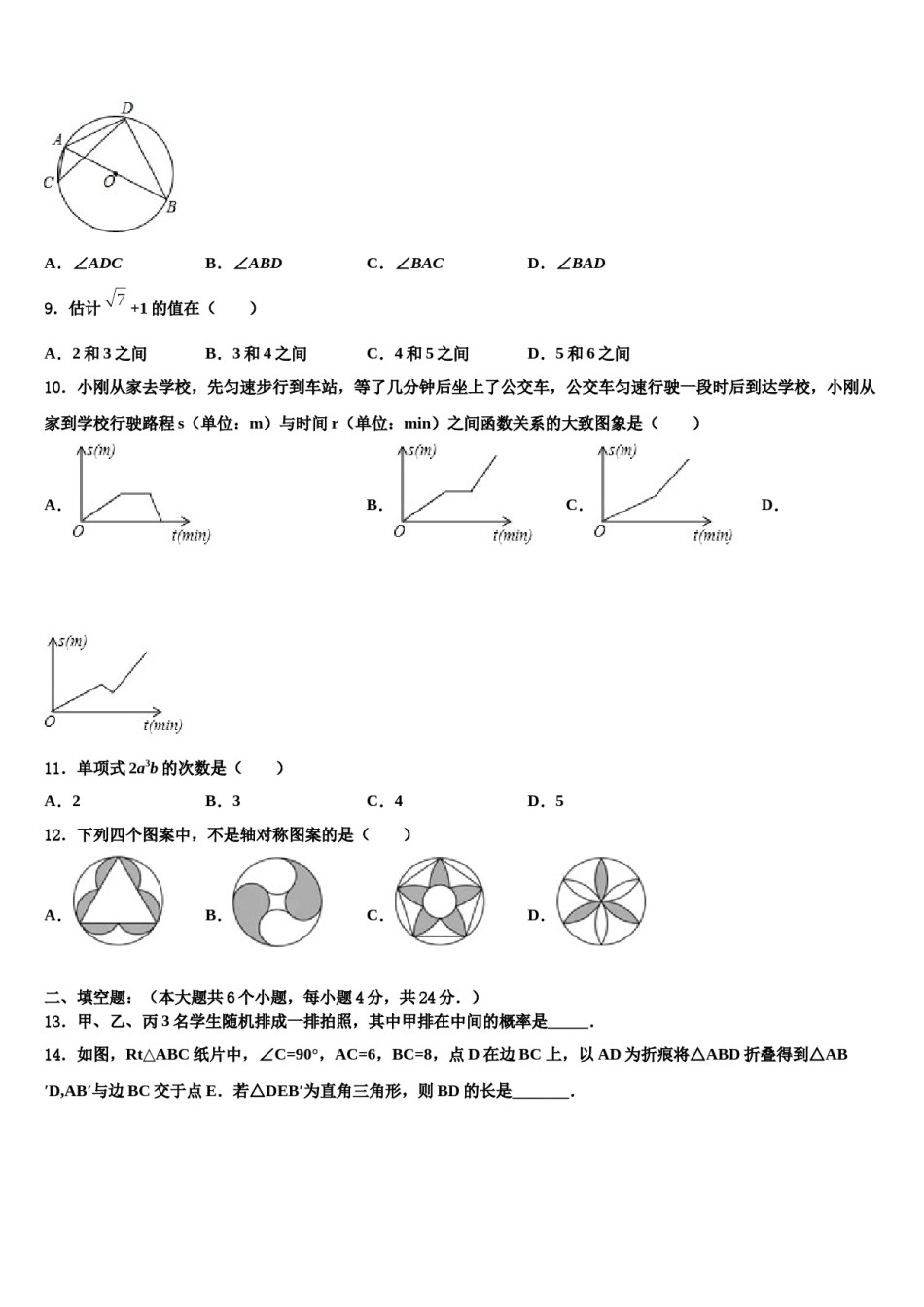
2024届河北省张家口市桥西区重点达标名校中考数学考前最后一卷请考生注意:1.请用2B铅笔将选择题答案涂填在答题纸相应位置上,请用0.5毫米及以上黑色字迹的钢笔或签字笔将主观题的答案写在答题纸相应的答题区内。写在试题卷、草稿纸上均无效。2.答题前,认真阅读答题纸上的《注意事项》,按规定答题。一、选择题(本大题共12个小题,每小题4分,共48分.在每小题给出的四个选项中,只有一项是符合题目要求的.)1.x=1是关于x的方程2x﹣a=0的解,则a的值是()A.﹣2B.2C.﹣1D.12.两个有理数的和为零,则这两个数一定是()A.都是零B.至少有一个是零C.一个是正数,一个是负数D.互为相反数3.把抛物线y=﹣2x2向上平移1个单位,得到的抛物线是()A.y=﹣2x2+1B.y=﹣2x2﹣1C.y=﹣2(x+1)2D.y=﹣2(x﹣1)24.下列计算正确的是()A.a2•a3=a6B.(a2)3=a6C.a2+a2=a3D.a6÷a2=a35.如图所示的四个图案是四国冬季奥林匹克运动会会徽图案上的一部分图形,其中为轴对称图形的是()A.B.C.D.6.若关于的一元二次方程有两个不相等的实数根,则的取值范围()A.B.C.且D.7.下列运算正确的是()A.=2B.4﹣=1C.=9D.=28.如图,AB是⊙O的直径,C,D是⊙O上位于AB异侧的两点.下列四个角中,一定与∠ACD互余的角是()A.∠ADCB.∠ABDC.∠BACD.∠BAD9.估计+1的值在()A.2和3之间B.3和4之间C.4和5之间D.5和6之间10.小刚从家去学校,先匀速步行到车站,等了几分钟后坐上了公交车,公交车匀速行驶一段时后到达学校,小刚从家到学校行驶路程s(单位:m)与时间r(单位:min)之间函数关系的大致图象是()A.B.C.D.11.单项式2a3b的次数是()A.2B.3C.4D.512.下列四个图案中,不是轴对称图案的是()A.B.C.D.二、填空题:(本大题共6个小题,每小题4分,共24分.)13.甲、乙、丙3名学生随机排成一排拍照,其中甲排在中间的概率是_____.14.如图,Rt△ABC纸片中,∠C=90°,AC=6,BC=8,点D在边BC上,以AD为折痕将△ABD折叠得到△AB′D,AB′与边BC交于点E.若△DEB′为直角三角形,则BD的长是_______.15.在Rt△ABC纸片上剪出7个如图所示的正方形,点E,F落在AB边上,每个正方形的边长为1,则Rt△ABC的面积为_____.16.的相反数是_____.17.分解因式:x2y﹣xy2=_____.18.如图,已知正六边形ABCDEF的外接圆半径为2cm,则正六边形的边心距是__________cm.三、解答题:(本大题共9个小题,共78分,解答应写出文字说明、证明过程或演算步骤.19.(6分)在△ABC中,已知AB=AC,∠BAC=90°,E为边AC上一点,连接BE.(1)如图1,若∠ABE=15°,O为BE中点,连接AO,且AO=1,求BC的长;(2)如图2,D为AB上一点,且满足AE=AD,过点A作AF⊥BE交BC于点F,过点F作FG⊥CD交BE的延长线于点G,交AC于点M,求证:BG=AF+FG.20.(6分)如图,在Rt△ABC中,,过点C的直线MN∥AB,D为AB边上一点,过点D作DE⊥BC,交直线MN于E,垂足为F,连接CD、BE.求证:CE=AD;当D在AB中点时,四边形BECD是什么特殊四边形?说明理由;若D为AB中点,则当=______时,四边形BECD是正方形.21.(6分)如图,半圆D的直径AB=4,线段OA=7,O为原点,点B在数轴的正半轴上运动,点B在数轴上所表示的数为m.当半圆D与数轴相切时,m=.半圆D与数轴有两个公共点,设另一个公共点是C.①直接写出m的取值范围是.②当BC=2时,求△AOB与半圆D的公共部分的面积.当△AOB的内心、外心与某一个顶点在同一条直线上时,求tan∠AOB的值.22.(8分)如图,AB是⊙O的直径,弦DE交AB于点F,⊙O的切线BC与AD的延长线交于点C,连接AE.(1)试判断∠AED与∠C的数量关系,并说明理由;(2)若AD=3,∠C=60°,点E是半圆AB的中点,则线段AE的长为.23.(8分)如图,矩形OABC中,点O为原点,点A的坐标为(0,8),点C的坐标为(6,0).抛物线经过A、C两点,与AB边交于点D.(1)求抛物线的函数表达式;(2)点P为线段BC上一个动点(不与点C重合),点Q为线段AC上一个动点,AQ=CP,连接PQ,设CP=m,△CPQ的面积为S.①求S关于m的函数表达式,并求出m为何值时,S取得最大值;②当S最大时,在抛...