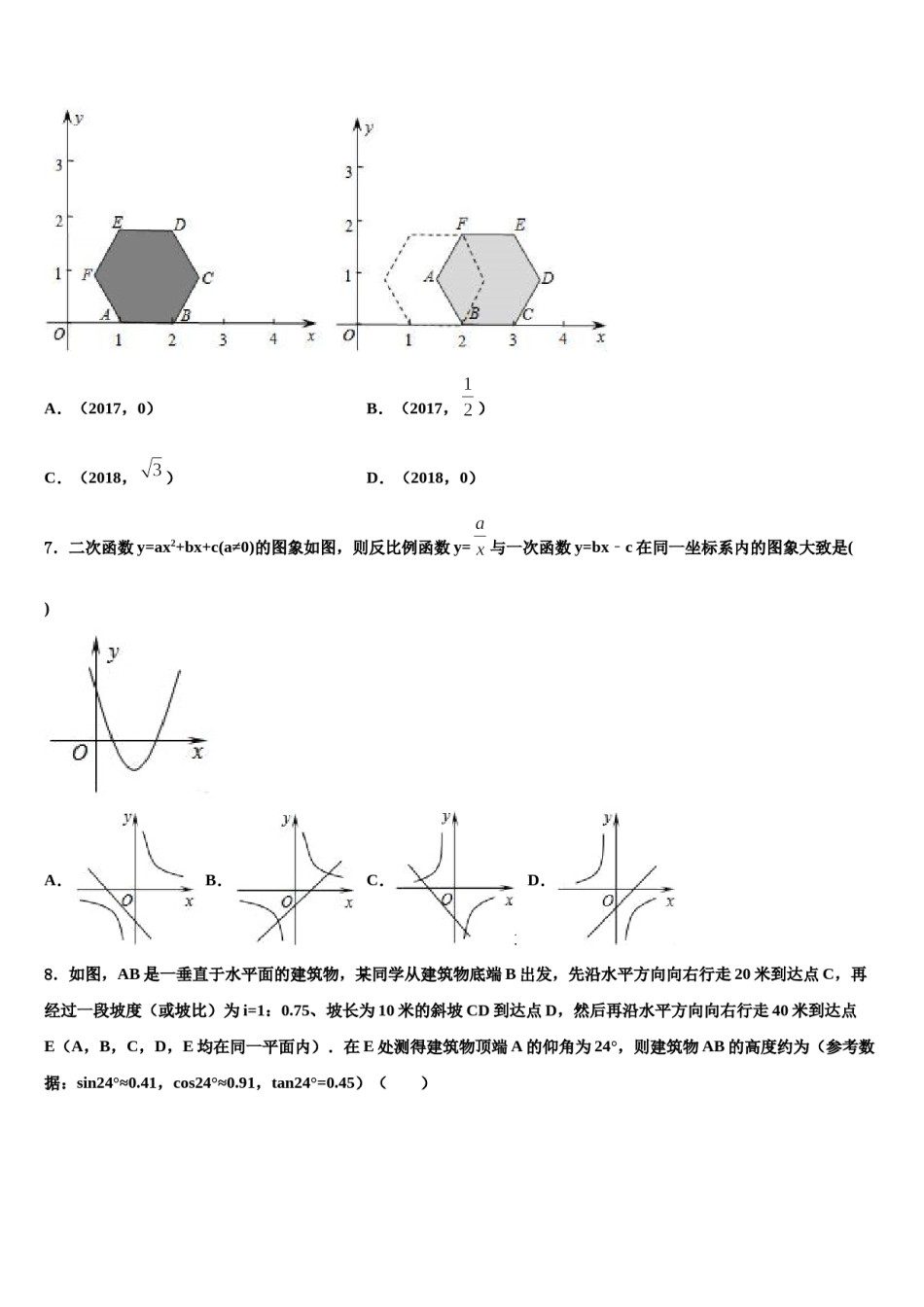
贵州省毕节市市级名校2024年中考四模数学试题请考生注意:1.请用2B铅笔将选择题答案涂填在答题纸相应位置上,请用0.5毫米及以上黑色字迹的钢笔或签字笔将主观题的答案写在答题纸相应的答题区内。写在试题卷、草稿纸上均无效。2.答题前,认真阅读答题纸上的《注意事项》,按规定答题。一、选择题(共10小题,每小题3分,共30分)1.如图,半径为1的圆O1与半径为3的圆O2相内切,如果半径为2的圆与圆O1和圆O2都相切,那么这样的圆的个数是()A.1B.2C.3D.42.抛物线y=mx2﹣8x﹣8和x轴有交点,则m的取值范围是()A.m>﹣2B.m≥﹣2C.m≥﹣2且m≠0D.m>﹣2且m≠03.有理数a、b在数轴上的位置如图所示,则下列结论中正确的是()A.a+b>0B.ab>0C.a﹣b<oD.a÷b>04.如果解关于x的分式方程时出现增根,那么m的值为A.-2B.2C.4D.-45.计算﹣1﹣(﹣4)的结果为()A.﹣3B.3C.﹣5D.56.如图,在平面直角坐标系xOy中,点A(1,0),B(2,0),正六边形ABCDEF沿x轴正方向无滑动滚动,每旋转60°为滚动1次,那么当正六边形ABCDEF滚动2017次时,点F的坐标是()A.(2017,0)B.(2017,)C.(2018,)D.(2018,0)7.二次函数y=ax2+bx+c(a≠0)的图象如图,则反比例函数y=与一次函数y=bx﹣c在同一坐标系内的图象大致是()A.B.C.D.8.如图,AB是一垂直于水平面的建筑物,某同学从建筑物底端B出发,先沿水平方向向右行走20米到达点C,再经过一段坡度(或坡比)为i=1:0.75、坡长为10米的斜坡CD到达点D,然后再沿水平方向向右行走40米到达点E(A,B,C,D,E均在同一平面内).在E处测得建筑物顶端A的仰角为24°,则建筑物AB的高度约为(参考数据:sin24°≈0.41,cos24°≈0.91,tan24°=0.45)()A.21.7米B.22.4米C.27.4米D.28.8米9.如图,点E是四边形ABCD的边BC延长线上的一点,则下列条件中不能判定AD∥BE的是()A.B.C.D.10.实数a,b在数轴上的对应点的位置如图所示,则正确的结论是()A.a>﹣2B.a<﹣3C.a>﹣bD.a<﹣b二、填空题(本大题共6个小题,每小题3分,共18分)11.已知二次函数f(x)=x2-3x+1,那么f(2)=_________.12.将绕点逆时针旋转到使、、在同一直线上,若,,,则图中阴影部分面积为________.13.股市规定:股票每天的涨、跌幅均不超过10%,即当涨了原价的10%后,便不能再涨,叫做涨停;当跌了原价的10%后,便不能再跌,叫做跌停.若一支股票某天跌停,之后两天时间又涨回到原价,若这两天此股票股价的平均增长率为x,则x满足的方程是_____.14.如图,在菱形ABCD中,于E,,,则菱形ABCD的面积是______.15.等腰中,是BC边上的高,且,则等腰底角的度数为__________.16.从某玉米种子中抽取6批,在同一条件下进行发芽试验,有关数据如下:种子粒数100400800100020005000发芽种子粒数8531865279316044005发芽频率0.8500.7950.8150.7930.8020.801根据以上数据可以估计,该玉米种子发芽的概率为___________(精确到0.1).的中点.三、解答题(共8题,共72分)17.(8分)已知:如图,在△ABC中,∠ACB=90°,以BC为直径的⊙O交AB于点D,E为求证:∠ACD=∠DEC;(2)延长DE、CB交于点P,若PB=BO,DE=2,求PE的长18.(8分)在平面直角坐标系xOy中,抛物线y=ax2+2ax+c(其中a、c为常数,且a<0)与x轴交于点A(﹣3,0),与y轴交于点B,此抛物线顶点C到x轴的距离为1.(1)求抛物线的表达式;(2)求∠CAB的正切值;(3)如果点P是x轴上的一点,且∠ABP=∠CAO,直接写出点P的坐标.19.(8分)先化简,再求值:(﹣m+1)÷,其中m的值从﹣1,0,2中选取.20.(8分)已知:如图1在Rt△ABC中,∠C=90°,AC=8cm,BC=6cm,点P由点B出发沿BA方向向点A匀速运动,速度为2cm/s;同时点Q由点A出发沿AC方向点C匀速运动,速度为lcm/s;连接PQ,设运动的时间为t秒(0<t<5),解答下列问题:(1)当为t何值时,PQ∥BC;(2)设△AQP的面积为y(cm2),求y关于t的函数关系式,并求出y的最大值;(3)如图2,连接PC,并把△PQC沿QC翻折,得到四边形PQPC,是否存在某时刻t,使四边形PQP'C为菱形?若存在,求出此时t的值;若不存在,请说...