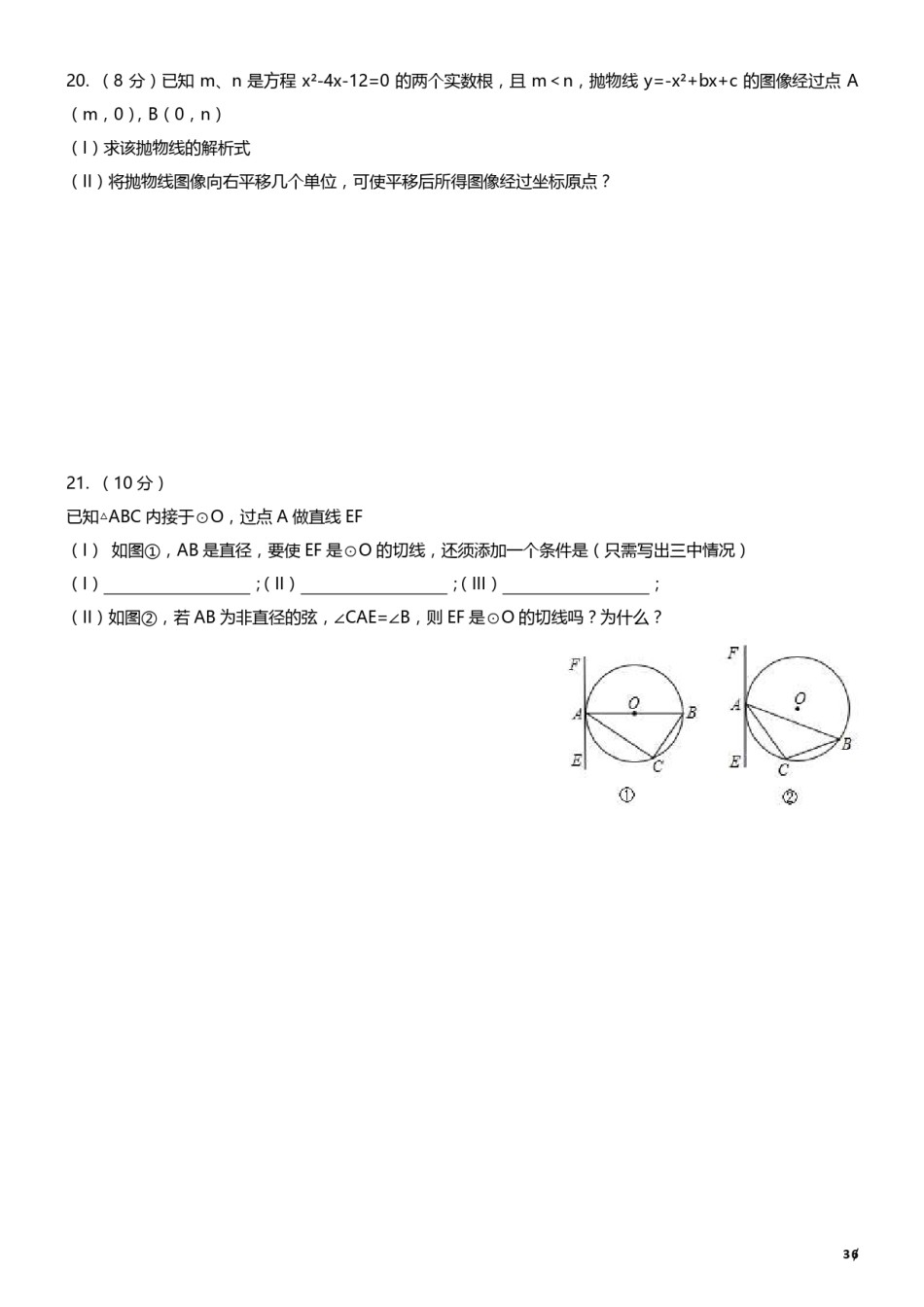
2017-2018年度南开区初三期中考试数学试卷一、选择题(3×12=36)1.关于x的一元二次方程x²+3x+m=0有两个不相等的实数根,则m的可以取的数值为A.9B.7C.9D.7442.下面四个手机应用图标中,属于中心对称图形的是A.B.C.D.3.对于二次函数y=-(x-1)²+2的图像与性质,下列说法正确的是A.对称轴是x=1,最大值是2B.对称轴是x=1,最小值是2C.对称轴是x=-1,最大值是2D.对称轴是x=1,最小值是24.不论x为何值,函数y=ax²+bx+c(a≠0)的值恒大于0的条件是A.a>0,△>0B.a>0,△<0C.a<0,△<0D.a<0,△>05.如图,A,B,C,D是⊙O上的四个点,B是弧AC的中点,M是半径OD上任意一点,若BDC=40°,则∠AMB的度数不可能是A.45°B.60°C.75°D.85°6.下列命题中,正确的是A.圆心角相等,所对的弦的弦心距相等B.三点确定一个圆C.平分弦的直径垂直于弦,并且平分弦所对的弧D.弦的垂直平分线必经过圆心7.如图,边长为4的正六边形ABCDEF的中心与坐标原点O重合,AF∥x轴,将正六边形ABCDEF绕原点O顺时针旋转n次,每次旋转60°,当n=2017时,顶点A的坐标为A.(4,0)B.(-4,0)C.(2,23)D.(-2,23)8.如图,正五边形ABCDE内接于⊙O,点M为BC中点,点N为DE中点,则∠MON的大小为A.108°B.144°C.150°D.166°9.已知⊙O的半径为R,其内接正六边形,正四边形,正三角形的边长分别为a,b,c,则a:b:c的值为A.1:2:3B.3:2:1C1:2:3D.3:2:110.如图,在边长为1的正方形ABCD中,将射线AC绕点A按顺时针方向旋转α度(0<α≤360)得到射线AE,点M是点D关于射线AE的对称点,则线段CM的最小值为A.2-1B.0.5C.1D.2+116/11.在同一平面坐标系中,函数y=mx+m和y=-mx²+2x+2(m是常数,且m≠0)的图像可能是A.B.C.D.12.如图,直线y=kx+c与抛物线y=ax²+bx+c的图像都经过y轴上D点,抛物线与x轴交于A、B两点,其对称轴为直线x=1,且OA=OD,直线y=kx+c与x轴交于点C(点C在点B的右侧),则下列命题中正确命题的个数是:①abc>0;②3a+b>0;③-1<k<0;④k>a+b;⑤ac+k>0A.1B.2C.3D.4二、填空题(3×6=18)13.点P(2,-1)关于原点的对称点坐标为(-2,m),则m=14.二次函数y=x²+3x-2,当x满足时,y随x的增大而增大15.将二次函数y=x²+1的图像向左平移2个单位,再向下平移3个单位,所得二次函数解析式为16.如图,在Rt△ABC中,∠ACB=90°,将△ABC绕顶点C逆时针旋转得到△A’B’C,M是BC的中点,P是A’B’的中点,连接PM,若BC=2,∠BAC=30°,则线段PM的最大值是17.受益于国家支持新能源汽车发展等多重利好因素,我市某汽车零部件生产企业的利润逐年提高,据统计,2014年利润为2亿元,2016年利润为2.88亿元,则该企业从2014年到2016年利润的平均增长率为;若2017年保持前两年利润的年平均增长率不变,该企业2017年的利润(填“能”或“不能”)超过3.4亿元18.已知,如图,AB是⊙O的直径,点P在BA的延长线上,弦CD交AB于E,连接OD、PC、BC,∠AOD=2∠ABC,∠P=∠D,过E做弦GF⊥BC交圆于G、F两点,连接CF,BG,则下列结论:①CD⊥AB;②1(只需填序号)PC是⊙O的切线;③OD∥GF;④弦CF的弦心距等于BG,则其中正确的是2三、解答题(66分)719.(8分)按要求解一元二次方程(II)x²-x-=0(配方法)(I)(3x-1)²=(x+1)²(适当方法)426/20.(8分)已知m、n是方程x²-4x-12=0的两个实数根,且m<n,抛物线y=-x²+bx+c的图像经过点A(m,0),B(0,n)(I)求该抛物线的解析式(II)将抛物线图像向右平移几个单位,可使平移后所得图像经过坐标原点?21.(10分)已知△ABC内接于⊙O,过点A做直线EF(I)如图①,AB是直径,要使EF是⊙O的切线,还须添加一个条件是(只需写出三中情况)(I);(II);(III);(II)如图②,若AB为非直径的弦,∠CAE=∠B,则EF是⊙O的切线吗?为什么?36/22.(10分)如图,在△ABC中,点O在边AC上,⊙O与△ABC的边BC、AB分别相切于C、D两点,与边AC交于E点,弦CF与AB平行,与DO的延长线交于点M(I)求证:点M是CF的中点(II)若E是弧DF的中点,BC=2,求⊙O的半径23.某校拟在操场围建一生物种植活动区,活动区的一面靠现有墙(墙足够长),已知计划中的建筑材料课建围墙的总...