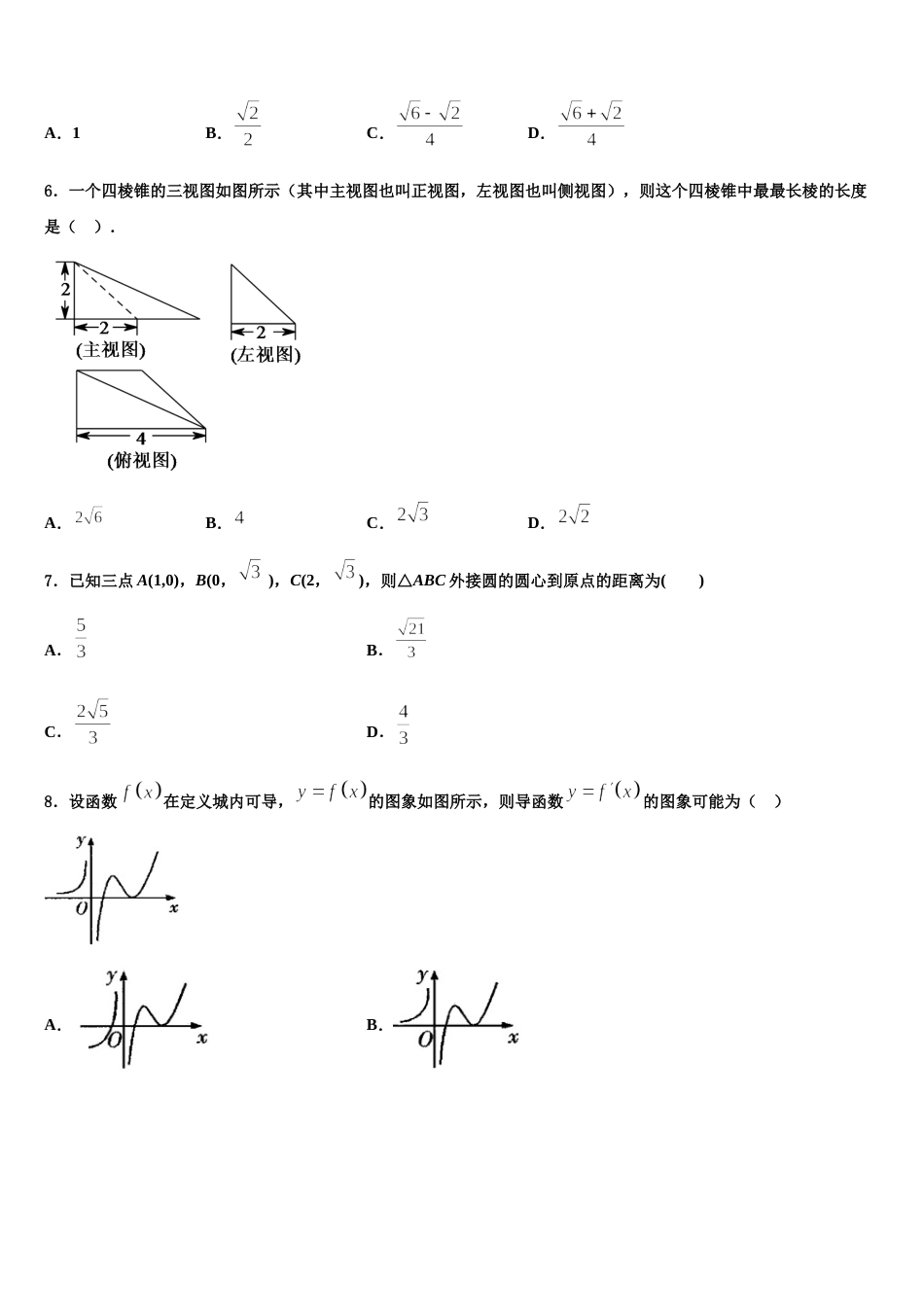
2023-2024 学年吉林省“五地六校”合作体高考数学全真模拟密押卷考生请注意:1.答题前请将考场、试室号、座位号、考生号、姓名写在试卷密封线内,不得在试卷上作任何标记。2.第一部分选择题每小题选出答案后,需将答案写在试卷指定的括号内,第二部分非选择题答案写在试卷题目指定的位置上。3.考生必须保证答题卡的整洁。考试结束后,请将本试卷和答题卡一并交回。一、选择题:本题共 12 小题,每小题 5 分,共 60 分。在每小题给出的四个选项中,只有一项是符合题目要求的。1.已知,则( )A.B.C.D.2.设正项等差数列的前项和为,且满足,则的最小值为A.8B.16C.24D.363.已知函数在上都存在导函数,对于任意的实数都有,当时,,若,则实数的取值范围是( )A.B.C.D.4.已知函数且,则实数的取值范围是( )A.B.C.D.5.在中,,,分别为角,,的对边,若的面为,且,则( )A.1B.C.D.6.一个四棱锥的三视图如图所示(其中主视图也叫正视图,左视图也叫侧视图),则这个四棱锥中最最长棱的长度是( ).A.B.C.D.7.已知三点 A(1,0),B(0, ),C(2,),则△ABC 外接圆的圆心到原点的距离为( )A.B.C.D.8.设函数在定义城内可导,的图象如图所示,则导函数的图象可能为( )A.B.C.D.9.已知抛物线的焦点与双曲线的一个焦点重合,且抛物线的准线被双曲线截得的线段长为,那么该双曲线的离心率为( )A.B.C.D.10.公元前世纪,古希腊哲学家芝诺发表了著名的阿基里斯悖论:他提出让乌龟在跑步英雄阿基里斯前面米处开始与阿基里斯赛跑,并且假定阿基里斯的速度是乌龟的倍.当比赛开始后,若阿基里斯跑了米,此时乌龟便领先他米,当阿基里斯跑完下一个米时,乌龟先他米,当阿基里斯跑完下-个米时,乌龟先他 米....所以,阿基里斯永远追不上乌龟.按照这样的规律,若阿基里斯和乌龟的距离恰好为米时,乌龟爬行的总距离为( )A.米B.米C.米D.米11.某高中高三(1)班为了冲刺高考,营造良好的学习氛围,向班内同学征集书法作品贴在班内墙壁上,小王,小董,小李各写了一幅书法作品,分别是:“入班即静”,“天道酬勤”,“细节决定成败”,为了弄清“天道酬勤”这一作品是谁写的,班主任对三人进行了问话,得到回复如下:小王说:“入班即静”是我写的;小董说:“天道酬勤”不是小王写的,就是我写的;小李说:“细节决定成败”不是我写的.若三人的说法有且仅有一人是正确的,则“入班即静”的书写者是( )A.小王或小李B.小王C.小董D.小李12.,则与位置关系是 ( )A.平行B.异面C.相交D.平行或异面或相交二、填空题:本题共 4 小题,每小题 5 分,共 20 分。13.若,则__________.14.记为数列的前项和.若,则______.15.已知是第二象限角,且,,则____.16.已知等差数列满足,,则的值为________.三、解答题:共 70 分。解答应写出文字说明、证明过程或演算步骤。17.(12 分)已知等差数列的公差,且,,成等比数列.(1)求数列的通项公式;(2)设,求数列的前项和.18.(12 分)已知△ABC 三内角 A、B、C 所对边的长分别为 a,b,c,且 3sin2A+3sin2B=4sinAsinB+3sin2C.(1)求 cosC 的值;(2)若 a=3,c,求△ABC 的面积.19.(12 分)已知函数的导函数的两个零点为和.(1)求的单调区间;(2)若的极小值为,求在区间上的最大值.20.(12 分)4 月 23 日是“世界读书日”,某中学开展了一系列的读书教育活动.学校为了解高三学生课外阅读情况,采用分层抽样的方法从高三某班甲、乙、丙、丁四个读书小组(每名学生只能参加一个读书小组)学生抽取 12 名学生参加问卷调查.各组人数统计如下:小组甲乙丙丁人数12969(1)从参加问卷调查的 12 名学生中随机抽取 2 人,求这 2 人来自同一个小组的概率;(2)从已抽取的甲、丙两个小组的学生中随机抽取 2 人,用表示抽得甲组学生的人数,求随机变量的分布列和数学期望.21.(12 分)某艺术品公司欲生产一款迎新春工艺礼品,该礼品是由玻璃球面和该球的内接圆锥组成,圆锥的侧面用于艺术装饰,如图 1.为了便于设计...