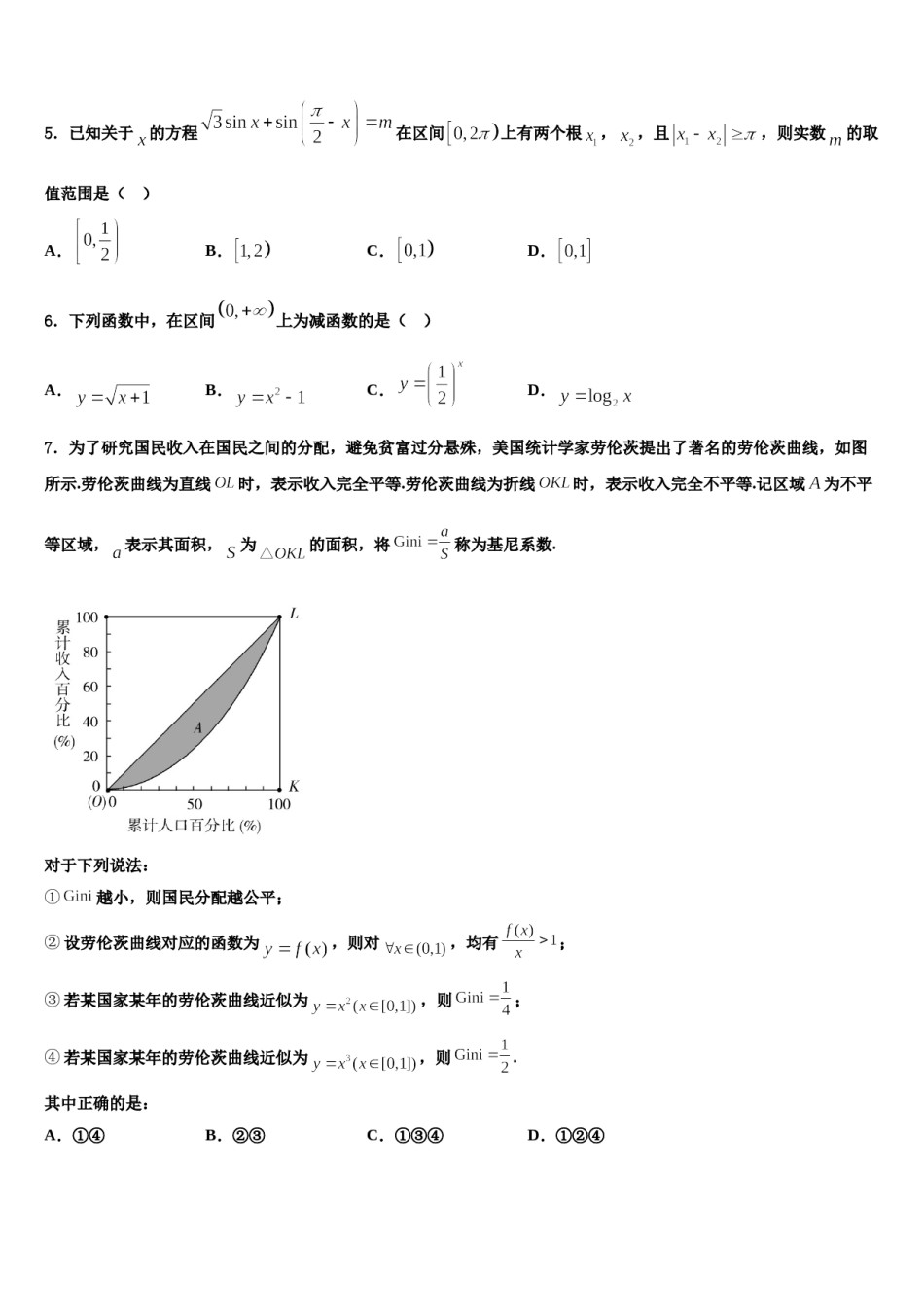
2023-2024学年四川省重庆市第八中学高考适应性考试数学试卷注意事项铅笔作答;第二部分必须用黑1.考生要认真填写考场号和座位序号。2.试题所有答案必须填涂或书写在答题卡上,在试卷上作答无效。第一部分必须用2B色字迹的签字笔作答。3.考试结束后,考生须将试卷和答题卡放在桌面上,待监考员收回。一、选择题:本题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的。1.已知,,则()A.B.C.3D.42.已知.给出下列判断:①若,且,则;②存在使得的图象向右平移个单位长度后得到的图象关于轴对称;③若在上恰有7个零点,则的取值范围为;④若在上单调递增,则的取值范围为.D.4其中,判断正确的个数为()A.1B.2C.33.复数,是虚数单位,则下列结论正确的是A.B.的共轭复数为C.的实部与虚部之和为1D.在复平面内的对应点位于第一象限4.已知双曲线的焦距是虚轴长的2倍,则双曲线的渐近线方程为()A.B.C.D.5.已知关于的方程在区间上有两个根,,且,则实数的取值范围是()A.B.C.D.6.下列函数中,在区间上为减函数的是()A.B.C.D.7.为了研究国民收入在国民之间的分配,避免贫富过分悬殊,美国统计学家劳伦茨提出了著名的劳伦茨曲线,如图所示.劳伦茨曲线为直线时,表示收入完全平等.劳伦茨曲线为折线时,表示收入完全不平等.记区域为不平等区域,表示其面积,为的面积,将称为基尼系数.对于下列说法:,则对,均有;①越小,则国民分配越公平;②设劳伦茨曲线对应的函数为③若某国家某年的劳伦茨曲线近似为,则;④若某国家某年的劳伦茨曲线近似为,则.C.①③④D.①②④其中正确的是:B.②③A.①④8.已知水平放置的△ABC是按“斜二测画法”得到如图所示的直观图,其中B′O′=C′O′=1,A′O′=,那么原△ABC的面积是()A.B.2C.D.9.在三角形中,,,求()A.B.C.D.10.下列函数中,既是奇函数,又是上的单调函数的是()A.B.C.D.11.已知集合M={x﹣1<x<2},N={xx(x+3)≤0},则M∩N=()A.[﹣3,2)B.(﹣3,2)C.(﹣1,0]D.(﹣1,0)12.集合,,则()A.B.C.D.二、填空题:本题共4小题,每小题5分,共20分。13.在平面直角坐标系xOy中,A,B为x轴正半轴上的两个动点,P(异于原点O)为y轴上的一个定点.若以AB为直径的圆与圆x2+(y-2)2=1相外切,且∠APB的大小恒为定值,则线段OP的长为_____.14.已知实数,满足约束条件,则的最小值为______.15.已知,则的值为______.16.设满足约束条件,则目标函数的最小值为_.三、解答题:共70分。解答应写出文字说明、证明过程或演算步骤。17.(12分)在直角坐标系中,已知直线的直角坐标方程为,曲线的参数方程为(为参数),以直角坐标系原点为极点,轴的正半轴为极轴建立极坐标系,曲线的极坐标方程为.(1)求曲线和直线的极坐标方程;(2)已知直线与曲线、相交于异于极点的点,若的极径分别为,求的值.18.(12分)已知函数.(1)讨论的单调性;,证明:,,使(2)若,设.19.(12分)已知函数,.(1)求曲线在点处的切线方程;(2)求函数的单调区间;(3)判断函数的零点个数.20.(12分)己知函数.(1)当时,求证:;(2)若函数,求证:函数存在极小值.21.(12分)已知四棱锥中,底面为等腰梯形,,,,丄底面.(1)证明:平面平面;(2)过的平面交于点,若平面把四棱锥分成体积相等的两部分,求二面角的余弦值.的左焦点和右焦点,椭圆的离心率为22.(10分)已知分别是椭圆是椭圆上两点,点满足.(1)求的方程;上,点为坐标原点,求的取值范围.(2)若点在圆参考答案一、选择题:本题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的。1、A【解析】根据复数相等的特征,求出和,再利用复数的模公式,即可得出结果.【详解】因为,所以,解得则.故选:A.【点睛】本题考查相等复数的特征和复数的模,属于基础题.2、B【解析】对函数化简可得,进而结合三角函数的最值、周期性、单调性、零点、对称性及平移变换,对四个命题逐个分析,可选出答案.,所以周期.【详解】因为对于①,因为,所以,即...