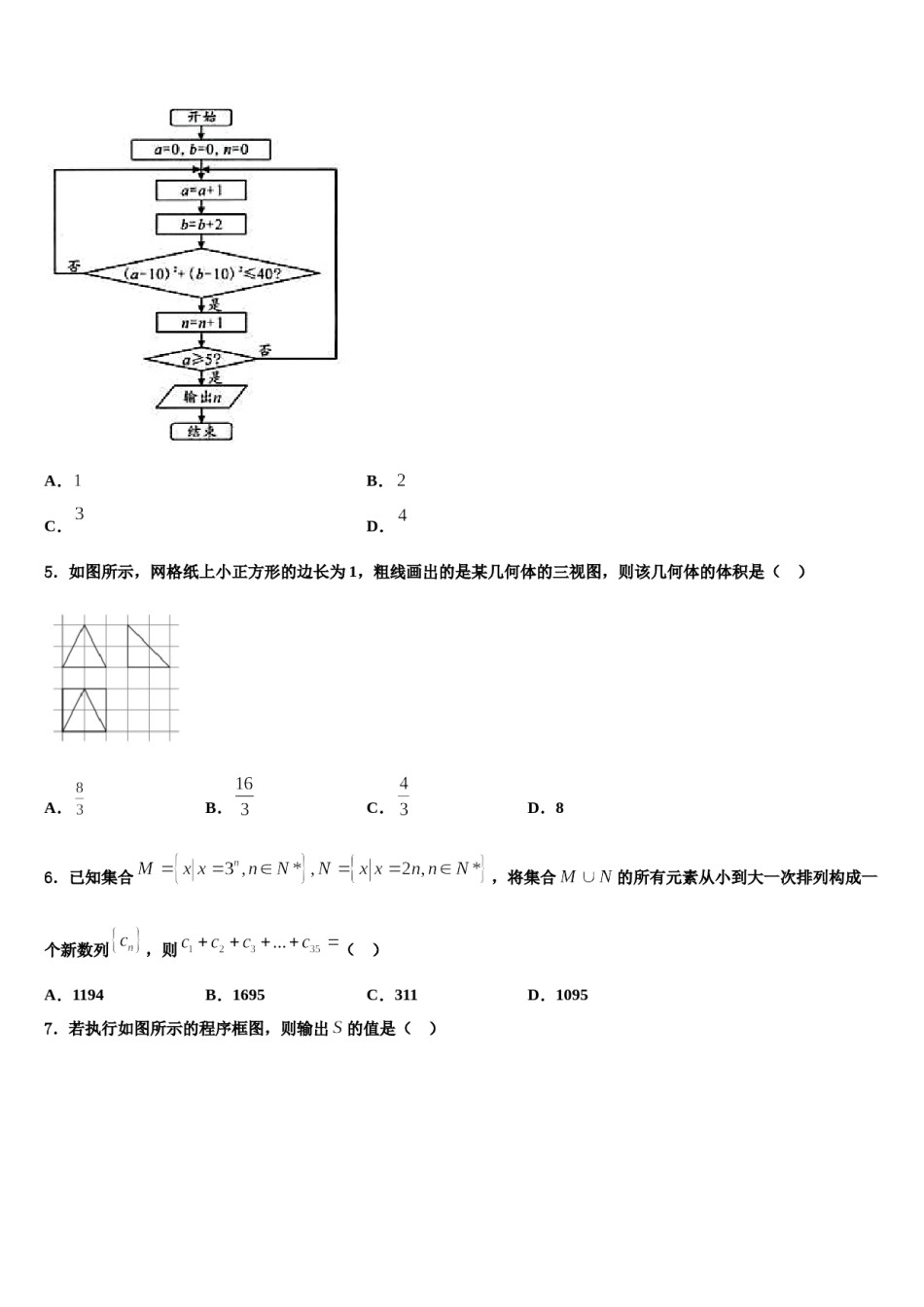
2023-2024学年山东省枣庄市高考压轴卷数学试卷考生请注意:1.答题前请将考场、试室号、座位号、考生号、姓名写在试卷密封线内,不得在试卷上作任何标记。2.第一部分选择题每小题选出答案后,需将答案写在试卷指定的括号内,第二部分非选择题答案写在试卷题目指定的位置上。3.考生必须保证答题卡的整洁。考试结束后,请将本试卷和答题卡一并交回。一、选择题:本题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的。1.已知集合,定义集合,则等于()A.B.C.D.2.波罗尼斯(古希腊数学家,的公元前262-190年)的著作《圆锥曲线论》是古代世界光辉的科学成果,它将圆锥曲线的性质网罗殆尽,几乎使后人没有插足的余地.他证明过这样一个命题:平面内与两定点距离的比为常数k(k>0,且k≠1)的点的轨迹是圆,后人将这个圆称为阿波罗尼斯圆.现有椭圆=1(a>b>0),A,B为椭圆的长轴端点,C,D为椭圆的短轴端点,动点M满足=2,△MAB面积的最大值为8,△MCD面积的最小值为D.1,则椭圆的离心率为()A.B.C.3.已知向量,,且与的夹角为,则()A.B.1C.或1D.或94.执行如图所示的程序框图,则输出的的值为()A.B.C.D.5.如图所示,网格纸上小正方形的边长为1,粗线画出的是某几何体的三视图,则该几何体的体积是()A.B.C.D.86.已知集合,将集合的所有元素从小到大一次排列构成一个新数列,则()A.1194B.1695C.311D.1095的值是()7.若执行如图所示的程序框图,则输出A.B.C.D.48.公差不为零的等差数列{an}中,a1+a2+a5=13,且a1、a2、a5成等比数列,则数列{an}的公差等于()A.1B.2C.3D.49.若,则()A.B.C.D.10.已知函数,关于的方程R)有四个相异的实数根,则的取值范围是()D.A.B.C.11.已知双曲线的一个焦点与抛物线的焦点重合,则双曲线的离心率为()A.B.C.3D.412.《周易》历来被人们视作儒家群经之首,它表现了古代中华民族对万事万物的深刻而又朴素的认识,是中华人文文化的基础,它反映出中国古代的二进制计数的思想方法.我们用近代术语解释为:把阳爻“-”当作数字“1”,把阴爻“--”当作数字“0”,则八卦所代表的数表示如下:卦名符号表示的二进制数表示的十进制数坤0000震0011坎0102兑0113依此类推,则六十四卦中的“屯”卦,符号“”表示的十进制数是()A.18B.17C.16D.15二、填空题:本题共4小题,每小题5分,共20分。13.已知函数,则函数的极大值为___________.14.如果函数(,且,)在区间上单调递减,那么的,且,若,则最大值为__________.15.的角所对的边分别为,的值为__________.16.已知点M是曲线y=2lnx+x2﹣3x上一动点,当曲线在M处的切线斜率取得最小值时,该切线的方程为_______.三、解答题:共70分。解答应写出文字说明、证明过程或演算步骤。17.(12分)设都是正数,且,.求证:.18.(12分)某公园有一块边长为3百米的正三角形空地,拟将它分割成面积相等的三个区域,用来种植三种花卉.方案是:先建造一条直道将分成面积之比为的两部分(点D,E分别在边,上);再取的中点M,建造直道(如图).设,,(单位:百米).(1)分别求,关于x的函数关系式;(为参数,).在以坐标原点(2)试确定点D的位置,使两条直道的长度之和最小,并求出最小值.19.(12分)在平面直角坐标系中,直线的参数方程为为极点、轴的非负半轴为极轴的极坐标系中,曲线的极坐标方程为.(1)若点在直线上,求直线的极坐标方程;(2)已知,若点在直线上,点在曲线上,且的最小值为,求的值.20.(12分)已知.(1)解关于x的不等式:;(2)若的最小值为M,且,求证:.,四边形EDCF为矩21.(12分)如图所示,直角梯形ABCD中,,,形,,平面平面ABCD.(1)求证:平面ABE;(2)求平面ABE与平面EFB所成锐二面角的余弦值.(3)在线段DF上是否存在点P,使得直线BP与平面ABE所成角的正弦值为,若存在,求出线段BP的长,若不存在,请说明理由.,分别是中点,且22.(10分)如图,在直三棱柱中,.求证:平面;求点到平面的距离.参考答案一、选择题:本题共12小题,每小题5分,共60分。在每小题...