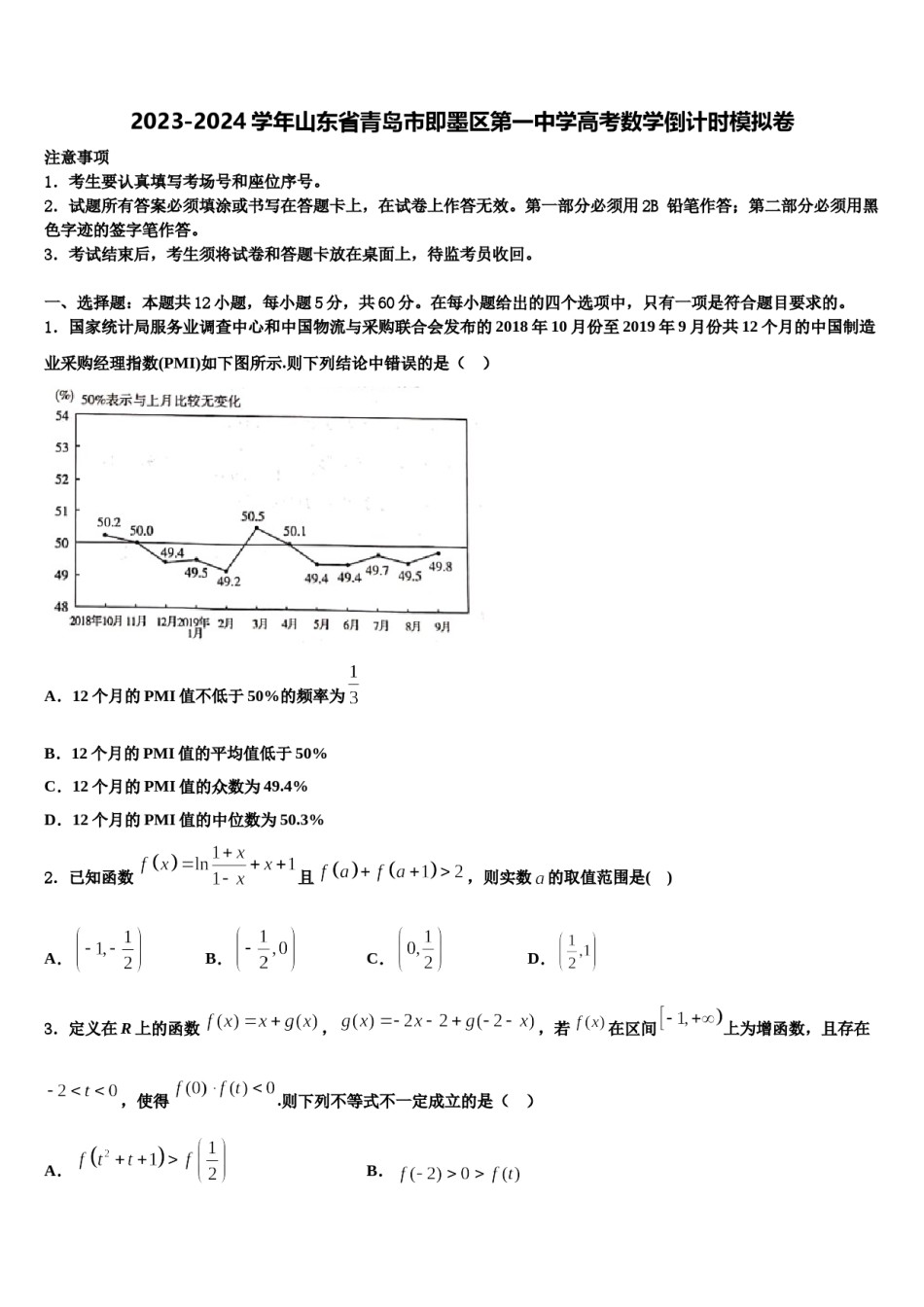
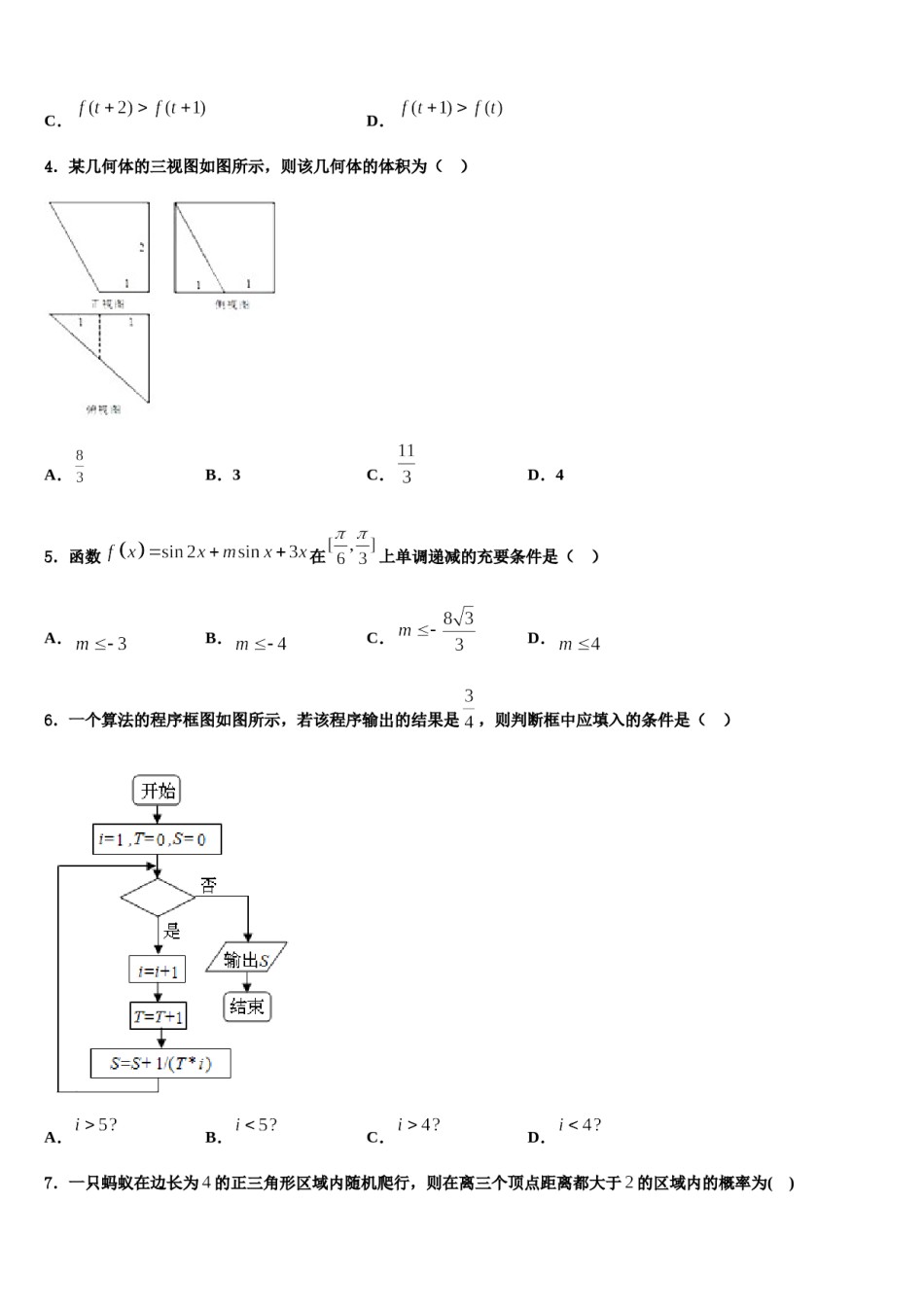
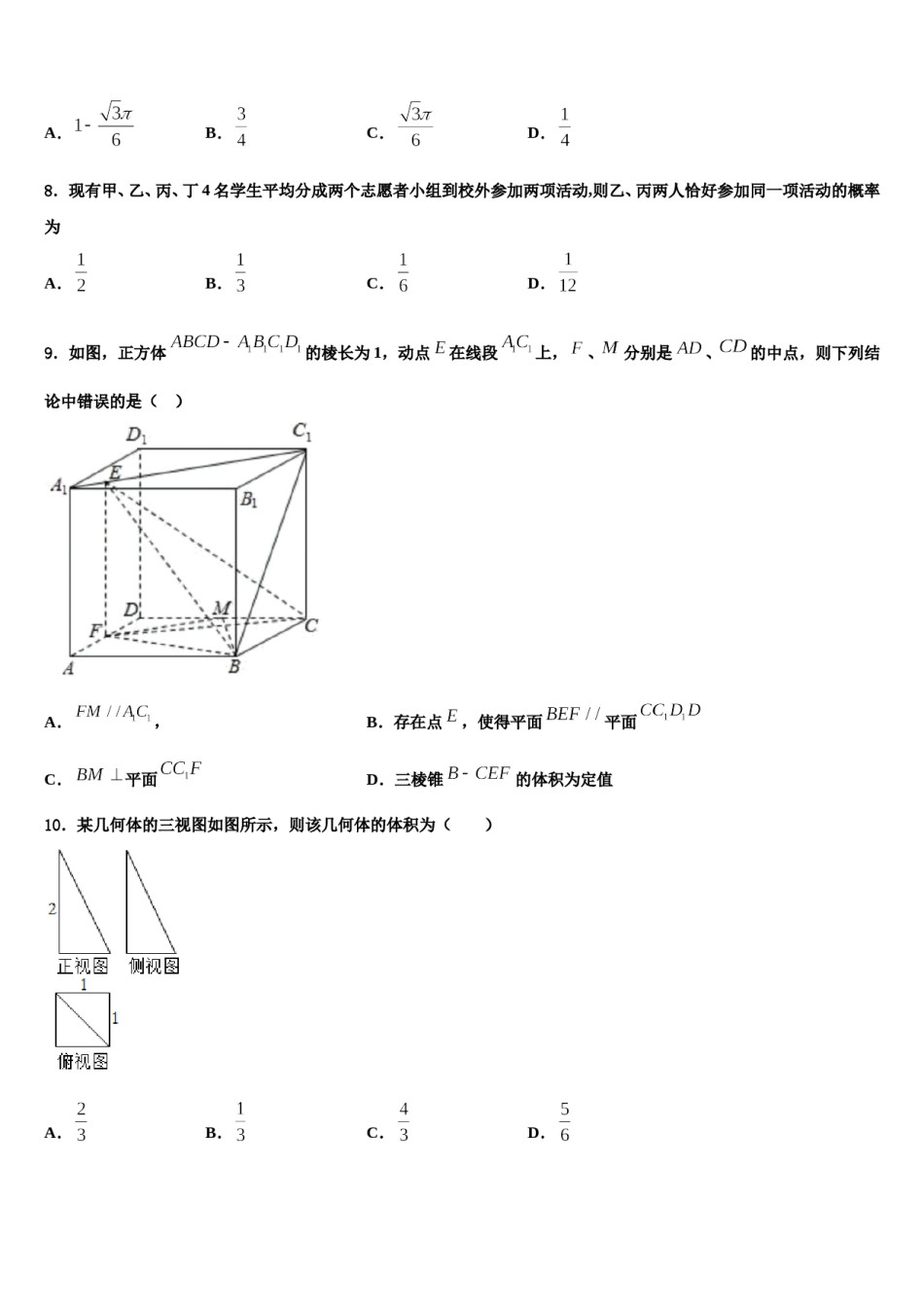
2023-2024学年山东省青岛市即墨区第一中学高考数学倒计时模拟卷注意事项铅笔作答;第二部分必须用黑1.考生要认真填写考场号和座位序号。2.试题所有答案必须填涂或书写在答题卡上,在试卷上作答无效。第一部分必须用2B色字迹的签字笔作答。3.考试结束后,考生须将试卷和答题卡放在桌面上,待监考员收回。一、选择题:本题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的。1.国家统计局服务业调查中心和中国物流与采购联合会发布的2018年10月份至2019年9月份共12个月的中国制造业采购经理指数(PMI)如下图所示.则下列结论中错误的是()A.12个月的PMI值不低于50%的频率为B.12个月的PMI值的平均值低于50%C.12个月的PMI值的众数为49.4%D.12个月的PMI值的中位数为50.3%2.已知函数且,则实数的取值范围是()A.B.C.D.,,若在区间3.定义在R上的函数上为增函数,且存在,使得.则下列不等式不一定成立的是()A.B.C.D.4.某几何体的三视图如图所示,则该几何体的体积为()A.B.3C.D.45.函数在上单调递减的充要条件是()A.B.C.D.6.一个算法的程序框图如图所示,若该程序输出的结果是,则判断框中应填入的条件是()A.B.C.D.7.一只蚂蚁在边长为的正三角形区域内随机爬行,则在离三个顶点距离都大于的区域内的概率为()A.B.C.D.8.现有甲、乙、丙、丁4名学生平均分成两个志愿者小组到校外参加两项活动,则乙、丙两人恰好参加同一项活动的概率为A.B.C.D.9.如图,正方体的棱长为1,动点在线段上,、分别是、的中点,则下列结论中错误的是()A.,B.存在点,使得平面平面C.平面D.三棱锥的体积为定值10.某几何体的三视图如图所示,则该几何体的体积为()A.B.C.D.11.设是定义在实数集上的函数,满足条件是偶函数,且当时,,则,,的大小关系是()A.B.C.D.12.的展开式中含的项的系数为()A.B.60C.70D.80的焦点,则双曲线的标准方程为______.二、填空题:本题共4小题,每小题5分,共20分。13.已知双曲线的一条渐近线为,且经过抛物线14.设函数,,其中.若存在唯一的整数使得,则实数的取值范围是_____.15.已知函数,若,则___________.16.已知在等差数列中,,,前n项和为,则________.三、解答题:共70分。解答应写出文字说明、证明过程或演算步骤。17.(12分)已知,均为正项数列,其前项和分别为,,且,,,当,时,,.(1)求数列,的通项公式;(2)设,求数列的前项和.18.(12分)已知.(1)求不等式的解集;(2)若存在,使得成立,求实数的取值范围19.(12分)如图,在三棱柱中,已知四边形为矩形,,,,的角平分线交于.(1)求证:平面平面;(2)求二面角的余弦值.20.(12分)已知函数()的图象在处的切线为(为自然对数的底数)的值;(1)求(2)若,且对任意恒成立,求的最大值.21.(12分)选修4—5;不等式选讲.已知函数.(1)若的解集非空,求实数的取值范围;(2)若正数满足,为(1)中m可取到的最大值,求证:.22.(10分)已知函数.(Ⅰ)解不等式;在上恰有两个不相等的实数根,求实数的(Ⅱ)设其中为常数.若方程取值范围.参考答案一、选择题:本题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的。1、D【解析】根据图形中的信息,可得频率、平均值的估计、众数、中位数,从而得到答案.【详解】对A,从图中数据变化看,PMI值不低于50%的月份有4个,所以12个月的PMI值不低于50%的频率为,故A正确;对B,由图可以看出,PMI值的平均值低于50%,故B正确;对C,12个月的PMI值的众数为49.4%,故C正确,;对D,12个月的PMI值的中位数为49.6%,故D错误故选:D.【点睛】本题考查频率、平均值的估计、众数、中位数计算,考查数据处理能力,属于基础题.2、B【解析】构造函数,判断出的单调性和奇偶性,由此求得不等式的解集.【详解】构造函数,由解得,所以的定义域为,且,所以为奇函数,而,所以在定义域上为增函数,且.由得,即,所以.故选:B【点睛】本小题主要考查利用函数的单调性和奇偶性解不等式,属于中档题.3、D【解析】根据题...