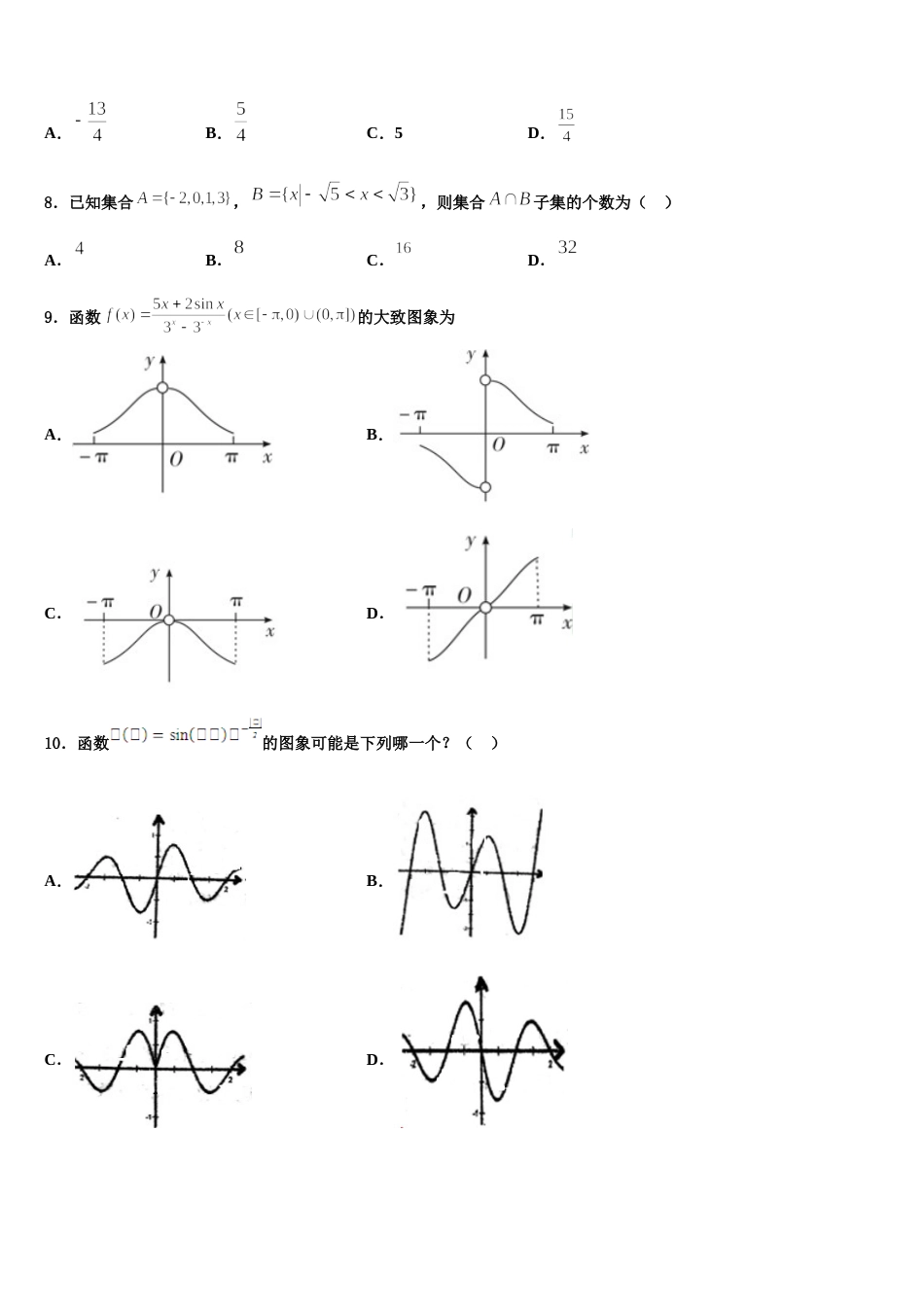
2023-2024 学年山西省同煤二中高三适应性调研考试数学试题注意事项:1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其它答案标号。回答非选择题时,将答案写在答题卡上,写在本试卷上无效。3.考试结束后,将本试卷和答题卡一并交回。一、选择题:本题共 12 小题,每小题 5 分,共 60 分。在每小题给出的四个选项中,只有一项是符合题目要求的。1.设集合则( )A.B.C.D.2.已知函数满足,且,则不等式的解集为( )A.B.C.D.3.抛物线的焦点 是双曲线的右焦点,点 是曲线的交点,点 在抛物线的准线上,是以点 为直角顶点的等腰直角三角形,则双曲线的离心率为( )A.B.C.D.4.若的展开式中含有常数项,且的最小值为,则( )A.B.C.D.5.若各项均为正数的等比数列满足,则公比( )A.1B.2C.3D.46.若复数满足,其中 为虚数单位,是的共轭复数,则复数( )A.B.C.4D.57.在菱形中,,,,分别为,的中点,则( )A.B.C.5D.8.已知集合,,则集合子集的个数为( )A.B.C.D.9.函数的大致图象为A.B.C.D.10.函数的图象可能是下列哪一个?( )A.B.C.D.11.已知,则( )A.2B.C.D.312.已知定义在上的偶函数,当时,,设,则( )A.B.C.D.二、填空题:本题共 4 小题,每小题 5 分,共 20 分。13.用数字、 、、、、组成无重复数字的位自然数,其中相邻两个数字奇偶性不同的有_____个.14.已知双曲线的两条渐近线方程为,若顶点到渐近线的距离为 1,则双曲线方程为 .15.如图,在中,,,,点在边上,且,将射线绕着逆时针方向旋转,并在所得射线上取一点,使得,连接,则的面积为__________.16.在边长为的菱形中,点在菱形所在的平面内.若,则_____.三、解答题:共 70 分。解答应写出文字说明、证明过程或演算步骤。17.(12 分)某机构组织的家庭教育活动上有一个游戏,每次由一个小孩与其一位家长参与,测试家长对小孩饮食习惯的了解程度.在每一轮游戏中,主持人给出 A,B,C,D 四种食物,要求小孩根据自己的喜爱程度对其排序,然后由家长猜测小孩的排序结果.设小孩对四种食物排除的序号依次为 xAxBxCxD,家长猜测的序号依次为 yAyByCyD,其中xAxBxCxD和 yAyByCyD都是 1,2,3,4 四个数字的一种排列.定义随机变量 X=(xA﹣yA)2+(xB﹣yB)2+(xC﹣yC)2+(xD﹣yD)2,用 X 来衡量家长对小孩饮食习惯的了解程度.(1)若参与游戏的家长对小孩的饮食习惯完全不了解.(ⅰ)求他们在一轮游戏中,对四种食物排出的序号完全不同的概率;(ⅱ)求 X 的分布列(简要说明方法,不用写出详细计算过程);(2)若有一组小孩和家长进行来三轮游戏,三轮的结果都满足 X<4,请判断这位家长对小孩饮食习惯是否了解,说明理由.18.(12 分)如图,在直角梯形中,,,,为的中点,沿将折起,使得点到点位置,且,为的中点,是上的动点(与点,不重合).(Ⅰ)证明:平面平面垂直;(Ⅱ)是否存在点,使得二面角的余弦值?若存在,确定点位置;若不存在,说明理由.19.(12 分)在中,,.已知分别是的中点.将沿折起,使到的位置且二面角的大小是 60°,连接,如图:(1)证明:平面平面(2)求平面与平面所成二面角的大小.20.(12 分)已知函数,其中.(1)讨论函数的零点个数;(2)求证:.21.(12 分)已知函数,设为的导数,.(1)求,; (2)猜想的表达式,并证明你的结论.22.(10 分)已知在中,内角所对的边分别为,若,,且.(1)求的值;(2)求的面积.参考答案一、选择题:本题共 12 小题,每小题 5 分,共 60 分。在每小题给出的四个选项中,只有一项是符合题目要求的。1、C【解析】直接求交集得到答案.【详解】集合,则.故选:.【点睛】本题考查了交集运算,属于简单题.2、B【解析】构造函数,利用导数研究函数的单调性,即可得到结论.【详解】设,则函数的导数,,,即函数为减函数,,,则不等式等价为,则不等式的解集为,即...