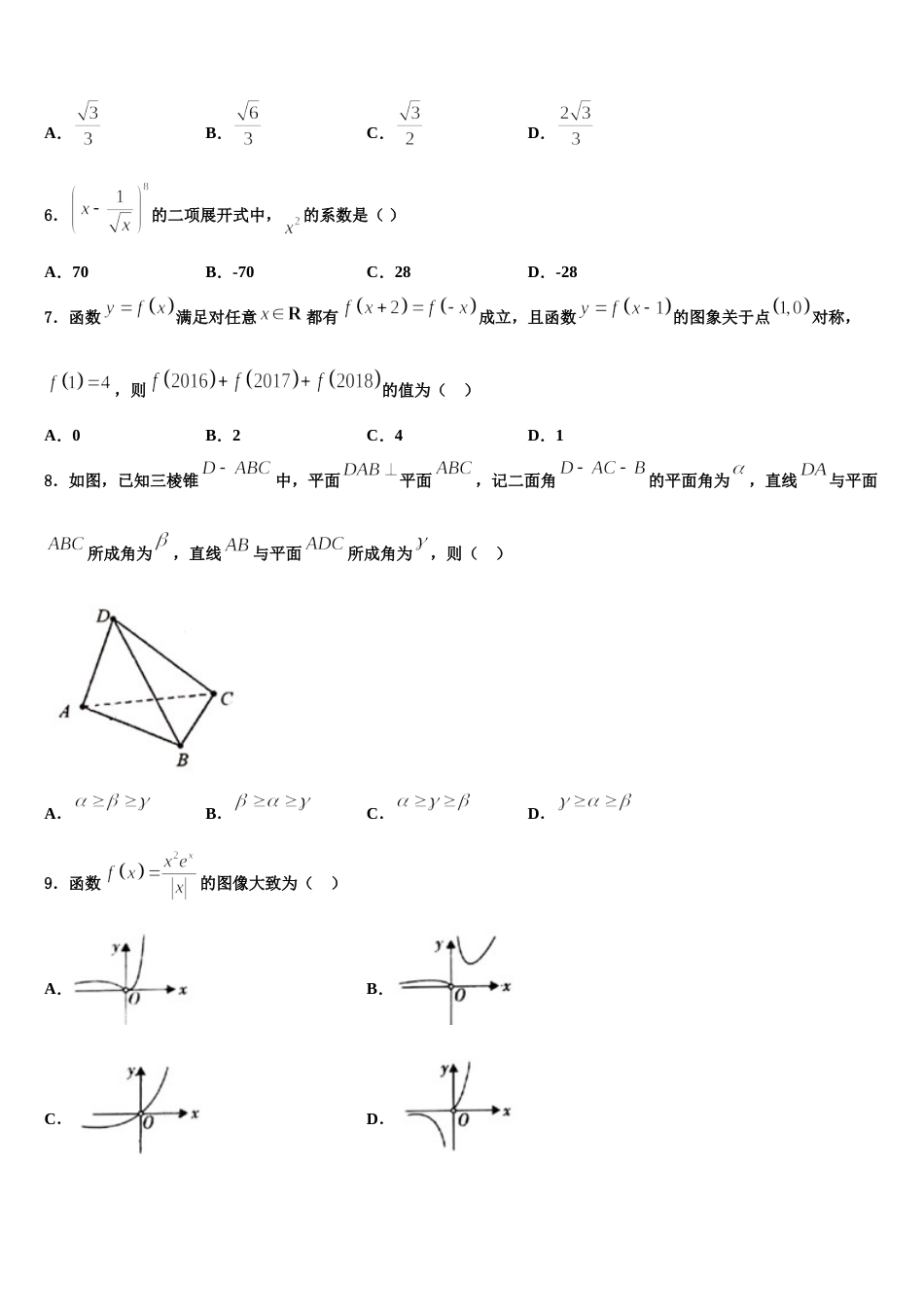
2023-2024 学年山西省吕梁市柳林县高三下学期联考数学试题注意事项1.考试结束后,请将本试卷和答题卡一并交回.2.答题前,请务必将自己的姓名、准考证号用 0.5 毫米黑色墨水的签字笔填写在试卷及答题卡的规定位置.3.请认真核对监考员在答题卡上所粘贴的条形码上的姓名、准考证号与本人是否相符.4.作答选择题,必须用 2B 铅笔将答题卡上对应选项的方框涂满、涂黑;如需改动,请用橡皮擦干净后,再选涂其他答案.作答非选择题,必须用 05 毫米黑色墨水的签字笔在答题卡上的指定位置作答,在其他位置作答一律无效.5.如需作图,须用 2B 铅笔绘、写清楚,线条、符号等须加黑、加粗.一、选择题:本题共 12 小题,每小题 5 分,共 60 分。在每小题给出的四个选项中,只有一项是符合题目要求的。1.已知函数的图像上有且仅有四个不同的点关于直线的对称点在的图像上,则实数的取值范围是( )A.B.C.D.2.已知,,若,则实数的值是( )A.-1B.7C.1D.1 或 73.已知双曲线,过原点作一条倾斜角为直线分别交双曲线左、右两支 P,Q 两点,以线段PQ 为直径的圆过右焦点 F,则双曲线离心率为 A.B.C.2D.4.函数的最大值为,最小正周期为,则有序数对为( )A.B.C.D.5.已知双曲线的一条渐近线方程是,则双曲线的离心率为( )A.B.C.D.6.的二项展开式中,的系数是( )A.70B.-70C.28D.-287.函数满足对任意都有成立,且函数的图象关于点对称,,则的值为( )A.0B.2C.4D.18.如图,已知三棱锥中,平面平面,记二面角的平面角为,直线与平面所成角为,直线与平面所成角为,则( )A.B.C.D.9.函数的图像大致为( )A.B.C.D.10.已知双曲线的左,右焦点分别为,O 为坐标原点,P 为双曲线在第一象限上的点,直线 PO,分别交双曲线 C 的左,右支于另一点,且,则双曲线的离心率为( )A.B.3C.2D.11.公元 263 年左右,我国数学家刘徽发现当圆内接正多边形的边数无限增加时,多边形面积可无限逼近圆的面积,并创立了“割圆术”,利用“割圆术”刘徽得到了圆周率精确到小数点后两位的近似值,这就是著名的“徽率”。如图是利用刘徽的“割圆术”思想设计的一个程序框图,则输出的值为( )(参考数据: )A.48B.36C.24D.1212.已知不同直线 、与不同平面、,且,,则下列说法中正确的是( )A.若,则B.若,则C.若,则D.若,则二、填空题:本题共 4 小题,每小题 5 分,共 20 分。13.的展开式中的常数项为_______.14.将一个半径适当的小球放入如图所示的容器最上方的入口处,小球将自由下落.小球在下落的过程中,将 3 次遇到黑色障碍物,最后落入袋或袋中.己知小球每次遇到黑色障碍物时,向左、右两边下落的概率都是,则小球落入袋中的概率为__________.15.若函数在区间上有且仅有一个零点,则实数的取值范围有___________.16.已知一个正四棱锥的侧棱与底面所成的角为,侧面积为,则该棱锥的体积为__________.三、解答题:共 70 分。解答应写出文字说明、证明过程或演算步骤。17.(12 分)已知数列为公差为 d 的等差数列,,,且,,依次成等比数列,.(1)求数列的前 n 项和;(2)若,求数列的前 n 项和为.18.(12 分)为了解广大学生家长对校园食品安全的认识,某市食品安全检测部门对该市家长进行了一次校园食品安全网络知识问卷调查,每一位学生家长仅有一次参加机会,现对有效问卷进行整理,并随机抽取出了 200 份答卷,统计这些答卷的得分(满分:100 分)制出的频率分布直方图如图所示,由频率分布直方图可以认为,此次问卷调查的得分服从正态分布,其中近似为这 200 人得分的平均值(同一组数据用该组区间的中点值作为代表).(1)请利用正态分布的知识求;(2)该市食品安全检测部门为此次参加问卷调查的学生家长制定如下奖励方案:① 得分不低于的可以获赠 2 次随机话费,得分低于的可以获赠 1 次随机话费:② 每次获赠的随机话费和对应的概率为:获赠的随机话费(单位:元)概率市食品安全检测部门预计参加此次活动的家长约 5000 人,请依据以上...