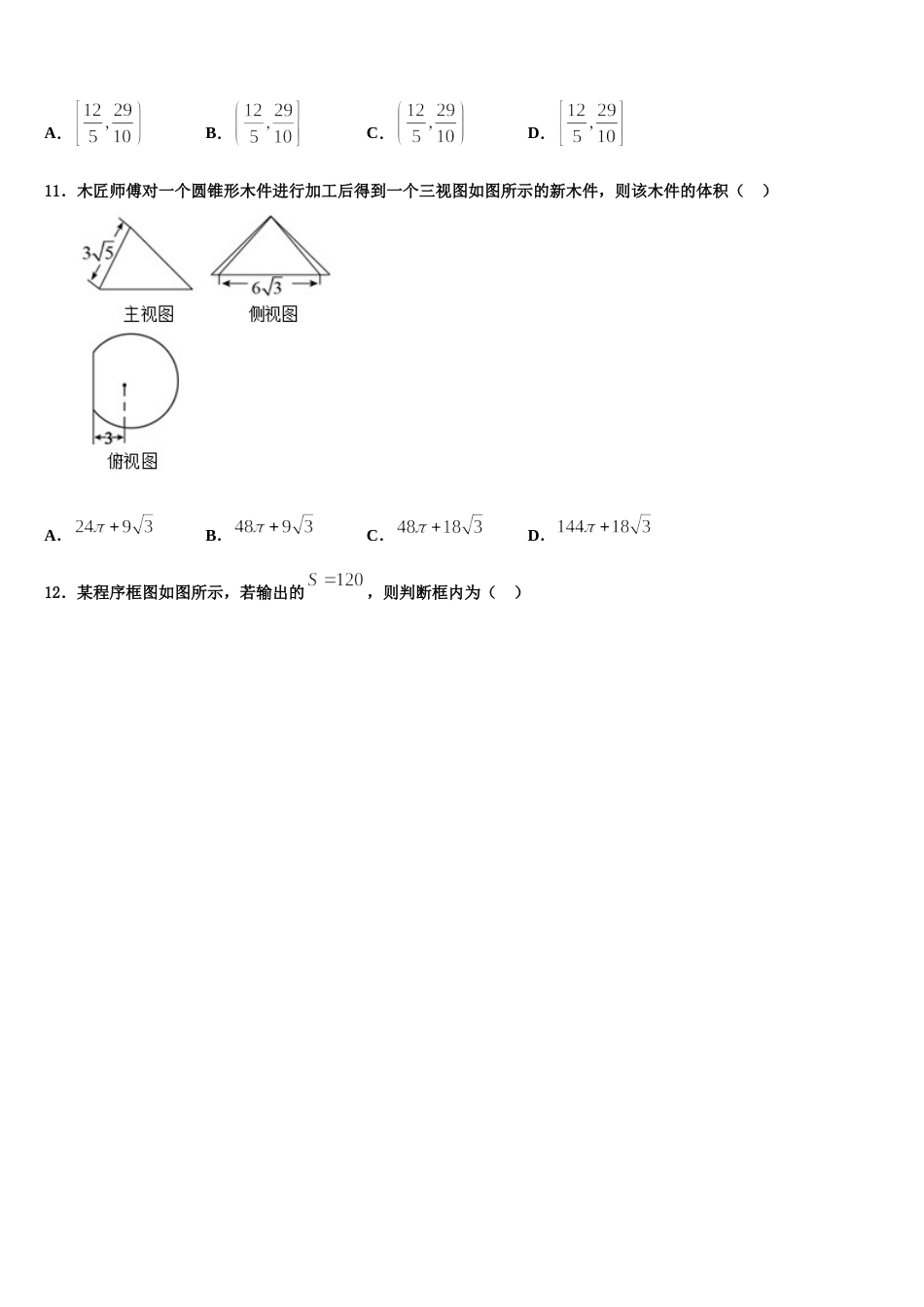
2023-2024 学年岳阳市重点中学高考冲刺模拟数学试题注意事项1.考试结束后,请将本试卷和答题卡一并交回.2.答题前,请务必将自己的姓名、准考证号用 0.5 毫米黑色墨水的签字笔填写在试卷及答题卡的规定位置.3.请认真核对监考员在答题卡上所粘贴的条形码上的姓名、准考证号与本人是否相符.4.作答选择题,必须用 2B 铅笔将答题卡上对应选项的方框涂满、涂黑;如需改动,请用橡皮擦干净后,再选涂其他答案.作答非选择题,必须用 05 毫米黑色墨水的签字笔在答题卡上的指定位置作答,在其他位置作答一律无效.5.如需作图,须用 2B 铅笔绘、写清楚,线条、符号等须加黑、加粗.一、选择题:本题共 12 小题,每小题 5 分,共 60 分。在每小题给出的四个选项中,只有一项是符合题目要求的。1.蒙特卡洛算法是以概率和统计的理论、方法为基础的一种计算方法,将所求解的问题同一定的概率模型相联系;用均匀投点实现统计模拟和抽样,以获得问题的近似解,故又称统计模拟法或统计实验法.现向一边长为的正方形模型内均匀投点,落入阴影部分的概率为,则圆周率( )A.B.C.D.2.设,是非零向量,若对于任意的,都有成立,则A.B.C.D.3.已知函数,则下列结论中正确的是① 函数的最小正周期为;② 函数的图象是轴对称图形;③ 函数的极大值为;④ 函数的最小值为.A.①③B.②④C.②③D.②③④4.设,,,则,,三数的大小关系是A.B.C.D.5.复数( 为虚数单位),则等于( )A.3B.C.2D.6.在平面直角坐标系中,已知点,,若动点满足 ,则的取值范围是( )A.B.C.D.7.由曲线 y=x2与曲线 y2=x 所围成的平面图形的面积为( )A.1B.C.D.8.已知是平面内互不相等的两个非零向量,且与的夹角为,则的取值范围是( )A.B.C.D.9.已知函数是偶函数,当时,函数单调递减,设,,,则的大小关系为()A.B.C.D.10.设函数,若在上有且仅有 5 个零点,则的取值范围为( )A.B.C.D.11.木匠师傅对一个圆锥形木件进行加工后得到一个三视图如图所示的新木件,则该木件的体积( ) A.B.C.D.12.某程序框图如图所示,若输出的,则判断框内为( )A.B.C.D.二、填空题:本题共 4 小题,每小题 5 分,共 20 分。13.已知圆柱的两个底面的圆周在同一个球的球面上,圆柱的高和球半径均为 2,则该圆柱的底面半径为__________.14.已知实数满约束条件,则的最大值为___________.15.三棱锥中,点是斜边上一点.给出下列四个命题:① 若平面,则三棱锥的四个面都是直角三角形;② 若,,,平面,则三棱锥的外接球体积为;③ 若,,,在平面上的射影是内心,则三棱锥的体积为 2;④ 若,,,平面,则直线与平面所成的最大角为.其中正确命题的序号是__________.(把你认为正确命题的序号都填上)16.将函数的图像向右平移个单位,得到函数的图像,则函数在区间上的值域为__________.三、解答题:共 70 分。解答应写出文字说明、证明过程或演算步骤。17.(12 分)已知函数(为实常数).(1)讨论函数在上的单调性;(2)若存在,使得成立,求实数的取值范围.18.(12 分)记函数的最小值为.(1)求的值;(2)若正数,,满足,证明:.19.(12 分)已知函数.(1)当时,求不等式的解集;(2)若关于的不等式的解集包含,求实数的取值范围.20.(12 分)设,函数,其中 为自然对数的底数.(1)设函数.① 若,试判断函数与的图像在区间上是否有交点;② 求证:对任意的,直线都不是的切线;(2)设函数,试判断函数是否存在极小值,若存在,求出的取值范围;若不存在,请说明理由.21.(12 分)已知的内角,,的对边分别为,,,且.(1)求;(2)若的面积为,,求的周长.22.(10 分)已知多面体中,、均垂直于平面,,,,是的中点.(1)求证:平面;(2)求直线与平面所成角的正弦值.参考答案一、选择题:本题共 12 小题,每小题 5 分,共 60 分。在每小题给出的四个选项中,只有一项是符合题目要求的。1、A【解析】计算出黑色部分的面积与总面积的比,即可得解.【详解】由,∴.故选:A【点睛】...