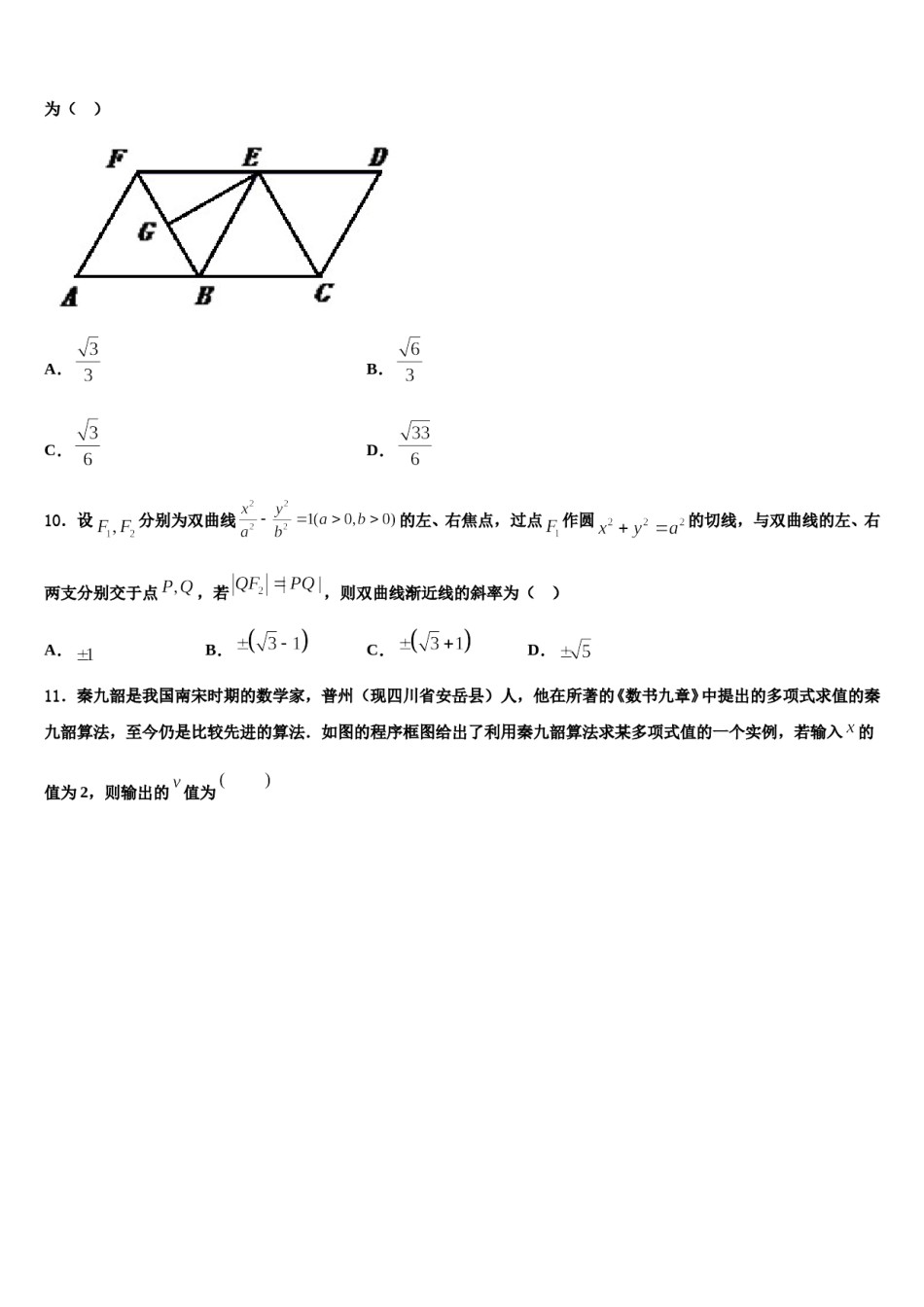
2023-2024学年广东省佛山市石门中学高考冲刺模拟数学试题请考生注意:1.请用2B铅笔将选择题答案涂填在答题纸相应位置上,请用0.5毫米及以上黑色字迹的钢笔或签字笔将主观题的答案写在答题纸相应的答题区内。写在试题卷、草稿纸上均无效。2.答题前,认真阅读答题纸上的《注意事项》,按规定答题。一、选择题:本题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的。1.复数的虚部为()A.B.C.2D.2.已知平面向量,,,则实数x的值等于()A.6B.1C.D.3.设,点,,,,设对一切都有不等式成立,则正整数的最小值为()A.B.C.D.侧棱,直角边AE绕斜边AB旋转,则在旋转的过程中,有下4.等腰直角三角形的斜边AB为正四面体列说法:(1)四面体EBCD的体积有最大值和最小值;(2)存在某个位置,使得;(3)设二面角的平面角为,则;(4)AE的中点M与AB的中点N连线交平面BCD于点P,则点P的轨迹为椭圆.其中,正确说法的个数是()A.1B.2C.3D.45.若(是虚数单位),则的值为()A.3B.5C.D.6.设集合A={yy=2x﹣1,x∈R},B={x﹣2≤x≤3,x∈Z},则A∩B=()A.(﹣1,3]B.[﹣1,3]C.{0,1,2,3}D.{﹣1,0,1,2,3}7.蒙特卡洛算法是以概率和统计的理论、方法为基础的一种计算方法,将所求解的问题同一定的概率模型相联系;用均匀投点实现统计模拟和抽样,以获得问题的近似解,故又称统计模拟法或统计实验法.现向一边长为的正方形模型内均匀投点,落入阴影部分的概率为,则圆周率()A.B.C.D.8.若执行如图所示的程序框图,则输出的值是()A.B.C.D.49.下图为一个正四面体的侧面展开图,为的中点,则在原正四面体中,直线与直线所成角的余弦值为()A.B.C.D.10.设分别为双曲线的左、右焦点,过点作圆的切线,与双曲线的左、右两支分别交于点,若,则双曲线渐近线的斜率为()A.B.C.D.11.秦九韶是我国南宋时期的数学家,普州(现四川省安岳县)人,他在所著的《数书九章》中提出的多项式求值的秦九韶算法,至今仍是比较先进的算法.如图的程序框图给出了利用秦九韶算法求某多项式值的一个实例,若输入的值为2,则输出的值为A.B.C.D.12.已知复数(为虚数单位),则下列说法正确的是()A.的虚部为B.复数在复平面内对应的点位于第三象限C.的共轭复数D.二、填空题:本题共4小题,每小题5分,共20分。13.若满足约束条件,则的最大值为__________.14.二项式的展开式的各项系数之和为_____,含项的系数为_____.15.若正实数,,满足,则的最大值是__________.16.设双曲线的左焦点为,过点且倾斜角为45°的直线与双曲线的两条渐近线顺次交于,两点若,则的离心率为________.三、解答题:共70分。解答应写出文字说明、证明过程或演算步骤。17.(12分)以坐标原点为极点,轴正半轴为极轴建立极坐标系,曲线的极坐标方程是,直线和直线的极坐标方程分别是()和(),其中().(1)写出曲线的直角坐标方程;的面积最小值.(2)设直线和直线分别与曲线交于除极点的另外点,,求18.(12分)设椭圆的离心率为,左、右焦点分别为,点D在椭圆C上,的周长为.(1)求椭圆C的标准方程;(2)过圆上任意一点P作圆E的切线l,若l与椭圆C交于A,B两点,O为坐标原点,求证:为定值.19.(12分)某商场为改进服务质量,在进场购物的顾客中随机抽取了人进行问卷调查.调查后,就顾客“购物体验”的满意度统计如下:满意不满意男女是否有的把握认为顾客购物体验的满意度与性别有关?若在购物体验满意的问卷顾客中按照性别分层抽取了人发放价值元的购物券.若在获得了元购物券的人中随机抽取人赠其纪念品,求获得纪念品的人中仅有人是女顾客的概率.附表及公式:.20.(12分)已知函数,其中.(1)函数在处的切线与直线垂直,求实数的值;(2)若函数在定义域上有两个极值点,且.①求实数的取值范围;②求证:.21.(12分)在平面四边形(图①)中,与均为直角三角形且有公共斜边,设,∠,∠,将沿折起,构成如图②所示的三棱锥,且使=.(1)求证:平面⊥平面;(2)求二面角的余弦值.22.(10分)甲、乙两班各派...