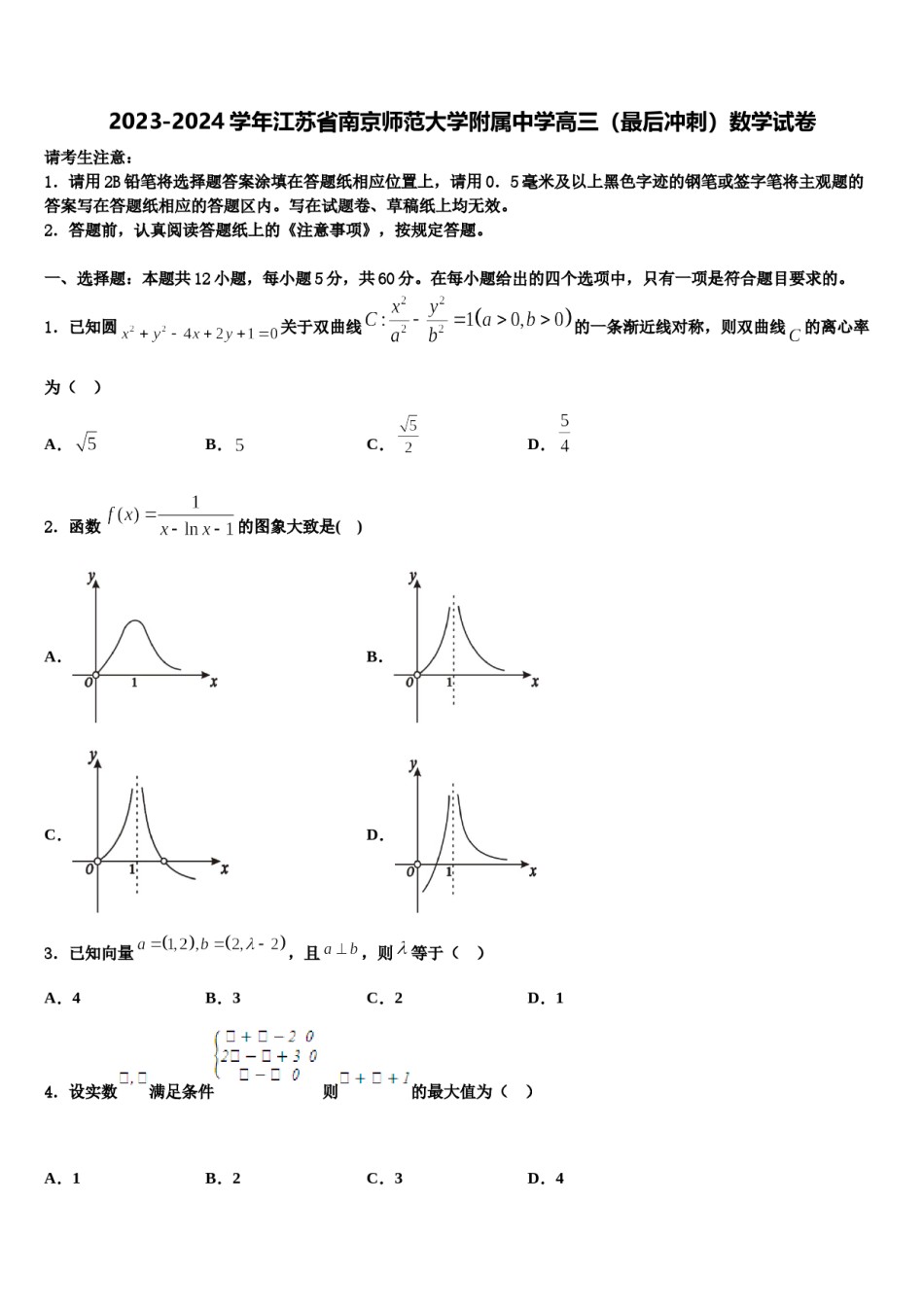
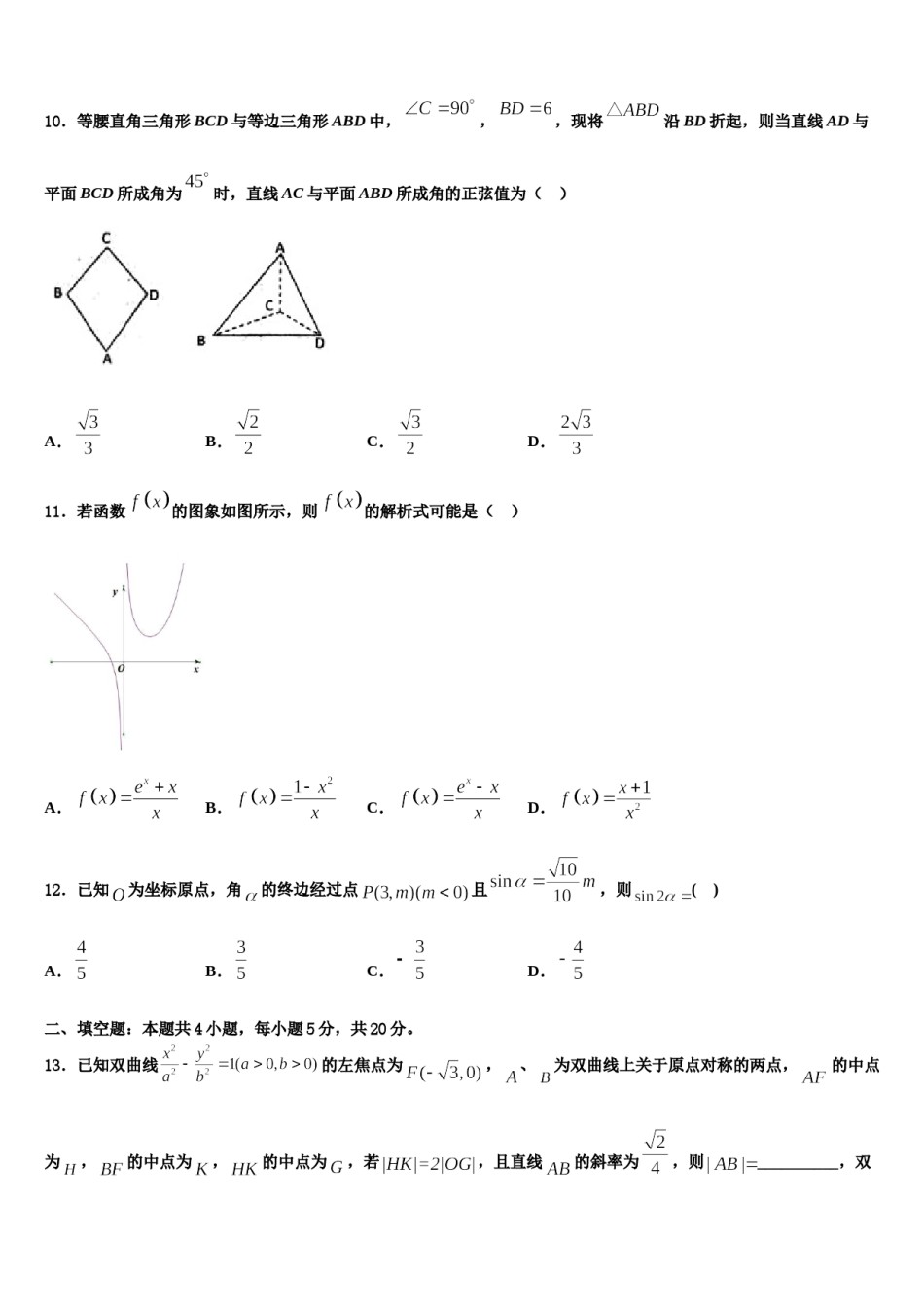
2023-2024学年江苏省南京师范大学附属中学高三(最后冲刺)数学试卷请考生注意:1.请用2B铅笔将选择题答案涂填在答题纸相应位置上,请用0.5毫米及以上黑色字迹的钢笔或签字笔将主观题的答案写在答题纸相应的答题区内。写在试题卷、草稿纸上均无效。2.答题前,认真阅读答题纸上的《注意事项》,按规定答题。一、选择题:本题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的。1.已知圆关于双曲线的一条渐近线对称,则双曲线的离心率为()A.B.C.D.2.函数的图象大致是()A.B.C.D.3.已知向量,且,则等于()A.4B.3C.2D.14.设实数满足条件则的最大值为()A.1B.2C.3D.45.已知双曲线的左右焦点分别为,,以线段为直径的圆与双曲线在第二象限的交点为,若直线与圆相切,则双曲线的渐近线方程是()A.B.C.D.)的一个零点是,函数6.已知函数(,图象的一条对称轴是直线,则当取得最小值时,函数的单调递增区间是()A.()B.()C.()D.()7.已知函数,为的零点,为图象的对称轴,且在区间上单调,则的最大值是()A.8.设双曲线B.C.D.()A.的一条渐近线为,且一个焦点与抛物线的焦点相同,则此双曲线的方程为B.C.D.9.设为虚数单位,为复数,若为实数,则()A.B.C.D.10.等腰直角三角形BCD与等边三角形ABD中,,,现将沿BD折起,则当直线AD与平面BCD所成角为时,直线AC与平面ABD所成角的正弦值为()A.B.C.D.11.若函数的图象如图所示,则的解析式可能是()A.B.C.D.12.已知为坐标原点,角的终边经过点且,则()A.B.C.D.,、为双曲线上关于原点对称的两点,的中点二、填空题:本题共4小题,每小题5分,共20分。13.已知双曲线的左焦点为为,的中点为,的中点为,若,且直线的斜率为,则__________,双曲线的离心率为__________.=(-3,1),则=______.14.已知向量=(1,2),15.已知是同一球面上的四个点,其中平面,是正三角形,,则该球的表面积为______.16.四边形中,,,,,则的最小值是______.三、解答题:共70分。解答应写出文字说明、证明过程或演算步骤。名高三学生平均每天体育锻炼时间进17.(12分)某中学为研究学生的身体素质与体育锻炼时间的关系,对该校行调查,如表:(平均每天锻炼的时间单位:分钟)将学生日均体育锻炼时间在的学生评价为“锻炼达标”.(1)请根据上述表格中的统计数据填写下面列联表:并通过计算判断,是否能在犯错误的概率不超过的前提下认为“锻炼达标”与性别有关?(2)在“锻炼达标”的学生中,按男女用分层抽样方法抽出人,进行体育锻炼体会交流.(i)求这人中,男生、女生各有多少人?(ii)从参加体会交流的人中,随机选出人发言,记这人中女生的人数为,求的分布列和数学期望.参考公式:,其中.临界值表:0.050.0250.0100.1002.7063.8415.0246.63518.(12分)在四棱锥中,底面是平行四边形,底面.(1)证明:;(2)求二面角的正弦值.19.(12分)已知椭圆的焦距为2,且过点.(1)求椭圆的方程;(2)设为的左焦点,点为直线上任意一点,过点作的垂线交于两点,(ⅰ)证明:平分线段(其中为坐标原点);(ⅱ)当取最小值时,求点的坐标.20.(12分)设数列,其前项和,又单调递增的等比数列,,.(Ⅰ)求数列,的通项公式;(Ⅱ)若,求数列的前n项和,并求证:.21.(12分)已知函数.(1)若函数,求的极值;(2)证明:(参考数据:.)22.(10分)在平面直角坐标系中,已知直线l的参数方程为(t为参数),在以坐标原点O为极点,x轴的正半轴为极轴,且与直角坐标系长度单位相同的极坐标系中,曲线C的极坐标方程是.(1)求直线l的普通方程与曲线C的直角坐标方程;(2)若直线l与曲线C相交于两点A,B,求线段的长.参考答案一、选择题:本题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的。1、C【解析】将圆,化为标准方程为,求得圆心为.根据圆关于双曲线的一条渐近线对称,则圆心在渐近线上,.再根据求解.【详解】,已知圆所以其标准方程为:,所以圆心为.因为双曲线,所以其渐近线方程为...