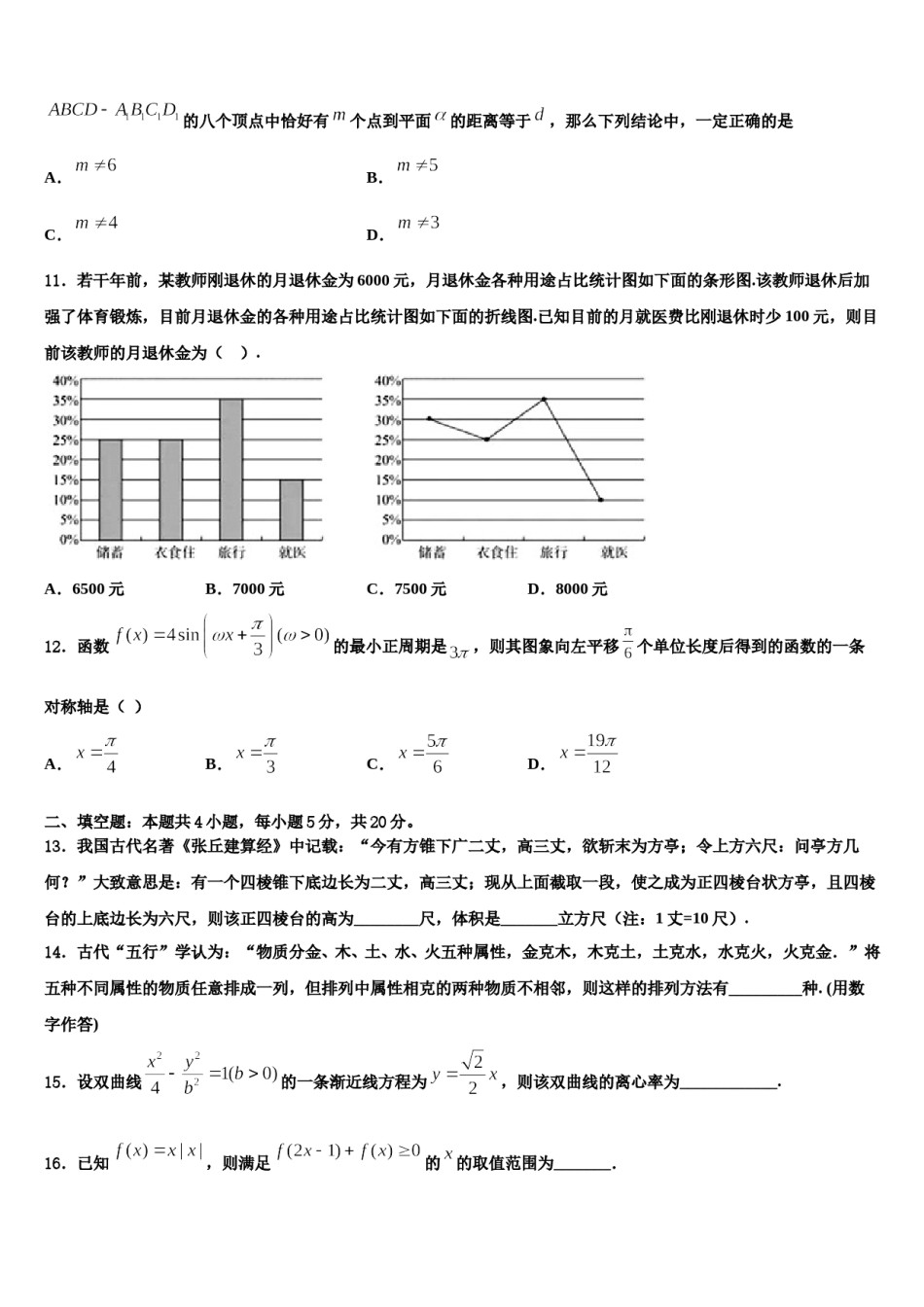
2023-2024学年江西南昌十所重点中学高三第二次调研数学试卷注意事项铅笔作答;第二部分必须用黑1.考生要认真填写考场号和座位序号。2.试题所有答案必须填涂或书写在答题卡上,在试卷上作答无效。第一部分必须用2B色字迹的签字笔作答。3.考试结束后,考生须将试卷和答题卡放在桌面上,待监考员收回。一、选择题:本题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的。1.如图是甲、乙两位同学在六次数学小测试(满分100分)中得分情况的茎叶图,则下列说法错误的是()A.甲得分的平均数比乙大B.甲得分的极差比乙大C.甲得分的方差比乙小D.甲得分的中位数和乙相等2.设函数在上可导,其导函数为,若函数在处取得极大值,则函数的图象可能是()A.B.C.D.3.关于的不等式的解集是,则关于的不等式的解集是()A.B.C.D.4.若的二项式展开式中二项式系数的和为32,则正整数的值为()A.75.函数B.6C.5D.4的图象大致为()A.B.C.D.6.设,则,则()A.B.C.D.,则()7.已知全集,A.B.C.D.8.设为的两个零点,且的最小值为1,则()A.B.C.D.9.若非零实数、满足,则下列式子一定正确的是(),如果正方体A.B.C.D.10.已知正方体的棱长为1,平面与此正方体相交.对于实数的八个顶点中恰好有个点到平面的距离等于,那么下列结论中,一定正确的是A.B.C.D.11.若干年前,某教师刚退休的月退休金为6000元,月退休金各种用途占比统计图如下面的条形图.该教师退休后加强了体育锻炼,目前月退休金的各种用途占比统计图如下面的折线图.已知目前的月就医费比刚退休时少100元,则目前该教师的月退休金为().A.6500元B.7000元C.7500元D.8000元12.函数的最小正周期是,则其图象向左平移个单位长度后得到的函数的一条对称轴是()A.B.C.D.二、填空题:本题共4小题,每小题5分,共20分。13.我国古代名著《张丘建算经》中记载:“今有方锥下广二丈,高三丈,欲斩末为方亭;令上方六尺:问亭方几何?”大致意思是:有一个四棱锥下底边长为二丈,高三丈;现从上面截取一段,使之成为正四棱台状方亭,且四棱台的上底边长为六尺,则该正四棱台的高为________尺,体积是_______立方尺(注:1丈=10尺).14.古代“五行”学认为:“物质分金、木、土、水、火五种属性,金克木,木克土,土克水,水克火,火克金.”将五种不同属性的物质任意排成一列,但排列中属性相克的两种物质不相邻,则这样的排列方法有_________种.(用数字作答)15.设双曲线的一条渐近线方程为,则该双曲线的离心率为____________.16.已知,则满足的的取值范围为_______.三、解答题:共70分。解答应写出文字说明、证明过程或演算步骤。17.(12分)正项数列的前n项和Sn满足:(1)求数列的通项公式;(2)令,数列{bn}的前n项和为Tn,证明:对于任意的n∈N,都有Tn<.18.(12分)已知函数,.(1)若不等式对恒成立,求的最小值;(2)证明:.(3)设方程的实根为.令若存在,,,使得,证明:.19.(12分)在平面直角坐标系xOy中,直线l的参数方程为(t为参数),以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,圆C的极坐标方程为.(1)求直线l的普通方程和圆C的直角坐标方程;(2)直线l与圆C交于A,B两点,点P(2,1),求PA⋅PB的值.20.(12分)已知函数.(1)求的单调区间;(2)讨论零点的个数.21.(12分)已知函数.(1)若函数在上单调递减,求实数的取值范围;(2)若,求的最大值.22.(10分)设函数.(1)解不等式;(2)记的最大值为,若实数、、满足,求证:.参考答案一、选择题:本题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的。1、B【解析】由平均数、方差公式和极差、中位数概念,可得所求结论.【详解】对于甲,;对于乙,,乙的极差为,故正确;.5,,故错误;甲的极差为对于甲,方差对于乙,方差,故正确;甲得分的中位数为,乙得分的中位数为,故正确.故选:.【点睛】本题考查茎叶图的应用,考查平均数和方差等概念,培养计算能力,意在考查学生对这些知识的理解掌握水平,属于基础题...