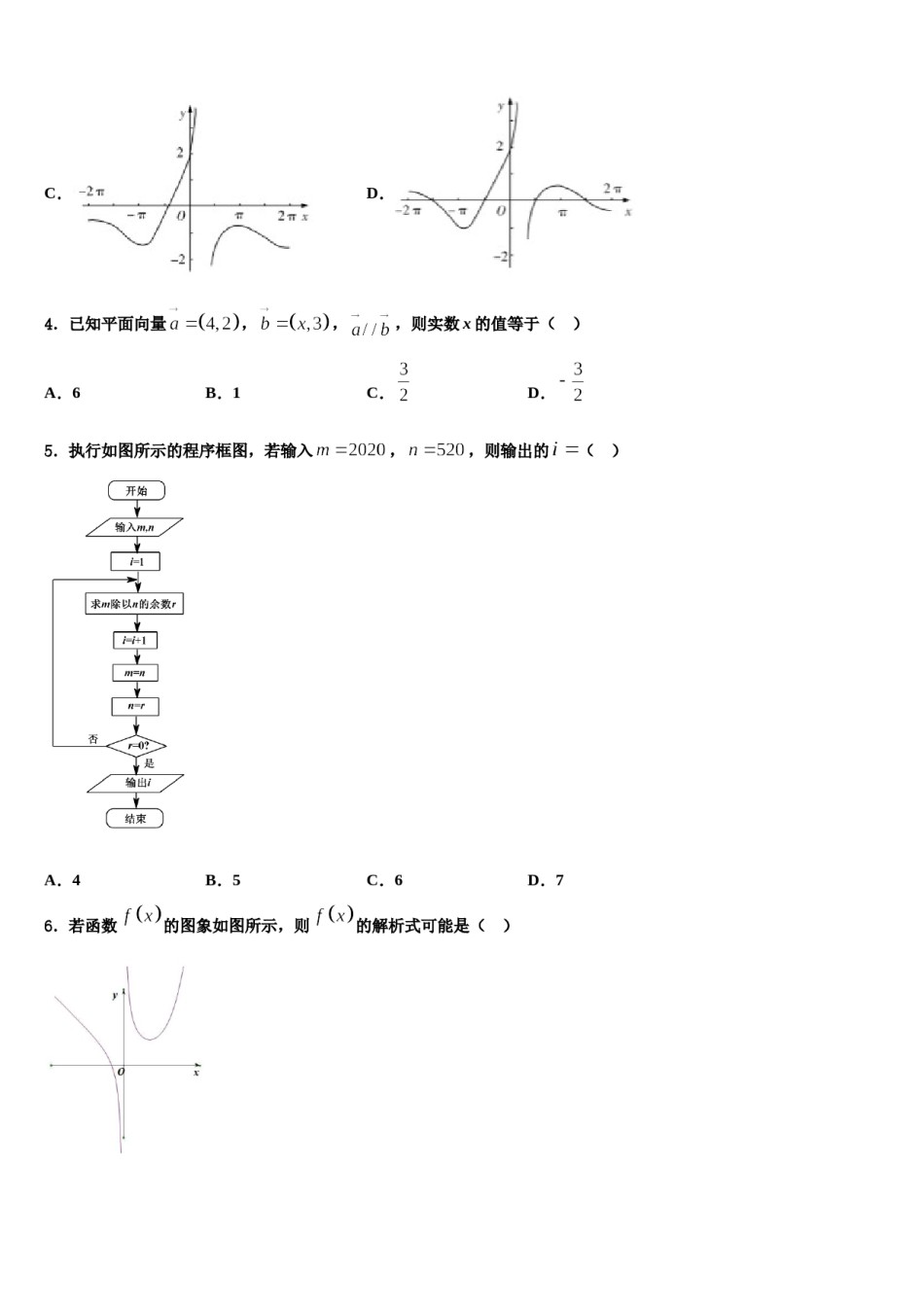
2023-2024学年江西省上高县二中高三六校第一次联考数学试卷考生请注意:1.答题前请将考场、试室号、座位号、考生号、姓名写在试卷密封线内,不得在试卷上作任何标记。2.第一部分选择题每小题选出答案后,需将答案写在试卷指定的括号内,第二部分非选择题答案写在试卷题目指定的位置上。3.考生必须保证答题卡的整洁。考试结束后,请将本试卷和答题卡一并交回。一、选择题:本题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的。1.《算数书》竹简于上世纪八十年代在湖北省江陵县张家山出土,这是我国现存最早的有系统的数学典籍.其中记载有求“囷盖”的术:“置如其周,令相承也.又以高乘之,三十六成一”.该术相当于给出了由圆锥的底面周长与高,计算其体积的近似公式.它实际上是将圆锥体积公式中的圆周率近似取为3.那么近似公式相当于将圆锥体积公式中的圆周率近似取为()A.B.C.D.2.设集合A={4,5,7,9},B={3,4,7,8,9},全集U=AB,则集合中的元素共有()A.3个B.4个C.5个D.6个3.函数在的图象大致为A.B.C.D.4.已知平面向量,,,则实数x的值等于()A.6B.1C.D.,,则输出的()5.执行如图所示的程序框图,若输入A.4B.5C.6D.76.若函数的图象如图所示,则的解析式可能是()A.B.C.D.7.一物体作变速直线运动,其曲线如图所示,则该物体在间的运动路程为()m.A.1B.C.D.28.点在所在的平面内,,,,,且,则()A.B.C.D.9.在平面直角坐标系xOy中,已知椭圆的右焦点为,若F到直线的距离为,则E的离心率为()A.B.C.D.10.已知非零向量,满足,则“”是“”的()D.既不充分也不必要条件解:A.充分不必要条件B.必要不充分条件C.充要条件11.设函数若关于的方程有四个实数解,其中,则的取值范围是()A.B.C.D.12.复数的共轭复数在复平面内所对应的点位于()A.第一象限B.第二象限C.第三象限D.第四象限二、填空题:本题共4小题,每小题5分,共20分。13.已知,则=___________,_____________________________,若,则14.已知________.15.设是定义在上的函数,且,对任意,若经过点的一次函数与轴的交点为,且互不相等,则称为关于函数的平均数,记为.当_________时,为的几何平均数.(只需写出一个符合要求的函数即可)16.已知,,,则的最小值是__.三、解答题:共70分。解答应写出文字说明、证明过程或演算步骤。17.(12分)以平面直角坐标系的原点为极点,轴的正半轴为极轴,且在两种坐标系中取相同的长度单位,建立极坐标系,已知曲线,曲线(为参数),求曲线交点的直角坐标.18.(12分)在四棱锥中,底面为直角梯形,,,,,,,分别为,的中点.(1)求证:.(2)若,求二面角的余弦值.中,19.(12分)如图,三棱锥(1)证明:面面;(2)求二面角的余弦值.20.(12分)已知抛物线与直线.(1)求抛物线C上的点到直线l距离的最小值;(2)设点是直线l上的动点,是定点,过点P作抛物线C的两条切线,切点为A,B,求证A,Q,B共线;并在时求点P坐标.21.(12分)已知函数.(1)若函数在上单调递增,求实数的值;(2)定义:若直线与曲线都相切,我们称直线为曲线、的公切线,证明:曲线与总存在公切线.22.(10分)如图,在四棱锥中,底面为矩形,侧面底面,为棱的中点,为棱上任意一点,且不与点、点重合..(1)求证:平面平面;(2)是否存在点使得平面与平面所成的角的余弦值为?若存在,求出点的位置;若不存在,请说明理由.参考答案一、选择题:本题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的。1、C【解析】将圆锥的体积用两种方式表达,即,解出即可.【详解】设圆锥底面圆的半径为r,则,又,故,所以,.故选:C.【点睛】本题利用古代数学问题考查圆锥体积计算的实际应用,考查学生的运算求解能力、创新能力.2、A【解析】试题分析:,,所以,即集合中共有3.故选A.个元素,故选A.考点:集合的运算.3、A【解析】因为,所以排除C、D.当从负方向趋近于0时,,可得4、A【解析】根据向量平行的坐标表示即可求解.【详解...