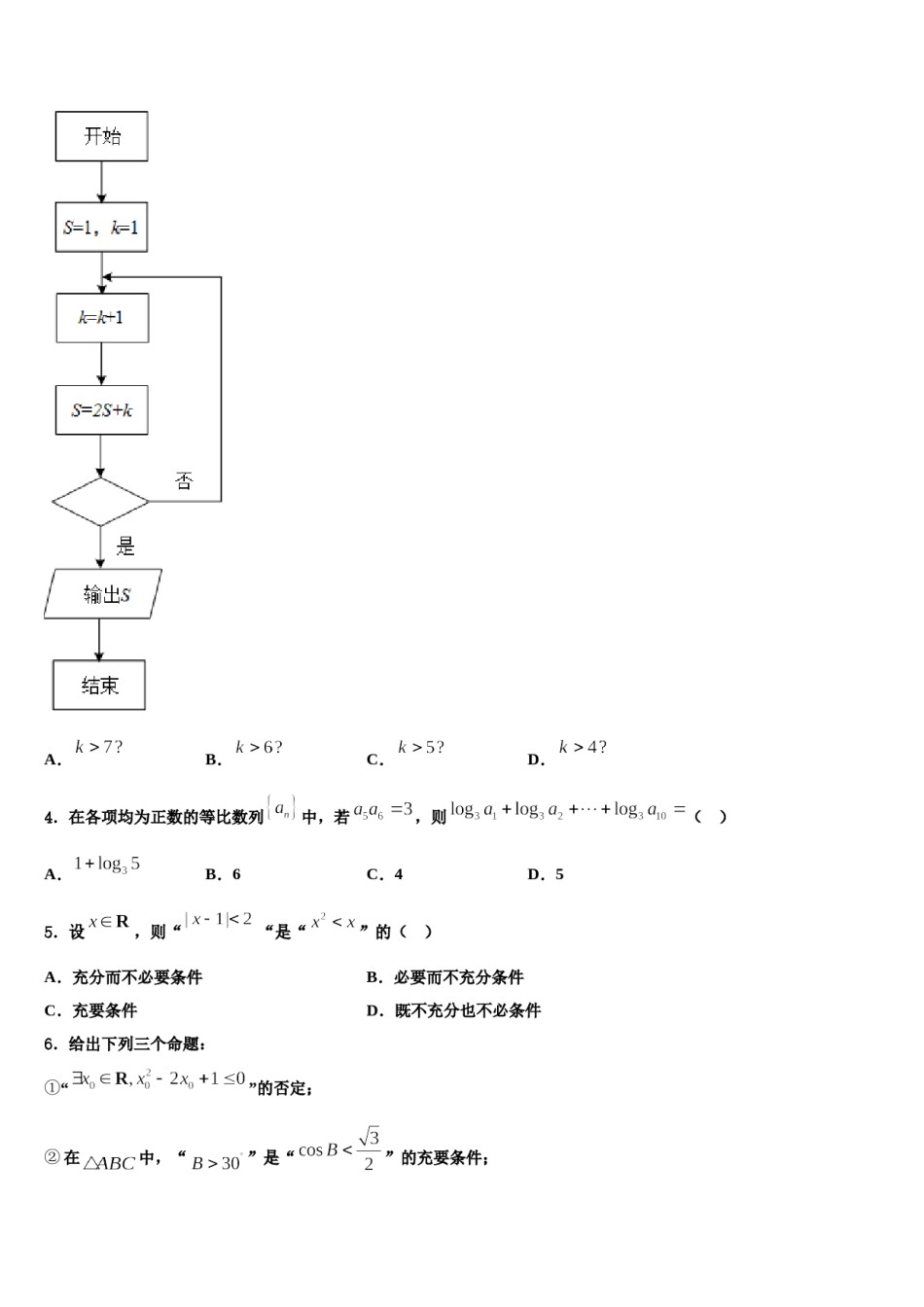
2023-2024学年河南省鹤壁一中高考冲刺模拟数学试题请考生注意:1.请用2B铅笔将选择题答案涂填在答题纸相应位置上,请用0.5毫米及以上黑色字迹的钢笔或签字笔将主观题的答案写在答题纸相应的答题区内。写在试题卷、草稿纸上均无效。2.答题前,认真阅读答题纸上的《注意事项》,按规定答题。一、选择题:本题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的。1.已知双曲线的右焦点为,过的直线交双曲线的渐近线于两点,且直线的倾斜角是渐近线倾斜角的2倍,若,则该双曲线的离心率为()A.B.C.D.2.如图,网格纸上小正方形的边长为1,粗线画出的是某几何体的三视图,则该几何体的表面积()A.B.C.D.3.某程序框图如图所示,若输出的,则判断框内为()A.B.C.D.4.在各项均为正数的等比数列中,若,则()A.B.6C.4D.55.设,则““是“”的()”的否定;A.充分而不必要条件B.必要而不充分条件C.充要条件D.既不充分也不必条件6.给出下列三个命题:①“②在中,“”是“”的充要条件;③将函数的图象向左平移个单位长度,得到函数的图象.其中假命题的个数是()A.0B.1C.2D.37.若双曲线的离心率为,则双曲线的焦距为()A.B.C.6D.88.某部队在一次军演中要先后执行六项不同的任务,要求是:任务A必须排在前三项执行,且执行任务A之后需立即执行任务E,任务B、任务C不能相邻,则不同的执行方案共有()A.36种B.44种C.48种D.54种9.已知直线:与椭圆交于、两点,与圆:交于、两点.若存在,使得,则椭圆的离心率的取值范围为()A.B.C.D.10.把函数图象上各点的横坐标伸长为原来的2倍,纵坐标不变,再将图象向右平移个单位,那么所得图象的一个对称中心为()A.B.C.D.11.设函数(,)是上的奇函数,若的图象关于直线对称,且在区间上是单调函数,则()A.B.C.D.12.一个几何体的三视图如图所示,则该几何体的体积为()A.B.C.D.二、填空题:本题共4小题,每小题5分,共20分。13.已知点M是曲线y=2lnx+x2﹣3x上一动点,当曲线在M处的切线斜率取得最小值时,该切线的方程为_______.14.已知平面向量、的夹角为,且,则的最大值是_____.15.已知(2x-1)7=ao+a1x+a2x2+…+a7x7,则a2=____.16.已知全集为R,集合,则___________.三、解答题:共70分。解答应写出文字说明、证明过程或演算步骤。17.(12分)已知函数,.(1)讨论函数的单调性;(2)已知在处的切线与轴垂直,若方程有三个实数解、、(),求证:.,过的直线与椭圆相交于两点,且与轴相交于点.18.(12分)已知椭圆(1)若,求直线的方程;(2)设关于轴的对称点为,证明:直线过轴上的定点.19.(12分)在数列中,已知,且,.(1)求数列的通项公式;(2)设,数列的前项和为,证明:.,20.(12分)如图,四边形中,,,沿对角线将翻折成,使得.(1)证明:;(2)求直线与平面所成角的正弦值.的首项为0,公差为a,21.(12分)设等差数列;等差数列的首项为0,公差为b,.由数列和构造数表M,与数表;记数表M中位于第i行第j列的元素为,其中,(i,j=1,2,3,…).记数表中位于第i行第j列的元素为,其中(,,).如:,.(1)设,,请计算,,;,试求,的表达式(用i,j表示),并证明:对于整数t,若t不属于数表M,则t属于(2)设,数表;(3)设,,对于整数t,t不属于数表M,求t的最大值.22.(10分)已知为各项均为整数的等差数列,为的前项和,若为和的等比中项,.,求最大的正整数,使得.(1)求数列的通项公式;(2)若参考答案一、选择题:本题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的。1、B【解析】先求出直线l的方程为y(x﹣c),与y=±x联立,可得A,B的纵坐标,利用,求出a,b的关系,即可求出该双曲线的离心率.【详解】双曲线1(a>b>0)的渐近线方程为y=±x, 直线l的倾斜角是渐近线OA倾斜角的2倍,∴kl,∴直线l的方程为y(x﹣c),与y=±x联立,可得y或y, ,∴2•,∴ab,∴c=2b,∴e.故选B.【点睛】本题考查双曲线的简单性质,考查向量知识,考查学生...