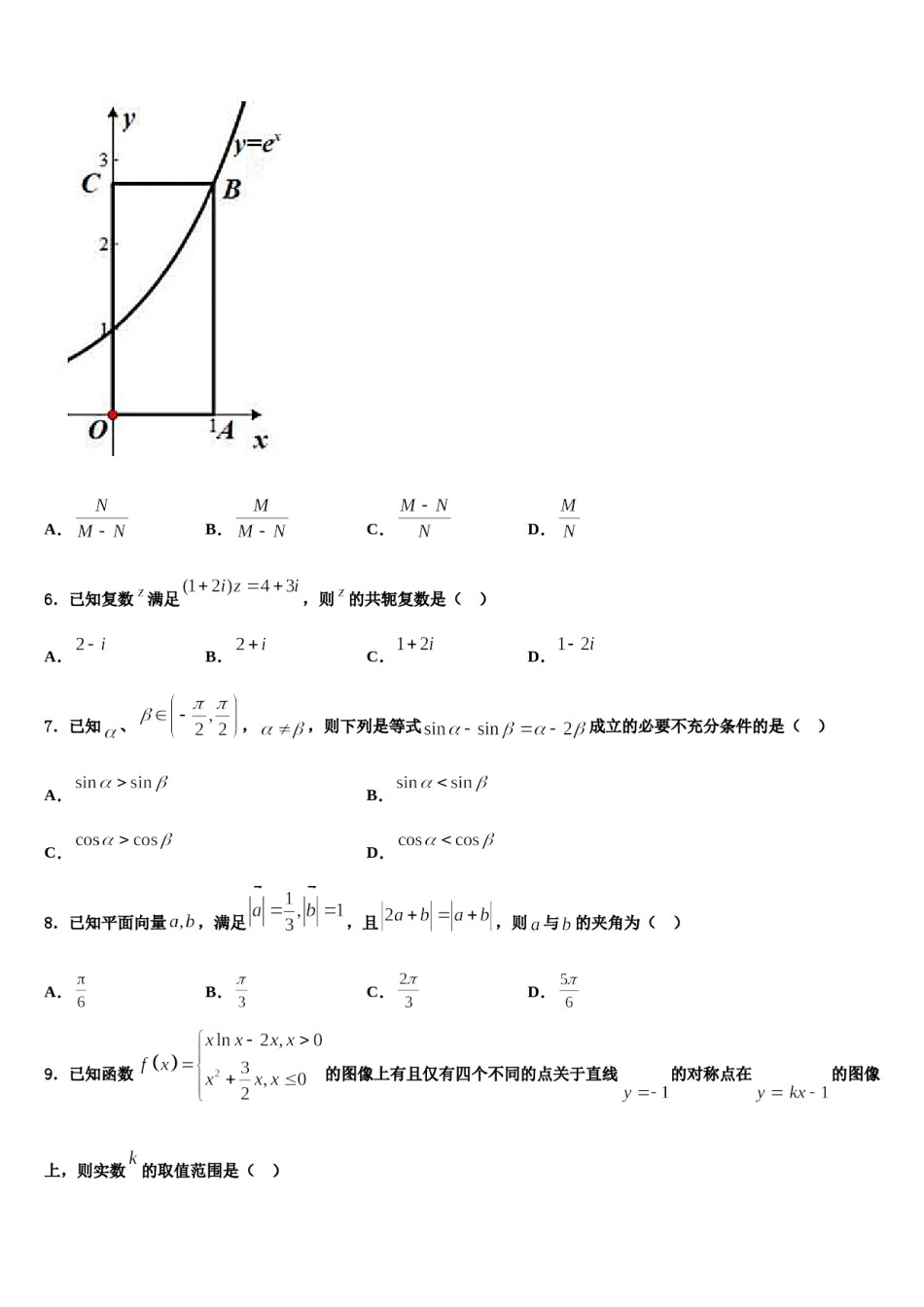
2023-2024学年湖北省枣阳市第一中学高三下学期联考数学试题考生须知:1.全卷分选择题和非选择题两部分,全部在答题纸上作答。选择题必须用2B铅笔填涂;非选择题的答案必须用黑色字迹的钢笔或答字笔写在“答题纸”相应位置上。2.请用黑色字迹的钢笔或答字笔在“答题纸”上先填写姓名和准考证号。3.保持卡面清洁,不要折叠,不要弄破、弄皱,在草稿纸、试题卷上答题无效。一、选择题:本题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的。1.已知函数是奇函数,则的值为()A.-10B.-9C.-7D.1.则此数2.已知数列中,,且当为奇数时,;当为偶数时,列的前项的和为()A.B.C.D.3.各项都是正数的等比数列的公比,且成等差数列,则的值为()A.B.C.D.或4.直线l过抛物线的焦点且与抛物线交于A,B两点,则的最小值是A.10B.9C.8D.75.某人用随机模拟的方法估计无理数的值,做法如下:首先在平面直角坐标系中,过点作轴的垂线与曲线相交于点,过作轴的垂线与轴相交于点(如图),然后向矩形内投入粒豆子,并统计出这些豆子在曲线上方的有粒,则无理数的估计值是()A.B.C.D.6.已知复数满足,则的共轭复数是()A.B.C.D.7.已知、,,则下列是等式成立的必要不充分条件的是()A.B.C.D.8.已知平面向量,满足,且,则与的夹角为()A.B.C.D.9.已知函数的图像上有且仅有四个不同的点关于直线的对称点在的图像上,则实数的取值范围是()A.B.C.D.10.“”是“函数的图象关于直线对称”的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件11.已知实数满足约束条件,则的最小值为()A.-5B.2C.7D.1112.从抛物线为,则直线上一点(点在轴上方)引抛物线准线的垂线,垂足为,且,设抛物线的焦点的斜率为()A.B.C.D.二、填空题:本题共4小题,每小题5分,共20分。13.二项式的展开式中项的系数为_____.14.设函数满足,且当时,又函数,则函数在上的零点个数为___________.15.(5分)已知椭圆方程为,过其下焦点作斜率存在的直线与椭圆交于两点,为坐标原点,则面积的取值范围是____________.16.函数的定义域为______.三、解答题:共70分。解答应写出文字说明、证明过程或演算步骤。17.(12分)已知分别是的内角的对边,且.(Ⅰ)求.(Ⅱ)若,,求的面积.(Ⅲ)在(Ⅱ)的条件下,求的值.18.(12分)选修4-5:不等式选讲已知函数的最大值为3,其中.(1)求的值;(2)若,,,求证:19.(12分)已知函数,且.(1)求的解析式;,若对任意的,总存在,使得成(2)已知立,求的取值范围.的逆矩阵.若曲线:在矩阵A对应的变换作用下得到20.(12分)已知矩阵另一曲线,求曲线的方程.21.(12分)设数列是等差数列,其前项和为,且,.(1)求数列的通项公式;(2)证明:.22.(10分)是数列的前项和,且.(1)求数列的通项公式;(2)若,求数列中最小的项.参考答案一、选择题:本题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的。1、B【解析】根据分段函数表达式,先求得的值,然后结合的奇偶性,求得的值.【详解】因为函数是奇函数,所以,.故选:B【点睛】本题主要考查分段函数的解析式、分段函数求函数值,考查数形结合思想.意在考查学生的运算能力,分析问题、解决问题的能力.2、A【解析】项的奇数项的和,利用等比数列的前项和公式求出前根据分组求和法,利用等差数列的前项和公式求出前项的偶数项的和,进而可求解.【详解】当为奇数时,,则数列奇数项是以为首项,以为公差的等差数列,当为偶数时,,则数列中每个偶数项加是以为首项,以为公比的等比数列.所以.故选:A项和公式、等比数列的前项和公式,需熟记公式,属于基础题.【点睛】本题考查了数列分组求和、等差数列的前3、C【解析】分析:解决该题的关键是求得等比数列的公比,利用题中所给的条件,建立项之间的关系,从而得到公比所满足的等量关系式,解方程即可得结果.详解:根据题意有,即,因为数列各项都是正数,所以,而,故选C.点睛:该题应用题的条件可以求得等...