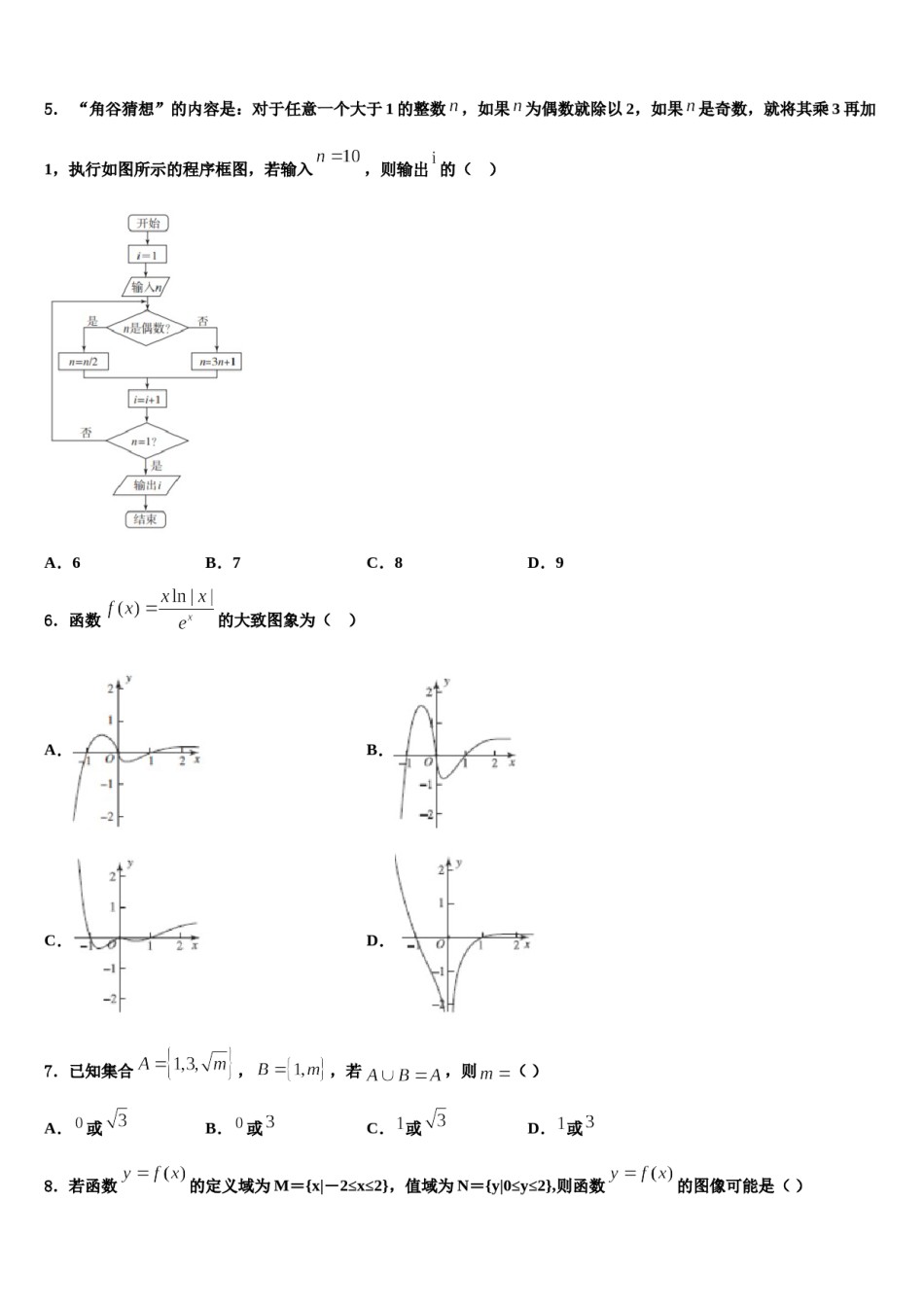
2023-2024学年湖北省黄石市大冶一中高考适应性考试数学试卷注意事项:1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其它答案标号。回答非选择题时,将答案写在答题卡上,写在本试卷上无效。3.考试结束后,将本试卷和答题卡一并交回。一、选择题:本题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的。1.已知正四面体的棱长为,是该正四面体外接球球心,且,,则()A.B.C.D.2.对于定义在上的函数,若下列说法中有且仅有一个是错误的,则错误的一个是()A.在上是减函数B.在上是增函数C.不是函数的最小值D.对于,都有,则”3.下列说法正确的是()A.“若,则”的否命题是“若B.在中,“”是“”成立的必要不充分条件C.“若,则”是真命题D.存在,使得成立4.设递增的等比数列的前n项和为,已知,,则()A.9B.27C.81D.5.“角谷猜想”的内容是:对于任意一个大于1的整数,如果为偶数就除以2,如果是奇数,就将其乘3再加1,执行如图所示的程序框图,若输入,则输出的()A.6B.7C.8D.96.函数的大致图象为()A.B.C.D.7.已知集合,,若,则()A.或8.若函数B.或C.或D.或的定义域为M={x-2≤x≤2},值域为N={y0≤y≤2},则函数的图像可能是()A.B.C.D.9.直线与抛物线C:交于A,B两点,直线,且l与C相切,切点为P,记的面积为S,则A.的最小值为B.C.D.10.已知双曲线C:1(a>0,b>0)的焦距为8,一条渐近线方程为,则C为()A.B.C.D.11.已知双曲线与双曲线有相同的渐近线,则双曲线的离心率为()A.B.C.D.12.已知集合,则A.,集合或C.B.D.二、填空题:本题共4小题,每小题5分,共20分。13.将2个相同的红球和2个相同的黑球全部放入甲、乙、丙、丁四个盒子里,其中甲、乙盒子均最多可放入2个球,丙、丁盒子均最多可放入1个球,且不同颜色的球不能放入同一个盒子里,共有________种不同的放法.14.若复数满足,其中为虚数单位,则的共轭复数在复平面内对应点的坐标为_____.15.已知双曲线(a>0,b>0)的一条渐近线方程为,则该双曲线的离心率为_______.16.如图,在梯形中,∥,分别是的中点,若,则的值为___________.三、解答题:共70分。解答应写出文字说明、证明过程或演算步骤。17.(12分)如图,正方形是某城市的一个区域的示意图,阴影部分为街道,各相邻的两红绿灯之间的距离相等,处为红绿灯路口,红绿灯统一设置如下:先直行绿灯30秒,再左转绿灯30秒,然后是红灯1分钟,右转不受红绿灯影响,这样独立的循环运行.小明上学需沿街道从处骑行到处(不考虑处的红绿灯),出发时的两条路线()等可能选择,且总是走最近路线.(1)请问小明上学的路线有多少种不同可能?(2)在保证通过红绿灯路口用时最短的前提下,小明优先直行,求小明骑行途中恰好经过处,且全程不等红绿灯的概率;(3)请你根据每条可能的路线中等红绿灯的次数的均值,为小明设计一条最佳的上学路线,且应尽量避开哪条路线?18.(12分)△的内角的对边分别为,且.(1)求角的大小(2)若,△的面积,求△的周长.19.(12分)如图,在中,,的角平分线与交于点,.(Ⅰ)求;(Ⅱ)求的面积.20.(12分)已知函数.(Ⅰ)求函数的极值;(Ⅱ)若,且,求证:.21.(12分)如图,三棱柱的侧棱垂直于底面,且,,,,是棱的中点.(1)证明:;(2)求二面角的余弦值.22.(10分)在中,,,.求边上的高.①,②,③,这三个条件中任选一个,补充在上面问题中并作答.参考答案一、选择题:本题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的。1、A【解析】如图设平面,球心在上,根据正四面体的性质可得,根据平面向量的加法的几何意义,重心的性质,结合已知求出的值.上,由正四面体的性质可得:三角形【详解】如图设平面,球心在是正三角形,,,在直角三角形中,,,,,,因为为重心,因此,则,因此,因此,则,故选A.【点睛】本题考查了正四面体的性质,...