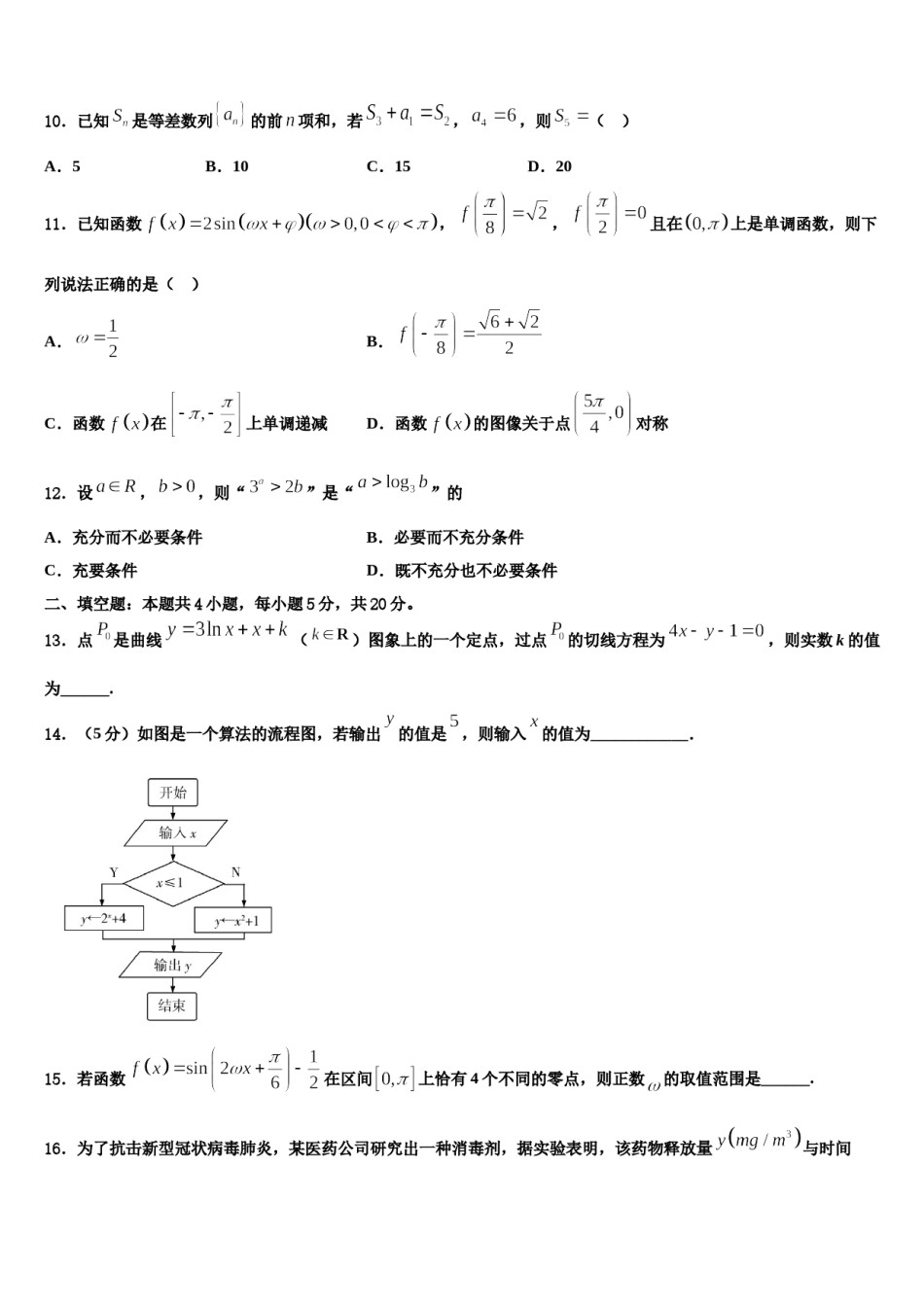
2023-2024学年福建省泉州市永春县第一中学高考仿真模拟数学试卷注意事项1.考试结束后,请将本试卷和答题卡一并交回.2.答题前,请务必将自己的姓名、准考证号用0.5毫米黑色墨水的签字笔填写在试卷及答题卡的规定位置.3.请认真核对监考员在答题卡上所粘贴的条形码上的姓名、准考证号与本人是否相符.4.作答选择题,必须用2B铅笔将答题卡上对应选项的方框涂满、涂黑;如需改动,请用橡皮擦干净后,再选涂其他答案.作答非选择题,必须用05毫米黑色墨水的签字笔在答题卡上的指定位置作答,在其他位置作答一律无效.5.如需作图,须用2B铅笔绘、写清楚,线条、符号等须加黑、加粗.一、选择题:本题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的。1.已知椭圆(a>b>0)与双曲线(a>0,b>0)的焦点相同,则双曲线渐近线方程为()A.B.C.D.2.设a,b,c为正数,则“”是“”的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不修要条件3.著名的斐波那契数列:1,1,2,3,5,8,…,满足,,,若,则()A.2020B.4038C.4039D.40404.函数的图象可能是下列哪一个?()A.B.C.D.5.设为抛物线的焦点,,,为抛物线上三点,若,则().A.9B.6C.D.6.已知复数满足,则()A.B.2C.4D.37.函数的最大值为,最小正周期为,则有序数对为()A.B.C.D.8.i是虚数单位,若,则乘积的值是()A.-15B.-3C.3D.15时该命题成立,则9.某个命题与自然数有关,且已证得“假设时该命题也成立”.现已知当时,该命题不成立,那么()A.当时,该命题不成立B.当时,该命题成立D.当时,该命题成立C.当时,该命题不成立10.已知是等差数列的前项和,若,,则()D.20A.5B.10C.1511.已知函数,,且在上是单调函数,则下列说法正确的是()A.B.C.函数在上单调递减D.函数的图像关于点对称12.设,,则“”是“”的A.充分而不必要条件B.必要而不充分条件C.充要条件D.既不充分也不必要条件二、填空题:本题共4小题,每小题5分,共20分。13.点是曲线()图象上的一个定点,过点的切线方程为,则实数k的值为______.14.(5分)如图是一个算法的流程图,若输出的值是,则输入的值为____________.15.若函数在区间上恰有4个不同的零点,则正数的取值范围是______.16.为了抗击新型冠状病毒肺炎,某医药公司研究出一种消毒剂,据实验表明,该药物释放量与时间的函数关系为(如图所示),实验表明,当药物释放量对人体无害.(1)______;(2)为了不使人身体受到药物伤害,若使用该消毒剂对房间进行消毒,则在消毒后至少经过______分钟人方可进入房间.三、解答题:共70分。解答应写出文字说明、证明过程或演算步骤。,(其中)17.(12分)已知.(1)求;(2)求证:当时,.18.(12分)已知椭圆的上顶点为,圆与轴的正半轴交于点,与有且仅有两个交点且都在轴上,(为坐标原点).(1)求椭圆的方程;(2)已知点,不过点且斜率为的直线与椭圆交于两点,证明:直线与直线的斜率互为相反数.19.(12分)已知分别是椭圆的左、右焦点,直线与交于两点,,且.(1)求的方程;两点,直线的斜率都存(2)已知点是上的任意一点,不经过原点的直线与交于在,且,求的值.20.(12分)已知,均为给定的大于1的自然数,设集合,.(Ⅰ)当,时,用列举法表示集合;(Ⅱ)当时,,且集合满足下列条件:①对任意,;②.证明:(ⅰ)若,则(集合为集合在集合中的补集);(ⅱ)为一个定值(不必求出此定值);(Ⅲ)设,,,其中,,若,则.21.(12分)已知椭圆的离心率为,点在椭圆上.上,求证:线段的中垂线恒过定(Ⅰ)求椭圆的标准方程;(Ⅱ)设直线交椭圆于两点,线段的中点在直线点.22.(10分)已知矩阵,.求矩阵;求矩阵的特征值.参考答案一、选择题:本题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的。1、A【解析】由题意可得,即,代入双曲线的渐近线方程可得答案.【详解】依题意椭圆与双曲线即的焦点相同,可得:,即,∴,可得,双曲线的渐近线方程为:,故选:A.【点...