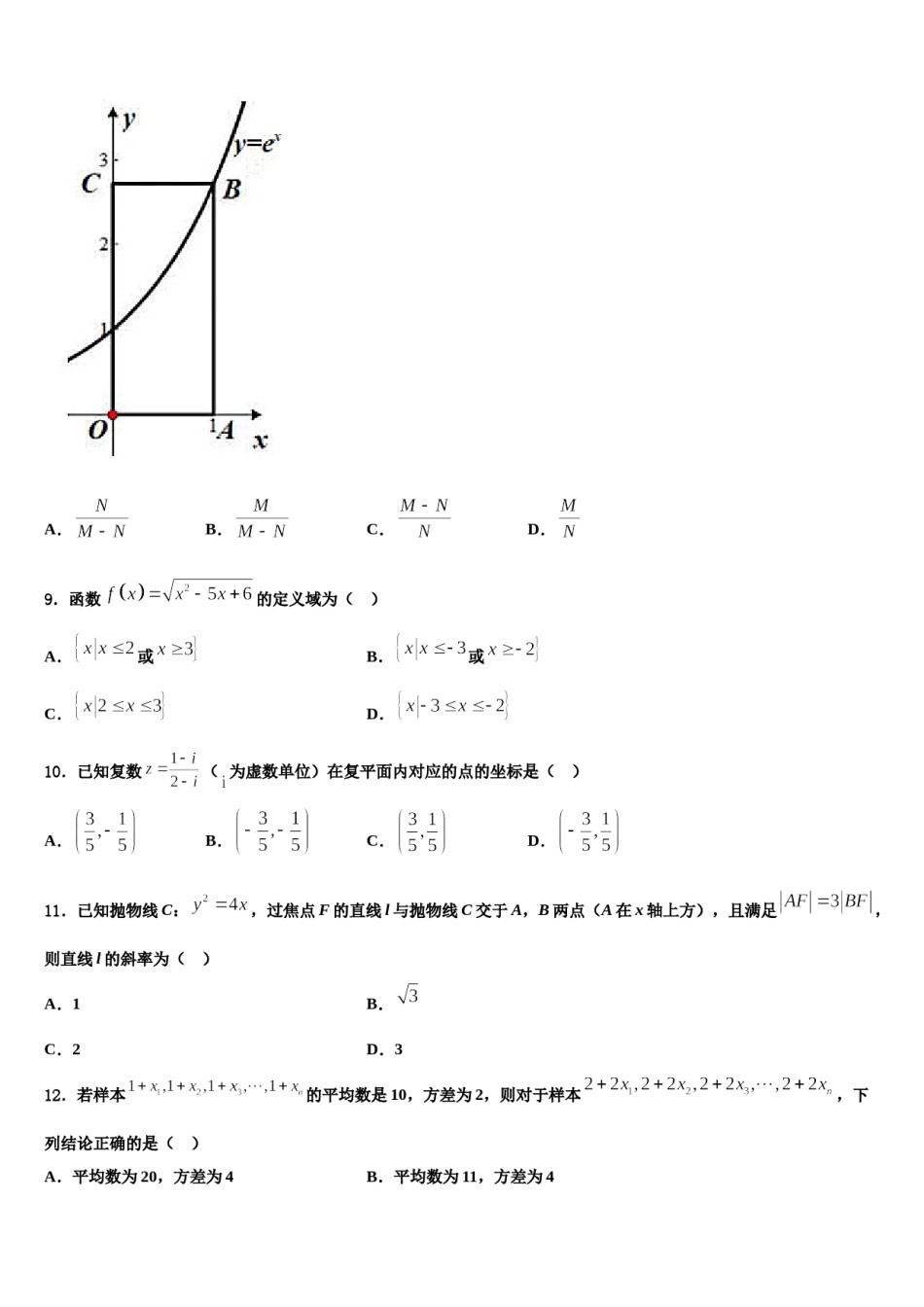
2023-2024学年辽宁省大连市普兰店区第二中学高三第四次模拟考试数学试卷考生请注意:1.答题前请将考场、试室号、座位号、考生号、姓名写在试卷密封线内,不得在试卷上作任何标记。2.第一部分选择题每小题选出答案后,需将答案写在试卷指定的括号内,第二部分非选择题答案写在试卷题目指定的位置上。3.考生必须保证答题卡的整洁。考试结束后,请将本试卷和答题卡一并交回。一、选择题:本题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的。1.已知向量,,,若,则()A.B.C.D.2.已知等差数列的公差不为零,且,,构成新的等差数列,为的前项和,若存在使得,则()A.10B.11C.12D.13,,则直线与3.直三棱柱中,所成的角的余弦值为()C.A.B.D.4.已知的内角、、的对边分别为、、,且,,为边上的中线,若,则的面积为()A.B.C.D.5.已知复数满足,则的最大值为()A.B.C.D.66.若向量,,则与共线的向量可以是()A.B.C.D.7.如图是计算值的一个程序框图,其中判断框内应填入的条件是()A.作轴的垂线与曲B.C.D.8.某人用随机模拟的方法估计无理数的值,做法如下:首先在平面直角坐标系中,过点线相交于点,过作轴的垂线与轴相交于点(如图),然后向矩形内投入粒豆子,并统计出这些豆子在曲线上方的有粒,则无理数的估计值是()A.B.C.D.9.函数的定义域为()A.或B.或C.D.10.已知复数(为虚数单位)在复平面内对应的点的坐标是()A.B.C.D.11.已知抛物线C:,过焦点F的直线l与抛物线C交于A,B两点(A在x轴上方),且满足,,下则直线l的斜率为()A.1B.C.2D.312.若样本的平均数是10,方差为2,则对于样本列结论正确的是()B.平均数为11,方差为4A.平均数为20,方差为4C.平均数为21,方差为8D.平均数为20,方差为8二、填空题:本题共4小题,每小题5分,共20分。13.曲线在点处的切线方程为________.14.锐角中,角,,所对的边分别为,,,若,则的取值范围是______.15.在平面直角坐标系中,双曲线的焦距为,若过右焦点且与轴垂直的直线与两条渐近线围成的三角形面积为,则双曲线的离心率为____________.16.的展开式中的系数为__________.三、解答题:共70分。解答应写出文字说明、证明过程或演算步骤。17.(12分)已知椭圆过点,设椭圆的上顶点为,右顶点和右焦点分别为,,且.(1)求椭圆的标准方程;(2)设直线交椭圆于,两点,设直线与直线的斜率分别为,,若,试判断直线是否过定点?若过定点,求出该定点的坐标;若不过定点,请说明理由.18.(12分)在平面直角坐标系xOy中,椭圆C:的右准线方程为x=2,且两焦点与短轴的一个顶点构成等腰直角三角形.(1)求椭圆C的方程;(2)假设直线l:与椭圆C交于A,B两点.①若A为椭圆的上顶点,M为线段AB中点,连接OM并延长交椭圆C于N,并且,求OB的长;②若原点O到直线l的距离为1,并且,当时,求△OAB的面积S的范围.19.(12分)若正数满足,求的最小值.20.(12分)已知中心在原点的椭圆的左焦点为,与轴正半轴交点为,且.时,直线(1)求椭圆的标准方程;(2)过点作斜率为、的两条直线分别交于异于点的两点、.证明:当过定点.21.(12分)在三角形ABC中,角A,B,C的对边分别为a,b,c,若,角为钝角,(1)求的值;(2)求边的长.22.(10分)如图,已知四边形的直角梯形,∥BC,,,,为线段的中点,平面,,为线段上一点(不与端点重合).(1)若,(ⅰ)求证:PC∥平面;(ⅱ)求平面与平面所成的锐二面角的余弦值;(2)否存在实数满足,使得直线与平面所成的角的正弦值为,若存在,确定的值,若不存在,请说明理由.参考答案一、选择题:本题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的。1、A【解析】根据向量坐标运算求得,由平行关系构造方程可求得结果.【详解】,,解得:故选:【点睛】本题考查根据向量平行关系求解参数值的问题,涉及到平面向量的坐标运算;关键是明确若两向量平行,则.,再利用等差数列的前项和公式即可求解.2、D【解析】利用等差数列的通项公式可得【详...