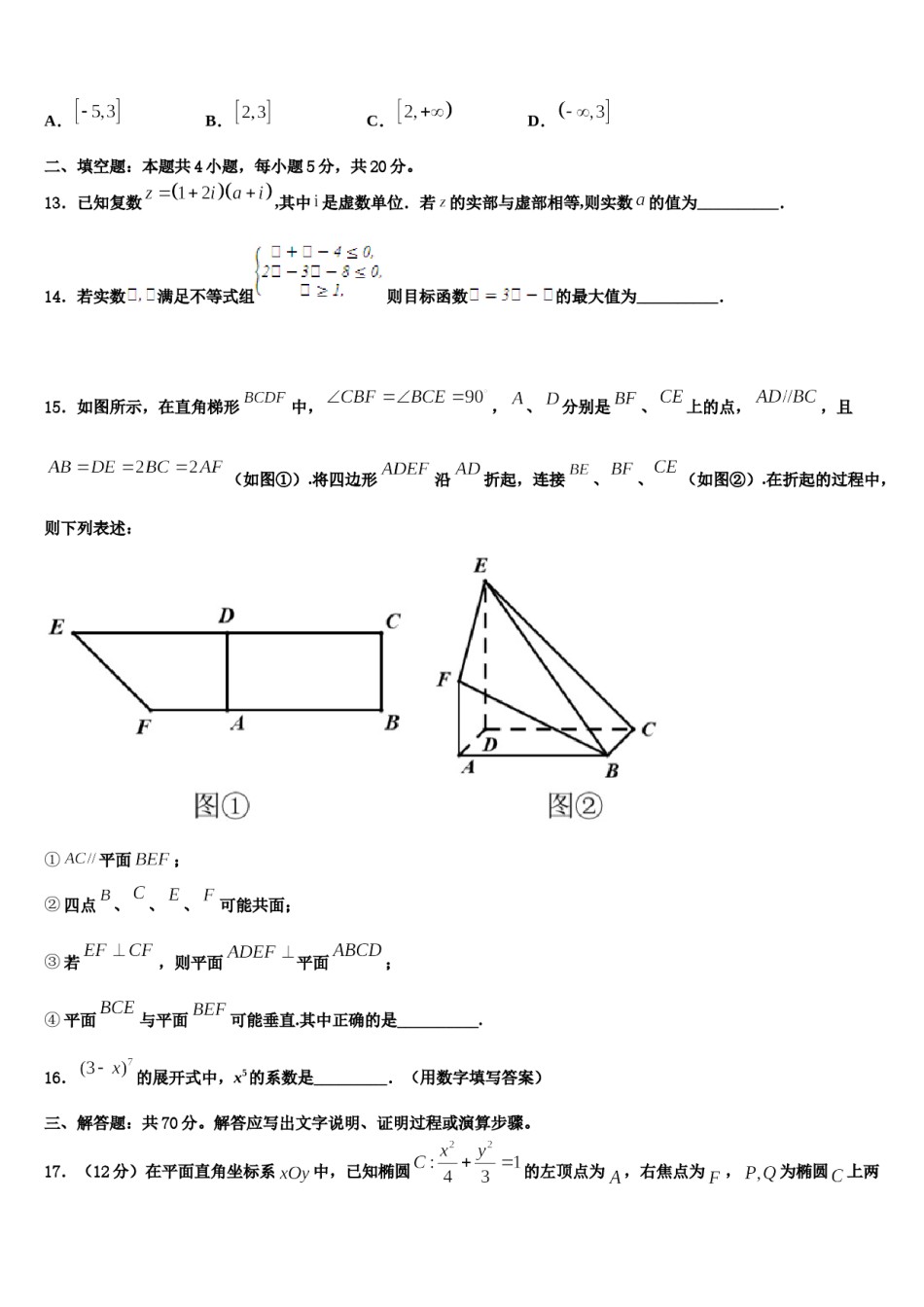
2023-2024学年重庆市綦江区南州中学高考仿真卷数学试卷请考生注意:1.请用2B铅笔将选择题答案涂填在答题纸相应位置上,请用0.5毫米及以上黑色字迹的钢笔或签字笔将主观题的答案写在答题纸相应的答题区内。写在试题卷、草稿纸上均无效。2.答题前,认真阅读答题纸上的《注意事项》,按规定答题。一、选择题:本题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的。1.某地区高考改革,实行“3+2+1”模式,即“3”指语文、数学、外语三门必考科目,“1”指在物理、历史两门科目中必选一门,“2”指在化学、生物、政治、地理以及除了必选一门以外的历史或物理这五门学科中任意选择两门学科,则一名学生的不同选科组合有()A.8种B.12种C.16种D.20种2.已知函数,则()A.函数在上单调递增B.函数在上单调递减C.函数图像关于对称D.函数图像关于对称3.已知排球发球考试规则:每位考生最多可发球三次,若发球成功,则停止发球,否则一直发到次结束为止.某考生一次发球成功的概率为,发球次数为,若的数学期望,则的取值范围为()A.B.C.D.4.大衍数列,米源于我国古代文献《乾坤谱》中对易传“大衍之数五十”的推论,主要用于解释我国传统文化中的太极衍生原理,数列中的每一项,都代表太极衍生过程中,曾经经历过的两仪数量总和.已知该数列前10项是0,2,4,8,12,18,24,32,40,50,…,则大衍数列中奇数项的通项公式为()A.B.C.D.5.已知抛物线:,直线与分别相交于点,与的准线相交于点,若,则()A.3B.C.D.6.过直线上一点作圆的两条切线,,,为切点,当直线,关于直线对称时,()A.B.C.D.7.小王因上班繁忙,来不及做午饭,所以叫了外卖.假设小王和外卖小哥都在12:00~12:10之间随机到达小王所居住的楼下,则小王在楼下等候外卖小哥的时间不超过5分钟的概率是()A.B.C.D.8.已知集合,则集合的非空子集个数是()A.2B.3C.7D.89.2020年是脱贫攻坚决战决胜之年,某市为早日实现目标,现将甲、乙、丙、丁4名干部派遺到、、三个贫困县扶贫,要求每个贫困县至少分到一人,则甲被派遣到县的分法有()A.6种B.12种C.24种D.36种10.若复数满足,其中为虚数单位,是的共轭复数,则复数()A.B.C.4D.511.在中,角的对边分别为,,若,,且,则的面积为()A.B.C.D.12.设,满足,则的取值范围是()A.B.C.D.二、填空题:本题共4小题,每小题5分,共20分。13.已知复数,其中是虚数单位.若的实部与虚部相等,则实数的值为__________.14.若实数满足不等式组则目标函数的最大值为__________.15.如图所示,在直角梯形中,,、分别是、上的点,,且(如图①).将四边形沿折起,连接、、(如图②).在折起的过程中,则下列表述:①平面;②四点、、、可能共面;③若,则平面平面;④平面与平面可能垂直.其中正确的是__________.16.的展开式中,x5的系数是_________.(用数字填写答案)三、解答题:共70分。解答应写出文字说明、证明过程或演算步骤。17.(12分)在平面直角坐标系中,已知椭圆的左顶点为,右焦点为,为椭圆上两点,圆.(1)若轴,且满足直线与圆相切,求圆的方程;(2)若圆的半径为,点满足,求直线被圆截得弦长的最大值.18.(12分)在直角坐标系中,已知直线的直角坐标方程为,曲线的参数方程为(为参数),以直角坐标系原点为极点,轴的正半轴为极轴建立极坐标系,曲线的极坐标方程为.(1)求曲线和直线的极坐标方程;(2)已知直线与曲线、相交于异于极点的点,若的极径分别为,求的值.19.(12分)如图,在四棱锥中,底面是菱形,∠,是边长为2的正三角形,,为线段的中点.(1)求证:平面平面;(2)若为线段上一点,当二面角的余弦值为时,求三棱锥的体积.20.(12分)如图,已知椭圆,为其右焦点,直线与椭圆交于两点,点在上,且满足.(点从上到下依次排列)(I)试用表示:(II)证明:原点到直线l的距离为定值.21.(12分)已知数列的各项均为正数,且满足.,以坐标原点O为极点,x轴的正半轴为极轴建(1)求,及的通项公式;(2)求数列的前项和.22.(10分)在平面直...