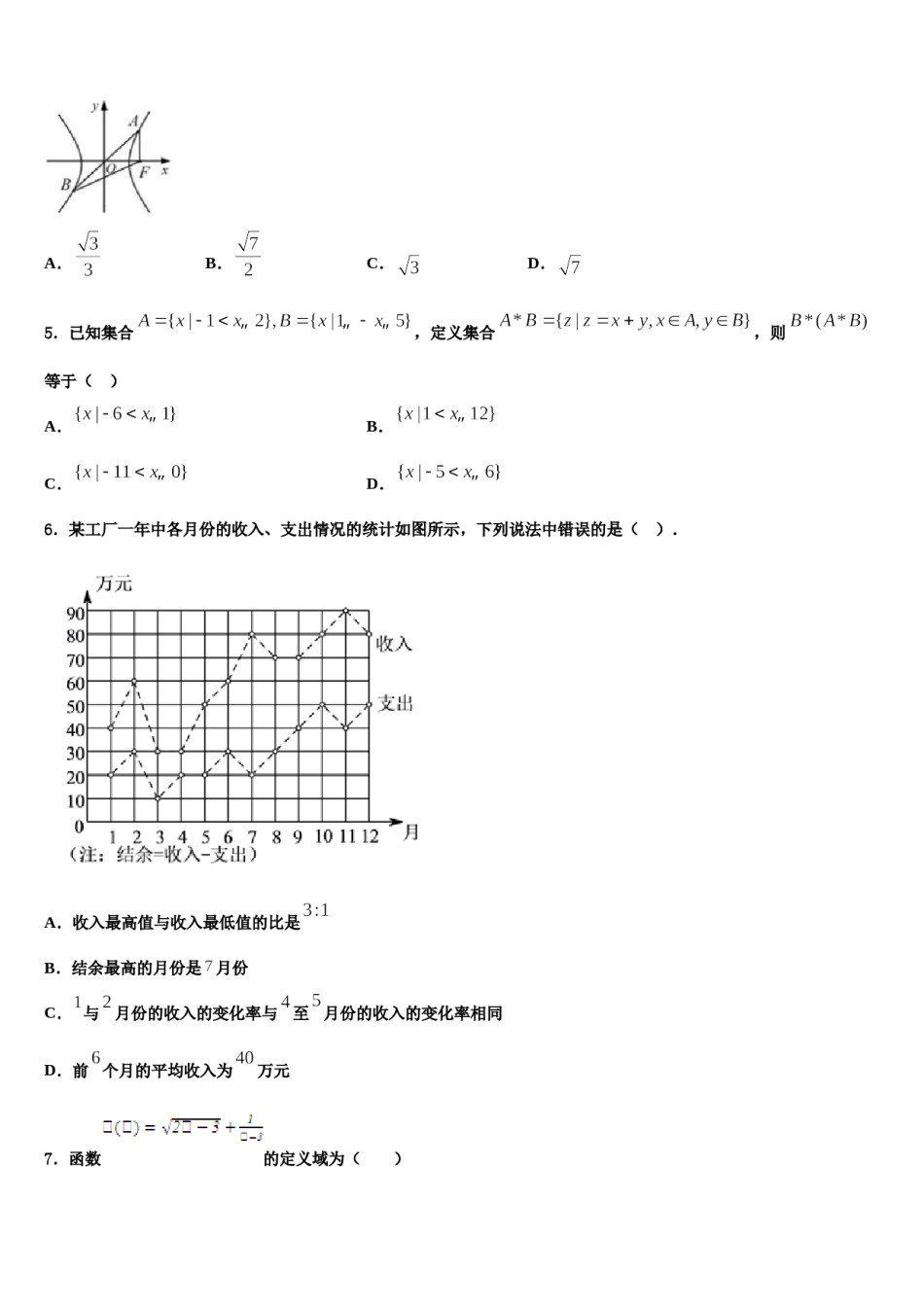
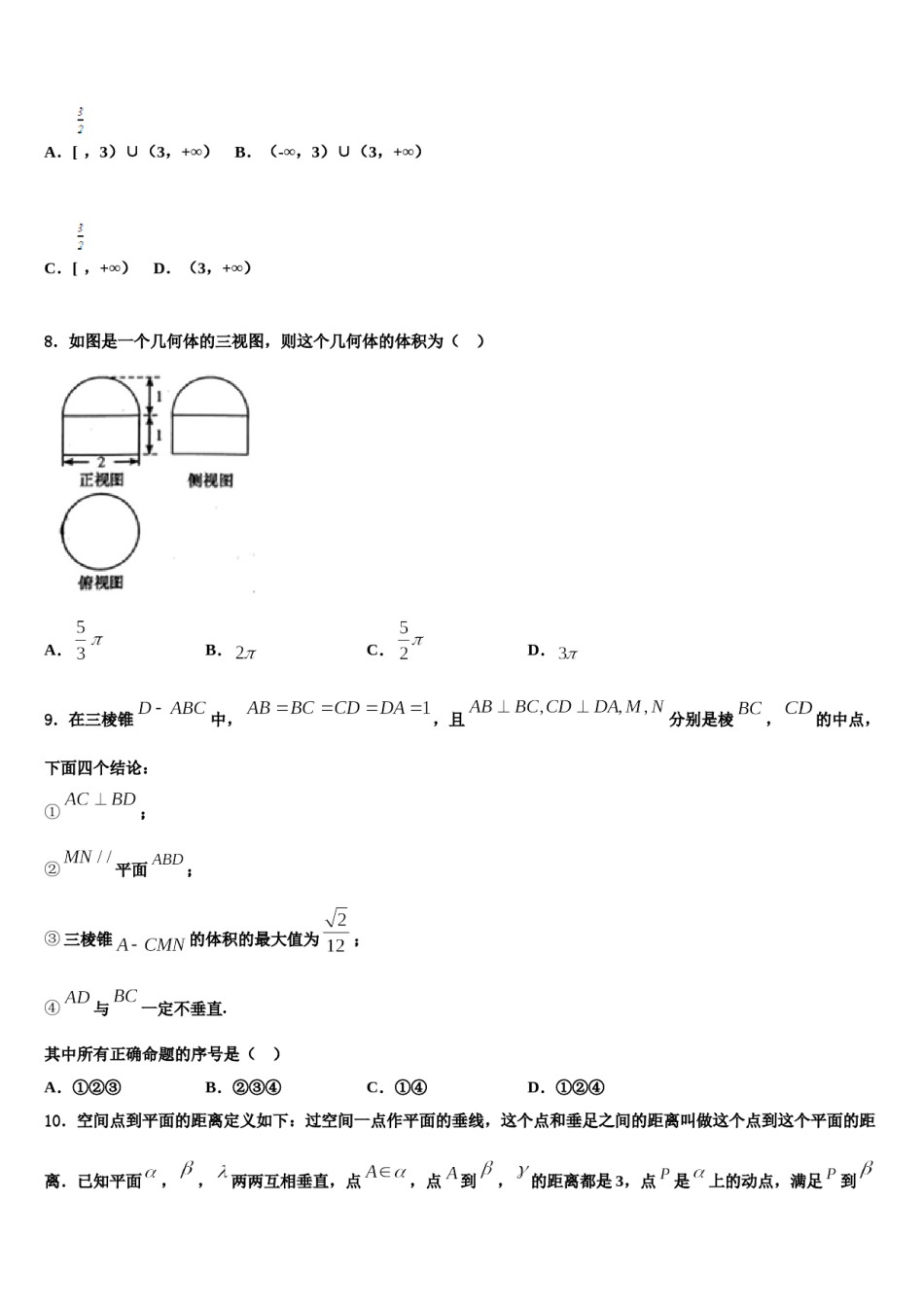
2023-2024学年黑龙江省泰来县第一中学高三第三次测评数学试卷注意事项:1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其它答案标号。回答非选择题时,将答案写在答题卡上,写在本试卷上无效。3.考试结束后,将本试卷和答题卡一并交回。一、选择题:本题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的。1.我们熟悉的卡通形象“哆啦A梦”的长宽比为.在东方文化中通常称这个比例为“白银比例”,该比例在设计和建筑领域有着广泛的应用.已知某电波塔自下而上依次建有第一展望台和第二展望台,塔顶到塔底的高度与第二展望台到塔底的高度之比,第二展望台到塔底的高度与第一展望台到塔底的高度之比皆等于“白银比例”,若两展望台间高度差为100米,则下列选项中与该塔的实际高度最接近的是()A.400米B.480米C.520米D.600米2.“哥德巴赫猜想”是近代三大数学难题之一,其内容是:一个大于2的偶数都可以写成两个质数(素数)之和,也就是我们所谓的“1+1”问题.它是1742年由数学家哥德巴赫提出的,我国数学家潘承洞、王元、陈景润等在哥德巴赫猜想的证明中做出相当好的成绩.若将6拆成两个正整数的和,则拆成的和式中,加数全部为质数的概率为()A.B.C.D.3.如图是二次函数的部分图象,则函数的零点所在的区间是()A.B.C.D.4.如图所示,已知双曲线的右焦点为,双曲线的右支上一点,它关于原点的对称点为,满足,且,则双曲线的离心率是().A.B.C.D.5.已知集合,定义集合,则等于()B.A.C.D.6.某工厂一年中各月份的收入、支出情况的统计如图所示,下列说法中错误的是().A.收入最高值与收入最低值的比是B.结余最高的月份是月份C.与月份的收入的变化率与至月份的收入的变化率相同D.前个月的平均收入为万元7.函数的定义域为()A.[,3)∪(3,+∞)B.(-∞,3)∪(3,+∞)C.[,+∞)D.(3,+∞)8.如图是一个几何体的三视图,则这个几何体的体积为()A.B.C.D.9.在三棱锥中,,且分别是棱,的中点,下面四个结论:①;②平面;③三棱锥的体积的最大值为;④与一定不垂直.其中所有正确命题的序号是()A.①②③B.②③④C.①④D.①②④10.空间点到平面的距离定义如下:过空间一点作平面的垂线,这个点和垂足之间的距离叫做这个点到这个平面的距离.已知平面,,两两互相垂直,点,点到,的距离都是3,点是上的动点,满足到的距离与到点的距离相等,则点的轨迹上的点到的距离的最小值是()A.B.3C.D.11.已知复数在复平面内对应的点的坐标为,则下列结论正确的是()A.B.复数的共轭复数是C.D.12.设,则()A.B.C.D.二、填空题:本题共4小题,每小题5分,共20分。13.若,则的最小值是______.14.运行下面的算法伪代码,输出的结果为_____.15.数列的前项和为,数列的前项和为,满足,,且.若任意,成立,则实数的取值范围为__________.16.直线是圆:与圆:的公切线,并且分别与轴正半轴,轴正半轴相交于,两点,则的面积为_________三、解答题:共70分。解答应写出文字说明、证明过程或演算步骤。17.(12分)如图,在三棱柱中,平面平面,侧面为平行四边形,侧面为正方形,,,为的中点.(1)求证:平面;(2)求二面角的大小.18.(12分)已知等差数列中,,数列的前项和.(1)求;(2)若,求的前项和.19.(12分)如图,在四棱锥PABCD中,PA⊥平面ABCD,∠ABC=∠BAD=90°,AD=AP=4,AB=BC=2,M为PC的中点.(1)求异面直线AP,BM所成角的余弦值;>1,(2)点N在线段AD上,且AN=λ,若直线MN与平面PBC所成角的正弦值为,求λ的值.20.(12分)已知函数f(x)=x-lnx,g(x)=x2-ax.(1)求函数f(x)在区间[t,t+1](t>0)上的最小值m(t);(2)令h(x)=g(x)-f(x),A(x1,h(x1)),B(x2,h(x2))(x1≠x2)是函数h(x)图像上任意两点,且满足求实数a的取值范围;(3)若∃x∈(0,1],使f(x)≥成立,求实数a的最大值.21.(12分)设函数.(Ⅰ)讨论函...