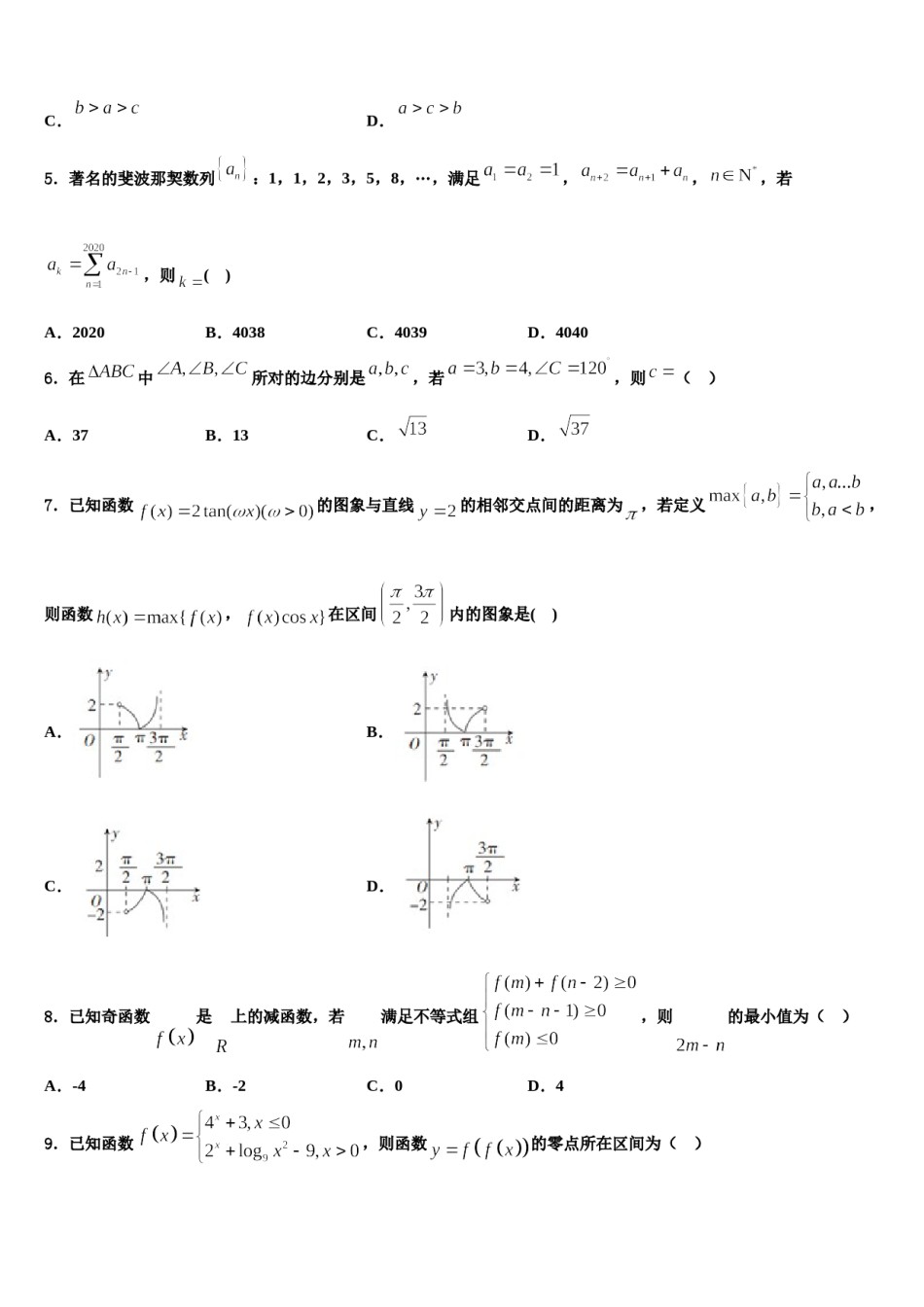
2024届上海市浦东新区建平中学高三(最后冲刺)数学试卷注意事项:1.答卷前,考生务必将自己的姓名、准考证号、考场号和座位号填写在试题卷和答题卡上。用2B铅笔将试卷类型(B)填涂在答题卡相应位置上。将条形码粘贴在答题卡右上角"条形码粘贴处"。2.作答选择题时,选出每小题答案后,用2B铅笔把答题卡上对应题目选项的答案信息点涂黑;如需改动,用橡皮擦干净后,再选涂其他答案。答案不能答在试题卷上。3.非选择题必须用黑色字迹的钢笔或签字笔作答,答案必须写在答题卡各题目指定区域内相应位置上;如需改动,先划掉原来的答案,然后再写上新答案;不准使用铅笔和涂改液。不按以上要求作答无效。4.考生必须保证答题卡的整洁。考试结束后,请将本试卷和答题卡一并交回。一、选择题:本题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的。1.设是两条不同的直线,是两个不同的平面,则下列命题正确的是()A.若,,则B.若,,则C.若,,,则D.若,,,则2.是边长为的等边三角形,、分别为、的中点,沿把折起,使点翻折到点的位置,连接、,当四棱锥的外接球的表面积最小时,四棱锥的体积为()A.B.C.D.3.如图,四边形为平行四边形,为中点,为的三等分点(靠近)若,则的值为()A.B.C.D.4.若,,,则()A.B.C.D.5.著名的斐波那契数列:1,1,2,3,5,8,…,满足,,,若,则()A.2020B.4038C.4039D.4040,则6.在中所对的边分别是,若()A.37B.13C.D.7.已知函数的图象与直线的相邻交点间的距离为,若定义,则函数,在区间内的图象是()A.B.C.D.8.已知奇函数是上的减函数,若满足不等式组,则的最小值为()A.-4B.-2C.0D.49.已知函数,则函数的零点所在区间为()A.B.C.D.10.已知中,角、所对的边分别是,,则“”是“”的()A.充分不必要条件B.必要不充分条件C.既不充分也不必要条件D.充分必要条件11.已知集合,则()A.B.C.D.12.设全集U=R,集合,则()A.{x-1<x<4}B.{x-4<x<1}C.{x-1≤x≤4}D.{x-4≤x≤1}二、填空题:本题共4小题,每小题5分,共20分。13.三所学校举行高三联考,三所学校参加联考的人数分别为160,240,400,为调查联考数学学科的成绩,现采用分层抽样的方法在这三所学校中抽取样本,若在学校抽取的数学成绩的份数为30,则抽取的样本容量为____________.14.已知,若,则a的取值范围是______.15.甲、乙、丙、丁四人参加冬季滑雪比赛,有两人获奖.在比赛结果揭晓之前,四人的猜测如下表,其中“√”表示猜测某人获奖,“×”表示猜测某人未获奖,而“○”则表示对某人是否获奖未发表意见.已知四个人中有且只有两个人的猜测是正确的,那么两名获奖者是_______.甲获奖乙获奖丙获奖丁获奖甲的猜测√××√乙的猜测×○○√丙的猜测×√×√丁的猜测○○√×16.若函数为偶函数,则.三、解答题:共70分。解答应写出文字说明、证明过程或演算步骤。17.(12分)如图,在四棱锥中,底面为等腰梯形,,为等腰直角三角形,,平面底面,为的中点.(1)求证:平面;(2)若平面与平面的交线为,求二面角的正弦值.,18.(12分)如图,在直三棱柱中,,为的中点,点在线段上,且平面.(1)求证:;(2)求平面与平面所成二面角的正弦值.19.(12分)设函数.(1)当时,求不等式的解集;(2)若不等式恒成立,求实数a的取值范围.20.(12分)已知.(1)若是上的增函数,求的取值范围;(2)若函数有两个极值点,判断函数零点的个数.21.(12分)已知,分别是椭圆:的左,右焦点,点在椭圆上,且抛物线的焦点是椭圆的一个焦点.(1)求,的值:(2)过点作不与轴重合的直线,设与圆相交于A,B两点,且与椭圆相交于C,D两点,当时,求△的面积.22.(10分)已知数列和满足,,,,.,若对,恒成立,求正整数的值.(Ⅰ)求与;(Ⅱ)记数列的前项和为,且参考答案一、选择题:本题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的。1、C【解析】根据空间中直线与平面、平面与平面位置关系相关定理依次判断各个选项可得结果.【详解...