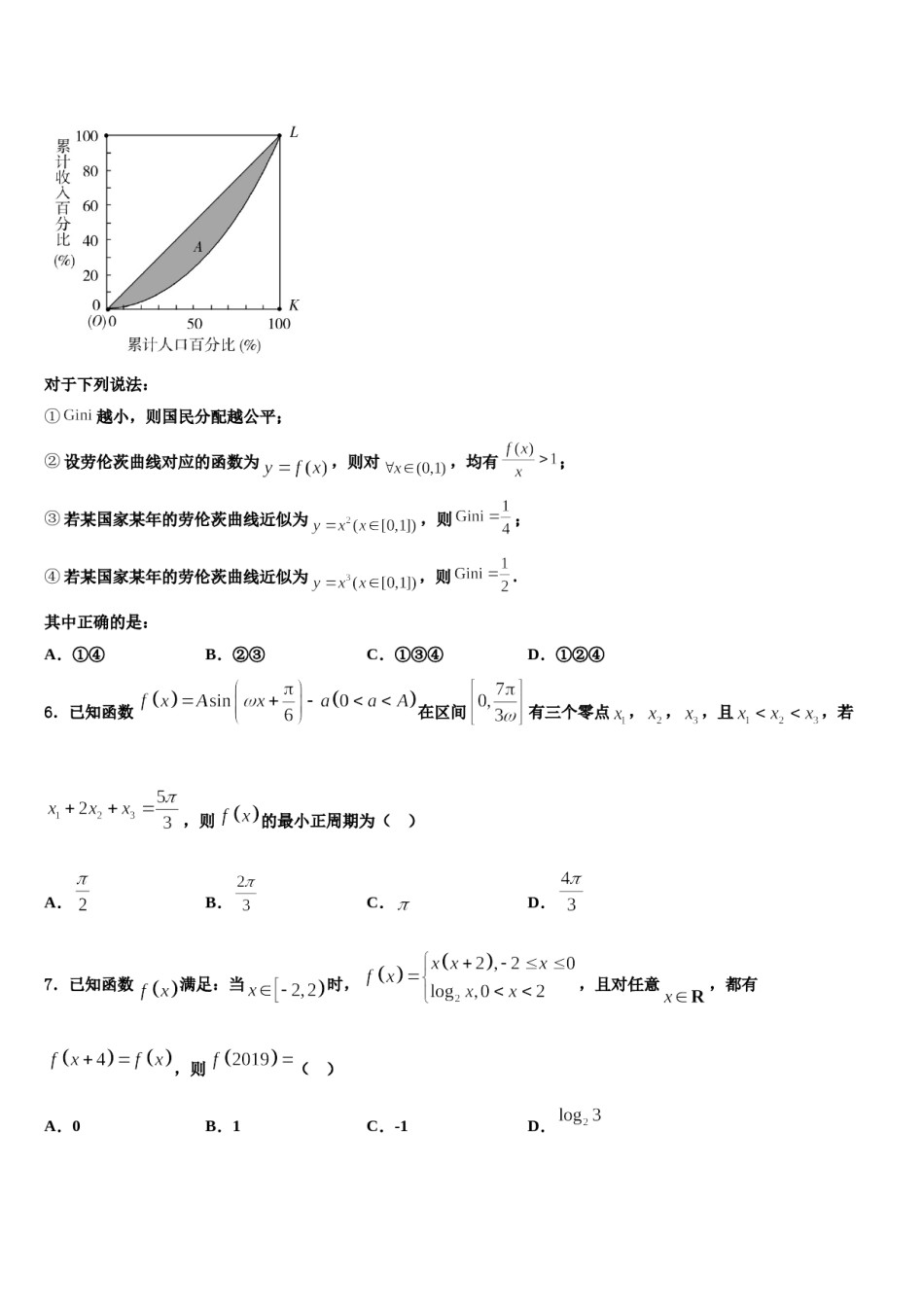
2024届云南省大理州丽江怒江高三下学期第五次调研考试数学试题注意事项:1.答题前,考生先将自己的姓名、准考证号填写清楚,将条形码准确粘贴在考生信息条形码粘贴区。2.选择题必须使用2B铅笔填涂;非选择题必须使用0.5毫米黑色字迹的签字笔书写,字体工整、笔迹清楚。3.请按照题号顺序在各题目的答题区域内作答,超出答题区域书写的答案无效;在草稿纸、试题卷上答题无效。4.保持卡面清洁,不要折叠,不要弄破、弄皱,不准使用涂改液、修正带、刮纸刀。一、选择题:本题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的。1.过圆外一点引圆的两条切线,则经过两切点的直线方程是().A.B.C.D.2.已知,则不等式的解集是()A.B.C.D.3.下列函数中,在定义域上单调递增,且值域为的是()A.B.C.D.4.如图所示的程序框图输出的是126,则①应为()A.B.C.D.5.为了研究国民收入在国民之间的分配,避免贫富过分悬殊,美国统计学家劳伦茨提出了著名的劳伦茨曲线,如图所示.劳伦茨曲线为直线时,表示收入完全平等.劳伦茨曲线为折线时,表示收入完全不平等.记区域为不平等区域,表示其面积,为的面积,将称为基尼系数.对于下列说法:,则对,均有;①越小,则国民分配越公平;②设劳伦茨曲线对应的函数为③若某国家某年的劳伦茨曲线近似为,则;④若某国家某年的劳伦茨曲线近似为,则.C.①③④D.①②④其中正确的是:B.②③A.①④6.已知函数在区间有三个零点,,,且,若,则的最小正周期为()A.B.C.D.7.已知函数满足:当时,,且对任意,都有A.0,则()D.B.1C.-18.已知函数,,若对任意的,存在实数满足,使得,则的最大值是()A.3B.2C.4D.59.已知点在双曲线上,则该双曲线的离心率为()A.B.C.D.10.已知数列满足:.若正整数使得成立,则()A.16B.17C.18D.1911.如图示,三棱锥的底面是等腰直角三角形,,且,,则与面所成角的正弦值等于()A.B.C.D.12.下列函数中,在区间上为减函数的是()A.B.C.D.二、填空题:本题共4小题,每小题5分,共20分。13.两光滑的曲线相切,那么它们在公共点处的切线方向相同.如图所示,一列圆(an>0,rn>0,n=1,2…)逐个外切,且均与曲线y=x2相切,若r1=1,则a1=___,rn=______14.在正方体中,分别为棱的中点,则直线与直线所成角的正切值为_________.中,已知,,则A的值是______.15.在16.已知实数,满足,则目标函数的最小值为__________.三、解答题:共70分。解答应写出文字说明、证明过程或演算步骤。两种,且这两种的个17.(12分)某生物硏究小组准备探究某地区蜻蜓的翼长分布规律,据统计该地区蜻蜓有体数量大致相等,记种蜻蜓和种蜻蜓的翼长(单位:)分别为随机变量,其中服从正态分布,服从正态分布.(Ⅰ)从该地区的蜻蜓中随机捕捉一只,求这只蜻蜓的翼长在区间的概率;(Ⅱ)记该地区蜻蜓的翼长为随机变量,若用正态分布来近似描述的分布,请你根据(Ⅰ)中的结果,求参数和的值(精确到0.1);的个数为,求的(Ⅲ)在(Ⅱ)的条件下,从该地区的蜻蜓中随机捕捉3只,记这3只中翼长在区间分布列及数学期望(分布列写出计算表达式即可).注:若,则,,.18.(12分)设函数.(1)当时,求不等式的解集;(2)若不等式恒成立,求实数a的取值范围.19.(12分)在中,角的对边分别为.已知,.(1)若,求;(2)求的面积的最大值.20.(12分)已知函数.(1)证明:当时,;(2)若函数有三个零点,求实数的取值范围.21.(12分)选修4-5:不等式选讲已知函数.(1)设,求不等式的解集;(2)已知,且的最小值等于,求实数的值.22.(10分)已知函数,函数在点处的切线斜率为0.(1)试用含有的式子表示,并讨论的单调性;(2)对于函数图象上的不同两点,,如果在函数图象上存在点,使得在点处的切线,则称存在“跟随切线”.特别地,当时,又称存在“中值跟随切线”.试问:函数上是否存在两点使得它存在“中值跟随切线”,若存在,求出的坐标,若不存在,说明理由.参考答案一、选择题:本题共12小题,每小题5分,共60分。在每小题给出的四个选项...