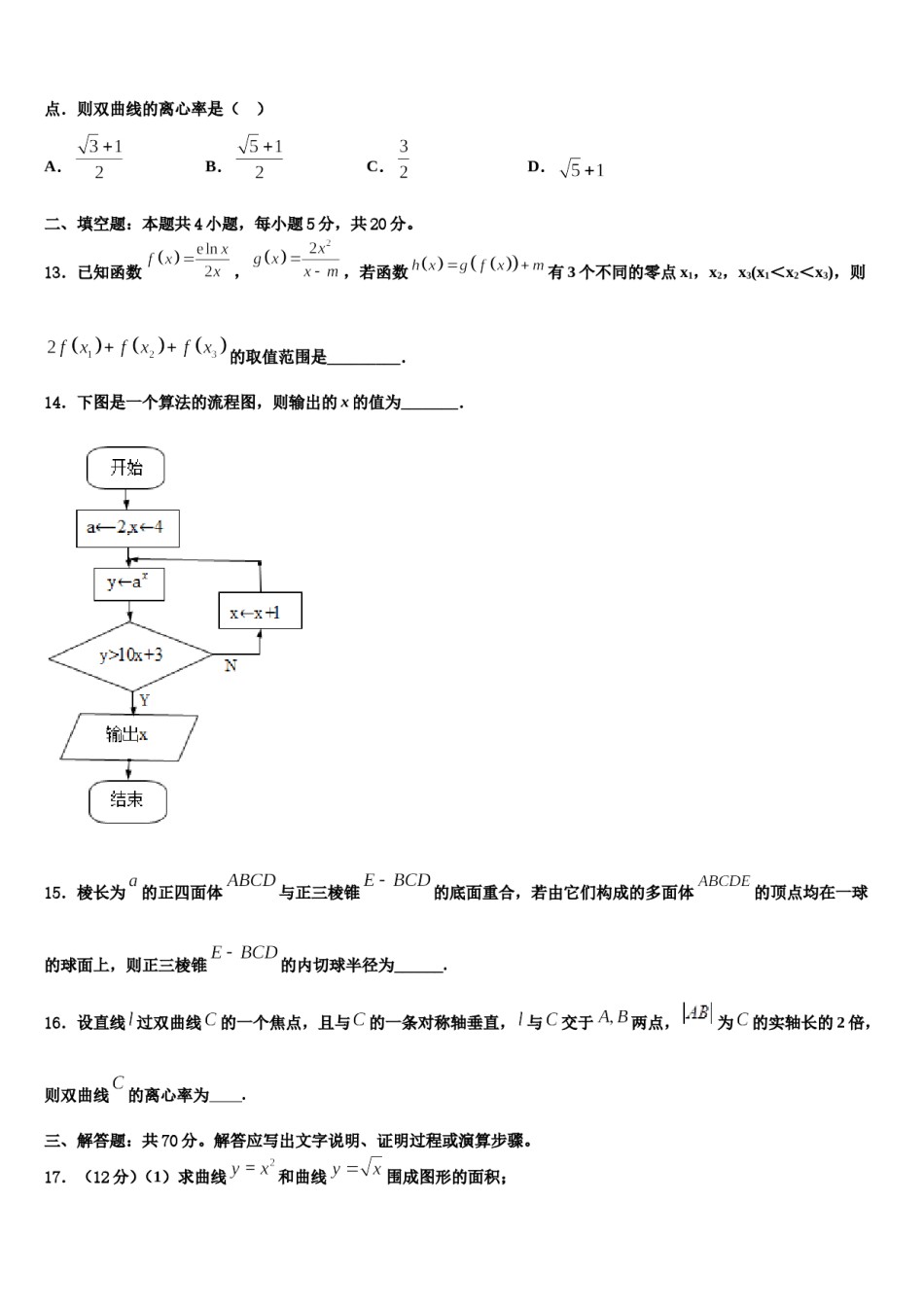
2024届北京市西城区高三下学期联考数学试题请考生注意:1.请用2B铅笔将选择题答案涂填在答题纸相应位置上,请用0.5毫米及以上黑色字迹的钢笔或签字笔将主观题的答案写在答题纸相应的答题区内。写在试题卷、草稿纸上均无效。2.答题前,认真阅读答题纸上的《注意事项》,按规定答题。一、选择题:本题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的。1.将函数的图象向右平移个周期后,所得图象关于轴对称,则的最小正值是()A.B.C.D.2.双曲线的一条渐近线方程为,那么它的离心率为()A.B.C.D.3.设直线过点,且与圆:相切于点,那么()A.B.3C.D.14.我国数学家陈景润在哥德巴赫猜想的研究中取得了世界领先的成果,哥德巴赫猜想的内容是:每个大于2的偶数都可以表示为两个素数的和,例如:,,,那么在不超过18的素数中随机选取两个不同的数,其和等于16的概率为()A.B.C.D.5.若,则“”是“的展开式中项的系数为90”的()A.必要不充分条件B.充分不必要条件C.充要条件D.既不充分也不必要条件6.集合,,则=()A.B.C.D.7.已知椭圆的中心为原点,为的左焦点,为上一点,满足且,则椭圆的方程为()A.B.C.D.8.已知圆锥的高为3,底面半径为,若该圆锥的顶点与底面的圆周都在同一个球面上,则这个球的体积与圆锥的体积的比值为()A.B.C.D.9.设分别是双曲线的左右焦点若双曲线上存在点,使,且,则双曲线的离心率为()A.B.2C.D.10.已知函数是定义在上的偶函数,当时,,则,,的大小关系为()A.B.C.D.11.如果,那么下列不等式成立的是()A.B.C.D.的焦点F重合;12.已知双曲线满足以下条件:①双曲线E的右焦点与抛物线②双曲线E与过点的幂函数的图象交于点Q,且该幂函数在点Q处的切线过点F关于原点的对称点.则双曲线的离心率是()A.B.C.D.有3个不同的零点x1,x2,x3(x1<x2<x3),则二、填空题:本题共4小题,每小题5分,共20分。13.已知函数,,若函数的取值范围是_________.14.下图是一个算法的流程图,则输出的x的值为_______.15.棱长为的正四面体与正三棱锥的底面重合,若由它们构成的多面体的顶点均在一球的球面上,则正三棱锥的内切球半径为______.16.设直线过双曲线的一个焦点,且与的一条对称轴垂直,与交于两点,为的实轴长的2倍,则双曲线的离心率为.三、解答题:共70分。解答应写出文字说明、证明过程或演算步骤。17.(12分)(1)求曲线和曲线围成图形的面积;(2)化简求值:.18.(12分)已知函数.(1)求证:当时,;(2)若对任意存在和使成立,求实数的最小值.19.(12分)已知数列,,数列满足,n.(1)若,,求数列的前2n项和;(2)若数列为等差数列,且对任意n,恒成立.①当数列为等差数列时,求证:数列,的公差相等;②数列能否为等比数列?若能,请写出所有满足条件的数列;若不能,请说明理由.20.(12分)如图,在四棱锥中,底面是直角梯形,,,,是正三角形,,是的中点.(1)证明:;(2)求直线与平面所成角的正弦值.21.(12分)已知函数.(1)当时,解关于x的不等式;(2)当时,若对任意实数,都成立,求实数的取值范围.22.(10分)选修4-5:不等式选讲已知函数f(x)=log2(x+1+x﹣2﹣m).(1)当m=7时,求函数f(x)的定义域;(2)若关于x的不等式f(x)≥2的解集是R,求m的取值范围.参考答案一、选择题:本题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的。1、D【解析】由函数的图象平移变换公式求出变换后的函数解析式,再利用诱导公式得到关于的方程,对赋值即可求解.【详解】由题意知,函数的最小正周期为,即,由函数的图象平移变换公式可得,将函数的图象向右平移个周期后的解析式为因为函数的图象关于轴对称,,,所以,即所以当时,有最小正值为.故选:D的图象平移变换公式和三角函数诱导公式及正余弦函数的性质;熟练掌握诱导公式【点睛】本题考查函数和正余弦函数的性质是求解本题的关键;属于中档题、常考题型.2、D【解析】根据双曲线的一条渐近线方程为,列出方程,求出的值即可...