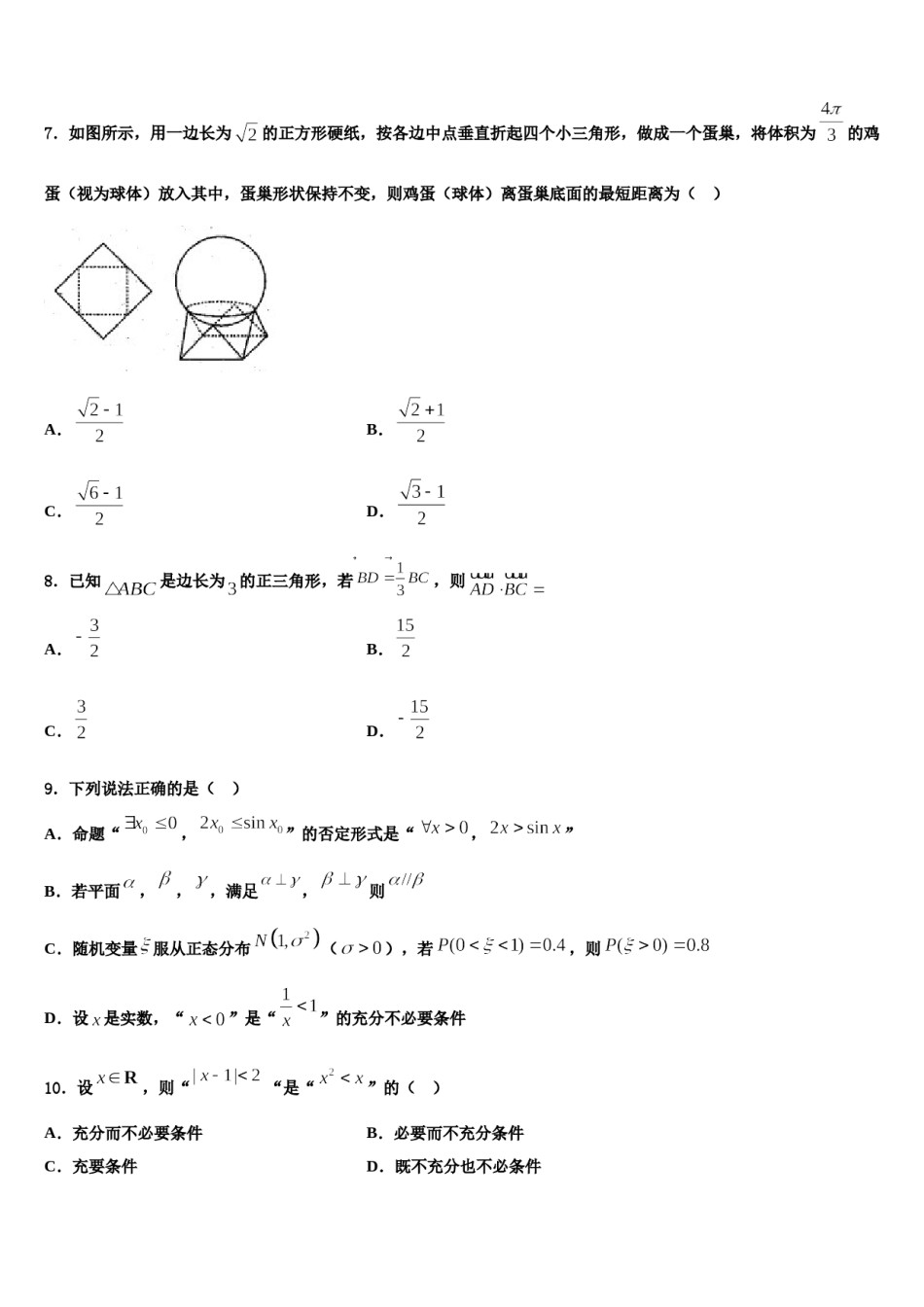
2024届四川乐山市高考仿真卷数学试题请考生注意:1.请用2B铅笔将选择题答案涂填在答题纸相应位置上,请用0.5毫米及以上黑色字迹的钢笔或签字笔将主观题的答案写在答题纸相应的答题区内。写在试题卷、草稿纸上均无效。2.答题前,认真阅读答题纸上的《注意事项》,按规定答题。一、选择题:本题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的。1.在中,“”是“为钝角三角形”的()A.充分非必要条件B.必要非充分条件C.充要条件D.既不充分也不必要条件2.三棱锥的各个顶点都在求的表面上,且是等边三角形,底面,,,若点在线段上,且,则过点的平面截球所得截面的最小面积为()A.B.C.D.3.若为过椭圆中心的弦,为椭圆的焦点,则△面积的最大值为()A.20B.30C.50D.604.若双曲线的一条渐近线与圆至多有一个交点,则双曲线的离心率的取值范围是()A.B.C.D.5.设全集,集合,,则集合()A.B.C.D.6.设α,β为两个平面,则α∥β的充要条件是A.α内有无数条直线与β平行B.α内有两条相交直线与β平行C.α,β平行于同一条直线D.α,β垂直于同一平面7.如图所示,用一边长为的正方形硬纸,按各边中点垂直折起四个小三角形,做成一个蛋巢,将体积为的鸡蛋(视为球体)放入其中,蛋巢形状保持不变,则鸡蛋(球体)离蛋巢底面的最短距离为()A.B.C.D.8.已知A.是边长为的正三角形,若,则B.C.D.9.下列说法正确的是()A.命题“,”的否定形式是“,”,则B.若平面,,,满足,则C.随机变量服从正态分布(),若D.设是实数,“”是“”的充分不必要条件10.设,则““是“”的()A.充分而不必要条件B.必要而不充分条件C.充要条件D.既不充分也不必条件11.如图所示程序框图,若判断框内为“”,则输出()A.2B.10C.34D.9812.在条件下,目标函数的最大值为40,则的最小值是()A.B.C.D.2二、填空题:本题共4小题,每小题5分,共20分。13.现有一块边长为a的正方形铁片,铁片的四角截去四个边长均为x的小正方形,然后做成一个无盖方盒,该方盒容积的最大值是________.14.在如图所示的三角形数阵中,用表示第行第个数,已知,且当时,每行中的其他各数均等于其“肩膀”上的两个数之和,即,若,则正整数的最小值为______.15.某校共有师生1600人,其中教师有1000人,现用分层抽样的方法,从所有师生中抽取一个容量为80的样本,则抽取学生的人数为_____.16.的展开式中,x5的系数是_________.(用数字填写答案)三、解答题:共70分。解答应写出文字说明、证明过程或演算步骤。17.(12分)已知曲线:和:(为参数).以原点为极点,轴的正半轴为极轴,建立极坐标系,且两种坐标系中取相同的长度单位.(1)求曲线的直角坐标方程和的方程化为极坐标方程;(2)设与,轴交于,两点,且线段的中点为.若射线与,交于,两点,求,两点间的距离.,,使得对任意两个不等的正实数,都有18.(12分)已知函数恒成立.(1)求的解析式;(2)若方程有两个实根,且,求证:.19.(12分)已知函数(1)已知直线:,:.若直线与关于对称,又函数在处的切线与垂直,求实数的值;,则当,时,求证:(2)若函数①;②.20.(12分)在中,、、的对应边分别为、、,已知,,.(1)求;中点,求的长.(2)设为21.(12分)如图,为等腰直角三角形,,D为AC上一点,将沿BD折起,得到三棱锥,且使得在底面BCD的投影E在线段BC上,连接AE.(1)证明:;(2)若,求二面角的余弦值..22.(10分)已知函数(1)当时,解不等式;(2)当时,不等式恒成立,求实数的取值范围.参考答案一、选择题:本题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的。1、C【解析】分析:从两个方向去判断,先看能推出三角形的形状是锐角三角形,而非钝角三角形,从而得到充分性不成立,再看当三角形是钝角三角形时,也推不出成立,从而必要性也不满足,从而选出正确的结,果.详解:由题意可得,在中,因为,所以,因为,所以,,结合三角形内角的条件,故A,B同为锐角,因为所以,即,所以,因此,所以...