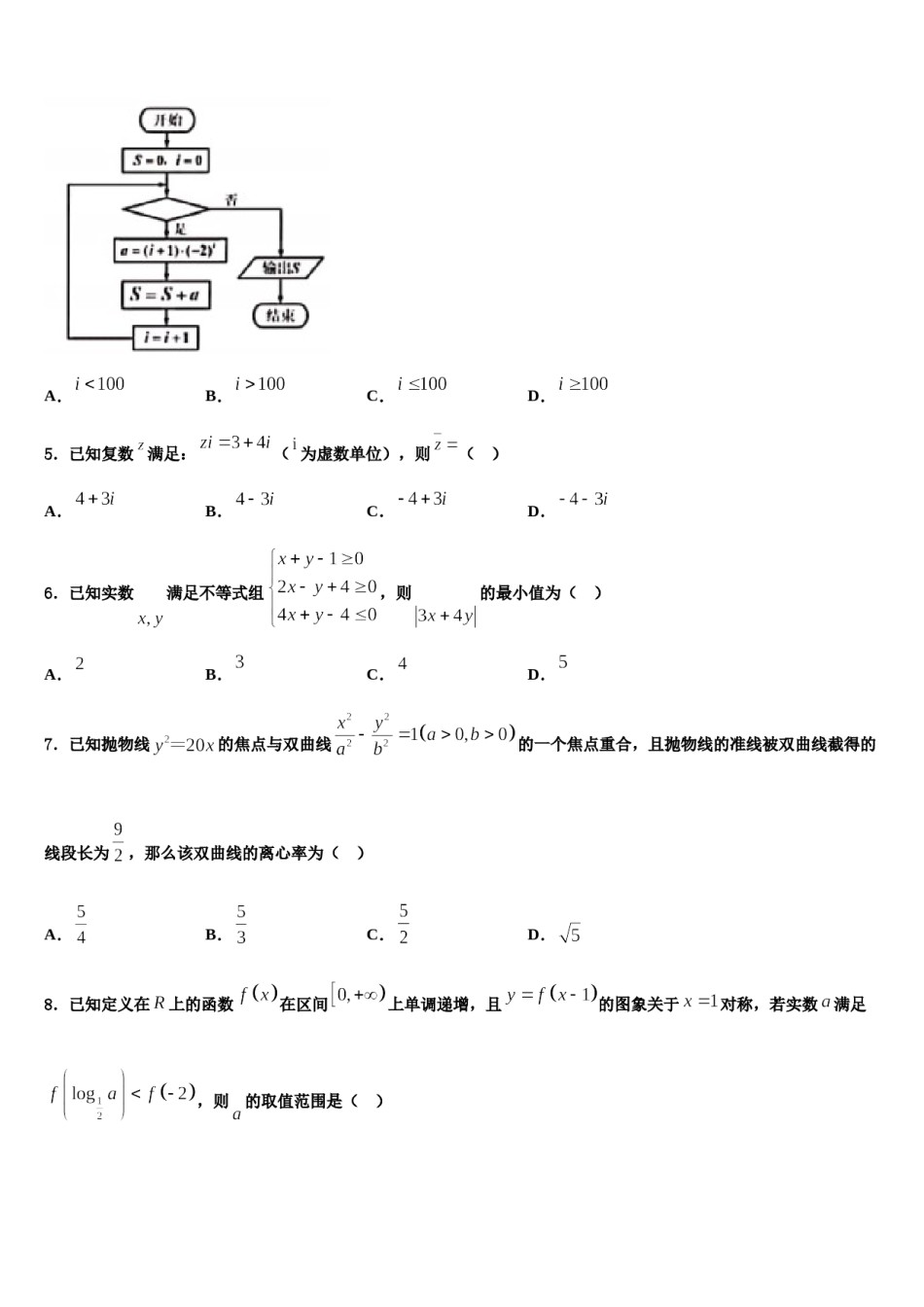
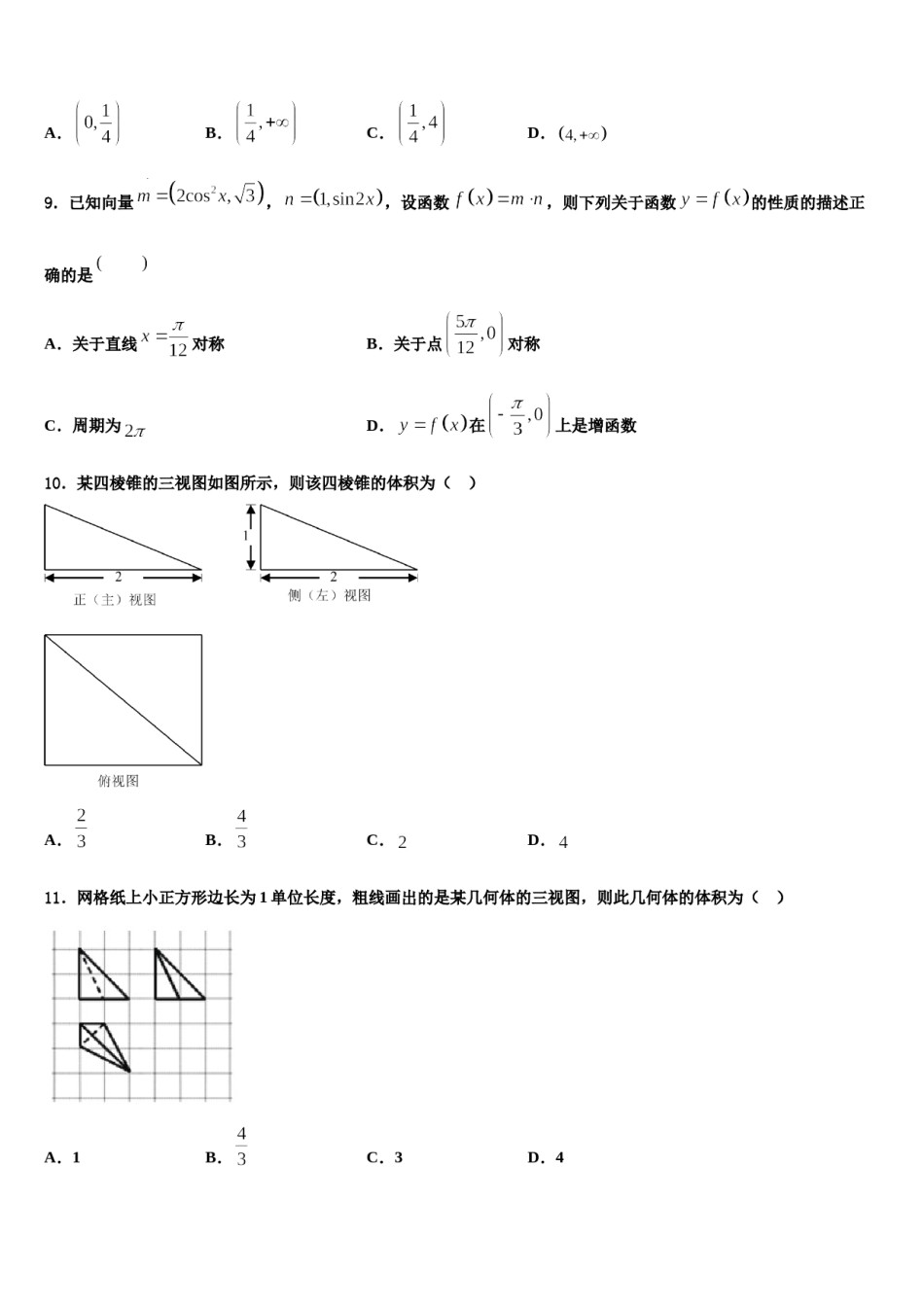
2024届四川省泸州市泸州老窖天府中学高三第三次测评数学试卷注意事项:1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其它答案标号。回答非选择题时,将答案写在答题卡上,写在本试卷上无效。3.考试结束后,将本试卷和答题卡一并交回。一、选择题:本题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的。1.如图,正方体中,,,,分别为棱、、、的中点,则下列各直线中,不与平面平行的是()A.直线B.直线C.直线D.直线2.某医院拟派2名内科医生、3名外科医生和3名护士共8人组成两个医疗分队,平均分到甲、乙两个村进行义务巡诊,其中每个分队都必须有内科医生、外科医生和护士,则不同的分配方案有A.72种B.36种C.24种D.18种3.某三棱锥的三视图如图所示,那么该三棱锥的表面中直角三角形的个数为()A.1B.2C.3D.04.为计算,设计了如图所示的程序框图,则空白框中应填入()A.B.C.D.5.已知复数满足:(为虚数单位),则()A.B.C.D.6.已知实数满足不等式组,则的最小值为()A.B.C.D.7.已知抛物线的一个焦点重合,且抛物线的准线被双曲线截得的的焦点与双曲线线段长为,那么该双曲线的离心率为()A.B.C.D.8.已知定义在上的函数在区间上单调递增,且的图象关于对称,若实数满足,则的取值范围是()A.B.C.D.,设函数,则下列关于函数9.已知向量,的性质的描述正确的是对称B.关于点对称A.关于直线C.周期为D.在上是增函数10.某四棱锥的三视图如图所示,则该四棱锥的体积为()A.B.C.D.11.网格纸上小正方形边长为1单位长度,粗线画出的是某几何体的三视图,则此几何体的体积为()A.1B.C.3D.412.已知圆截直线所得线段的长度是,则圆与圆的位置关系是()A.内切B.相交C.外切D.相离二、填空题:本题共4小题,每小题5分,共20分。13.已知集合,,则_____________.14.一个房间的地面是由12个正方形所组成,如图所示.今想用长方形瓷砖铺满地面,已知每一块长方形瓷砖可以覆盖两块相邻的正方形,即或,则用6块瓷砖铺满房间地面的方法有_______种.15.己知函数,若关于的不等式对任意的恒成立,则实数的取值范围是______.16.在△ABC中,∠BAC=,AD为∠BAC的角平分线,且,若AB=2,则BC=_______.三、解答题:共70分。解答应写出文字说明、证明过程或演算步骤。17.(12分)如图,在四棱锥中,平面,底面是矩形,,,分别是,的中点.(Ⅰ)求证:平面;(Ⅱ)设,求三棱锥的体积.18.(12分)如图,在中,,的角平分线与交于点,.(Ⅰ)求;(Ⅱ)求的面积.19.(12分)在直角坐标系xOy中,以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,已知:,:,:.(1)求与的极坐标方程,求的最大值.是矩形,四条侧棱长均相等.(2)若与交于点A,与交于点B,20.(12分)如图,在四棱锥中,底面(1)求证:平面;(2)求证:平面平面.21.(12分)如图,四棱锥中,侧面为等腰直角三角形,平面.(1)求证:平面;(2)求直线与平面所成的角的正弦值.22.(10分)的内角,,的对边分别为,,已知,.(1)求;(2)若的面积,求.参考答案一、选择题:本题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的。1、C【解析】充分利用正方体的几何特征,利用线面平行的判定定理,根据判断A的正误.根据,判断B的正误.根据与相交,判断C的正误.根据,判断D的正误.【详解】在正方体中,因为,所以平面,故A正确.因为,所以,所以平面故B正确.因为,所以平面,故D正确.因为与相交,所以与平面相交,故C错误.故选:C【点睛】本题主要考查正方体的几何特征,线面平行的判定定理,还考查了推理论证的能力,属中档题.2、B【解析】根据条件2名内科医生,每个村一名,3名外科医生和3名护士,平均分成两组,则分1名外科,2名护士和2名外科医生和1名护士,根据排列组合进行计算即可.【详解】2名内科医生,每个村一名,有2种方法,3名外科医生和3名护士,...