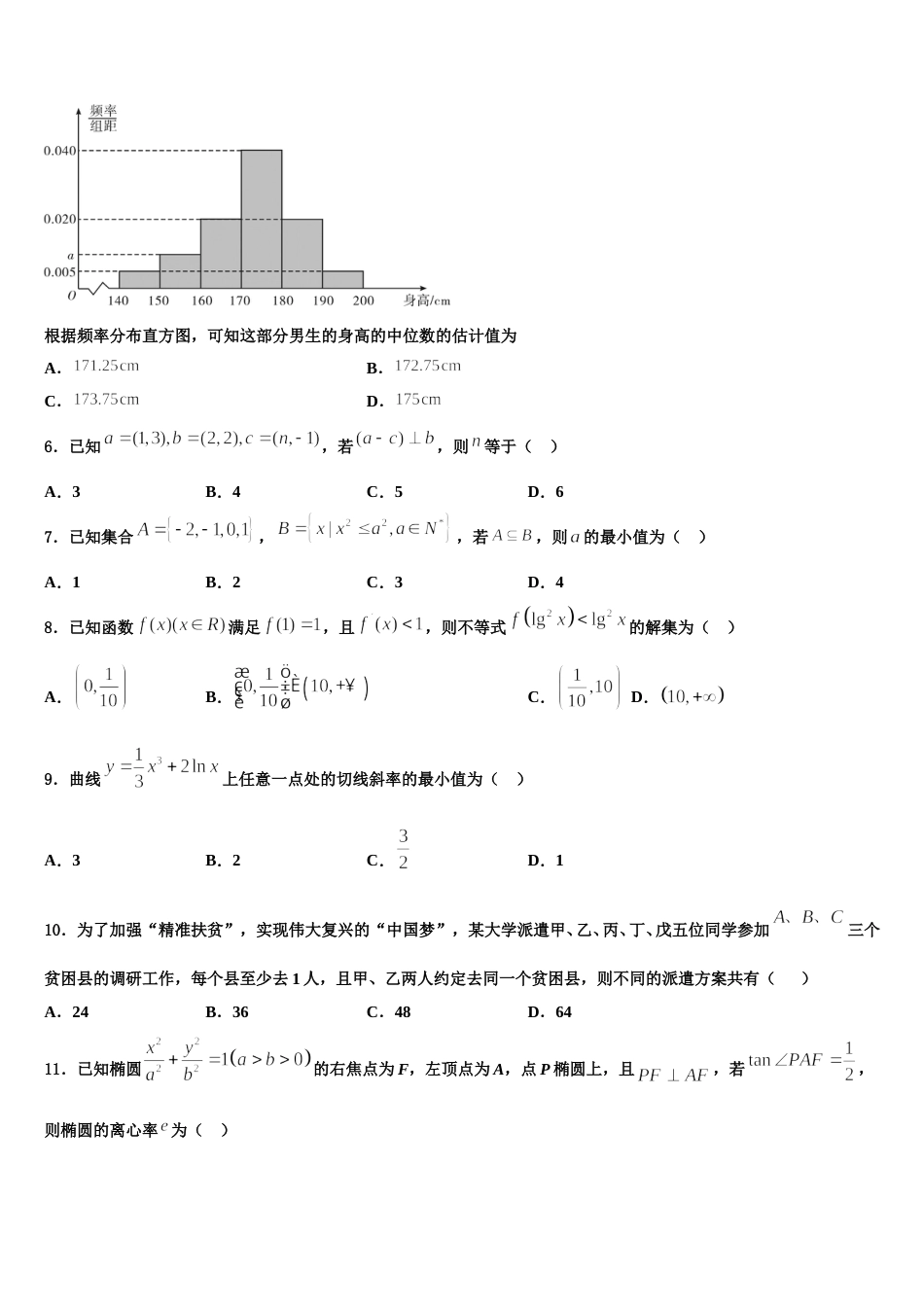
2024 届宁夏石嘴山市三中高考临考冲刺数学试卷注意事项:1. 答题前,考生先将自己的姓名、准考证号填写清楚,将条形码准确粘贴在考生信息条形码粘贴区。2.选择题必须使用 2B 铅笔填涂;非选择题必须使用 0.5 毫米黑色字迹的签字笔书写,字体工整、笔迹清楚。3.请按照题号顺序在各题目的答题区域内作答,超出答题区域书写的答案无效;在草稿纸、试题卷上答题无效。4.保持卡面清洁,不要折叠,不要弄破、弄皱,不准使用涂改液、修正带、刮纸刀。一、选择题:本题共 12 小题,每小题 5 分,共 60 分。在每小题给出的四个选项中,只有一项是符合题目要求的。1.若单位向量,夹角为,,且,则实数( )A.-1B.2C.0 或-1D.2 或-12.下列不等式成立的是( )A.B.C.D.3.已知双曲线,为坐标原点,、为其左、右焦点,点在的渐近线上,,且,则该双曲线的渐近线方程为( )A.B.C.D.4.若命题 :从有 2 件正品和 2 件次品的产品中任选 2 件得到都是正品的概率为三分之一;命题 :在边长为 4 的正方形内任取一点 ,则的概率为 ,则下列命题是真命题的是( )A. B. C. D.5.从某市的中学生中随机调查了部分男生,获得了他们的身高数据,整理得到如下频率分布直方图:根据频率分布直方图,可知这部分男生的身高的中位数的估计值为A.B.C.D.6.已知,若,则等于( )A.3B.4C.5D.67.已知集合,,若,则的最小值为( )A.1B.2C.3D.48.已知函数满足,且,则不等式的解集为( )A.B.C.D.9.曲线上任意一点处的切线斜率的最小值为( )A.3B.2C.D.110.为了加强“精准扶贫”,实现伟大复兴的“中国梦”,某大学派遣甲、乙、丙、丁、戊五位同学参加三个贫困县的调研工作,每个县至少去 1 人,且甲、乙两人约定去同一个贫困县,则不同的派遣方案共有( )A.24B.36C.48D.6411.已知椭圆的右焦点为 F,左顶点为 A,点 P 椭圆上,且,若,则椭圆的离心率 为( )A.B.C.D.12.已知函数,,且在上是单调函数,则下列说法正确的是( )A.B.C.函数在上单调递减D.函数的图像关于点对称二、填空题:本题共 4 小题,每小题 5 分,共 20 分。13.(5 分)有一道描述有关等差与等比数列的问题:有四个和尚在做法事之前按身高从低到高站成一列,已知前三个和尚的身高依次成等差数列,后三个和尚的身高依次成等比数列,且前三个和尚的身高之和为cm,中间两个和尚的身高之和为cm,则最高的和尚的身高是____________ cm.14.函数的图象在处的切线方程为__________.15.某中学数学竞赛培训班共有 10 人,分为甲、乙两个小组,在一次阶段测试中两个小组成绩的茎叶图如图所示,若甲组 5 名同学成绩的平均数为 81,乙组 5 名同学成绩的中位数为 73,则 x- y 的值为________.16.已知为矩形的对角线的交点,现从这 5 个点中任选 3 个点,则这 3 个点不共线的概率为________.三、解答题:共 70 分。解答应写出文字说明、证明过程或演算步骤。17.(12 分)过点作倾斜角为的直线与曲线(为参数)相交于 M、N 两点.(1)写出曲线 C 的一般方程;(2)求的最小值.18.(12 分)某商场举行优惠促销活动,顾客仅可以从以下两种优惠方案中选择一种.方案一:每满 100 元减 20 元;方案二:满 100 元可抽奖一次.具体规则是从装有 2 个红球、2 个白球的箱子随机取出 3 个球(逐个有放回地抽取),所得结果和享受的优惠如下表:(注:所有小球仅颜色有区别)红球个数3210实际付款7 折8 折9 折原价(1)该商场某顾客购物金额超过 100 元,若该顾客选择方案二,求该顾客获得 7 折或 8 折优惠的概率;(2)若某顾客购物金额为 180 元,选择哪种方案更划算?19.(12 分)已知函数.(1)讨论函数的极值;(2)记关于的方程的两根分别为,求证:.20.(12 分)某房地产开发商在其开发的某小区前修建了一个弓形景观湖.如图,该弓形所在的圆是以为直径的圆,且米,景观湖边界与平行且它们间的距离为米.开发商计划从点出发建一座景观桥(假定建成的景观桥的桥面与地面和...