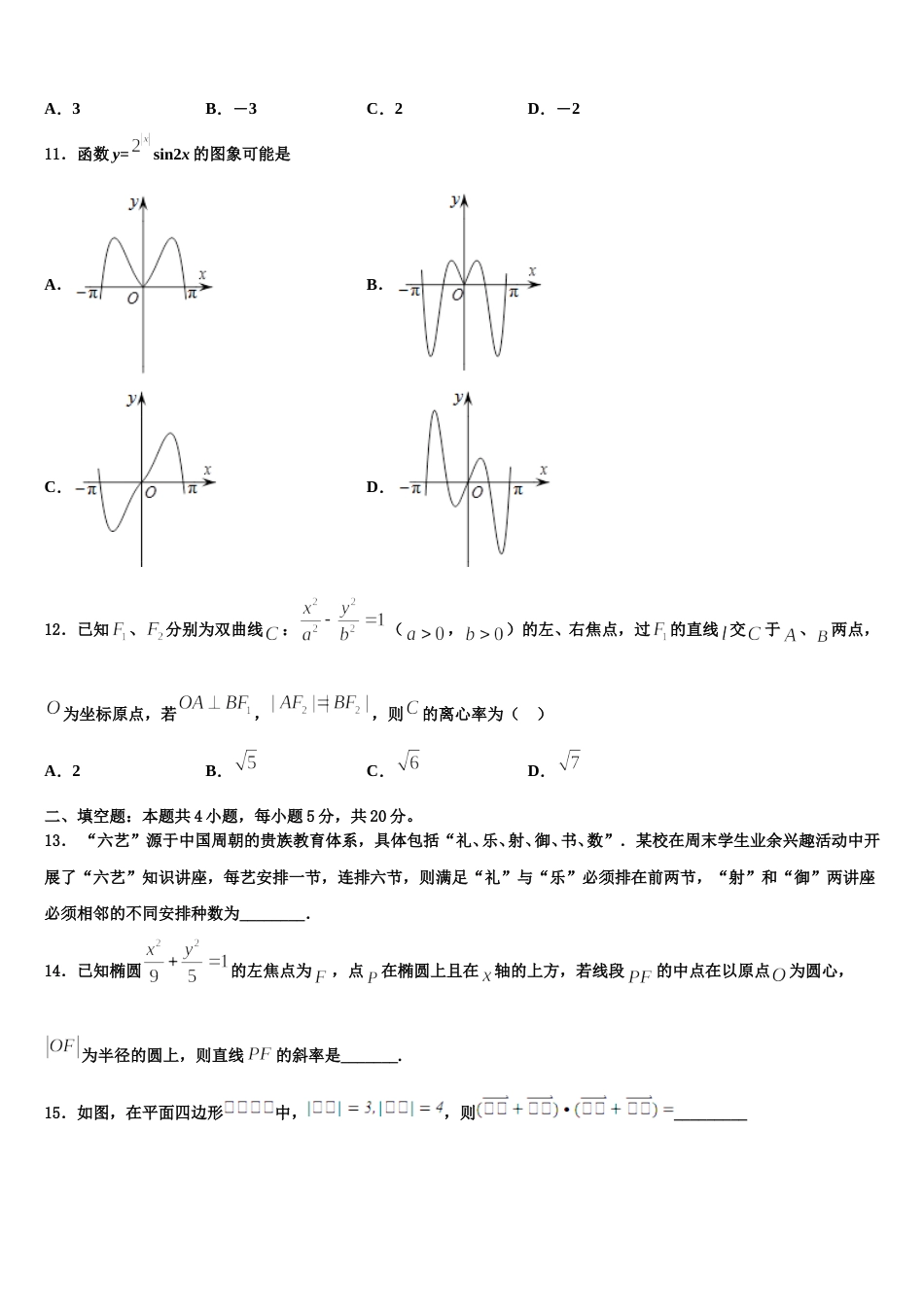
2024 届山西省忻州一中等四校重点中学高考考前提分数学仿真卷注意事项1.考试结束后,请将本试卷和答题卡一并交回.2.答题前,请务必将自己的姓名、准考证号用 0.5 毫米黑色墨水的签字笔填写在试卷及答题卡的规定位置.3.请认真核对监考员在答题卡上所粘贴的条形码上的姓名、准考证号与本人是否相符.4.作答选择题,必须用 2B 铅笔将答题卡上对应选项的方框涂满、涂黑;如需改动,请用橡皮擦干净后,再选涂其他答案.作答非选择题,必须用 05 毫米黑色墨水的签字笔在答题卡上的指定位置作答,在其他位置作答一律无效.5.如需作图,须用 2B 铅笔绘、写清楚,线条、符号等须加黑、加粗.一、选择题:本题共 12 小题,每小题 5 分,共 60 分。在每小题给出的四个选项中,只有一项是符合题目要求的。1.若复数( 是虚数单位),则复数在复平面内对应的点位于( )A.第一象限B.第二象限C.第三象限D.第四象限2.设等差数列的前 n 项和为,且,,则( )A.9B.12C.D.3.设、,数列满足,,,则( )A.对于任意,都存在实数,使得恒成立B.对于任意,都存在实数,使得恒成立C.对于任意,都存在实数,使得恒成立D.对于任意,都存在实数,使得恒成立4.已知各项都为正的等差数列中,,若,,成等比数列,则( )A.B.C.D.5.已知分别为双曲线的左、右焦点,点是其一条渐近线上一点,且以为直径的圆经过点,若的面积为,则双曲线的离心率为( )A.B.C.D.6.设函数定义域为全体实数,令.有以下 6 个论断:①是奇函数时,是奇函数;②是偶函数时,是奇函数;③是偶函数时,是偶函数;④是奇函数时,是偶函数⑤是偶函数;⑥ 对任意的实数,.那么正确论断的编号是( )A.③④B.①②⑥C.③④⑥D.③④⑤7.记递增数列的前项和为.若,,且对中的任意两项与(),其和,或其积,或其商仍是该数列中的项,则( )A.B.C.D.8.已知全集为,集合,则( )A.B.C.D.9.设,,,则,,三数的大小关系是A.B.C.D.10.函数在内有且只有一个零点,则 a 的值为( )A.3B.-3C.2D.-211.函数 y=sin2x 的图象可能是A.B.C.D.12.已知、分别为双曲线:(,)的左、右焦点,过的直线 交于、两点,为坐标原点,若,,则的离心率为( )A.2B.C.D.二、填空题:本题共 4 小题,每小题 5 分,共 20 分。13. “六艺”源于中国周朝的贵族教育体系,具体包括“礼、乐、射、御、书、数”.某校在周末学生业余兴趣活动中开展了“六艺”知识讲座,每艺安排一节,连排六节,则满足“礼”与“乐”必须排在前两节,“射”和“御”两讲座必须相邻的不同安排种数为________.14.已知椭圆的左焦点为,点在椭圆上且在轴的上方,若线段的中点在以原点为圆心,为半径的圆上,则直线的斜率是_______.15.如图,在平面四边形中,,则_________16.有以下四个命题:①在中,的充要条件是;②函数在区间上存在零点的充要条件是;③对于函数,若,则必不是奇函数;④函数与的图象关于直线对称.其中正确命题的序号为______.三、解答题:共 70 分。解答应写出文字说明、证明过程或演算步骤。17.(12 分)已知集合,集合,.(1)求集合 B;(2)记,且集合 M 中有且仅有一个整数,求实数 k 的取值范围.18.(12 分)已知函数,.(1)求证:在区间上有且仅有一个零点,且;(2)若当时,不等式恒成立,求证:.19.(12 分)设抛物线的焦点为,准线为 ,为抛物线过焦点的弦,已知以为直径的圆与 相切于点.(1)求的值及圆的方程;(2)设为 上任意一点,过点作的切线,切点为,证明:.20.(12 分)如图,是矩形,的顶点在边上,点,分别是,上的动点(的长度满足需求).设,,,且满足.(1)求;(2)若,,求的最大值.21.(12 分)在平面直角坐标系中,直线 的参数方程为( 为参数),以坐标原点为极点,轴的正半轴为极轴建立极坐标系,曲线的极坐标方程为.(1)求直线 的普通方程和曲线的直角坐标方程;(2)若直线 与曲线交于、两点,求的面积.22.(10 分)2018 年 9 月,台风“山竹”在我国多个省市登陆,造成直接经...