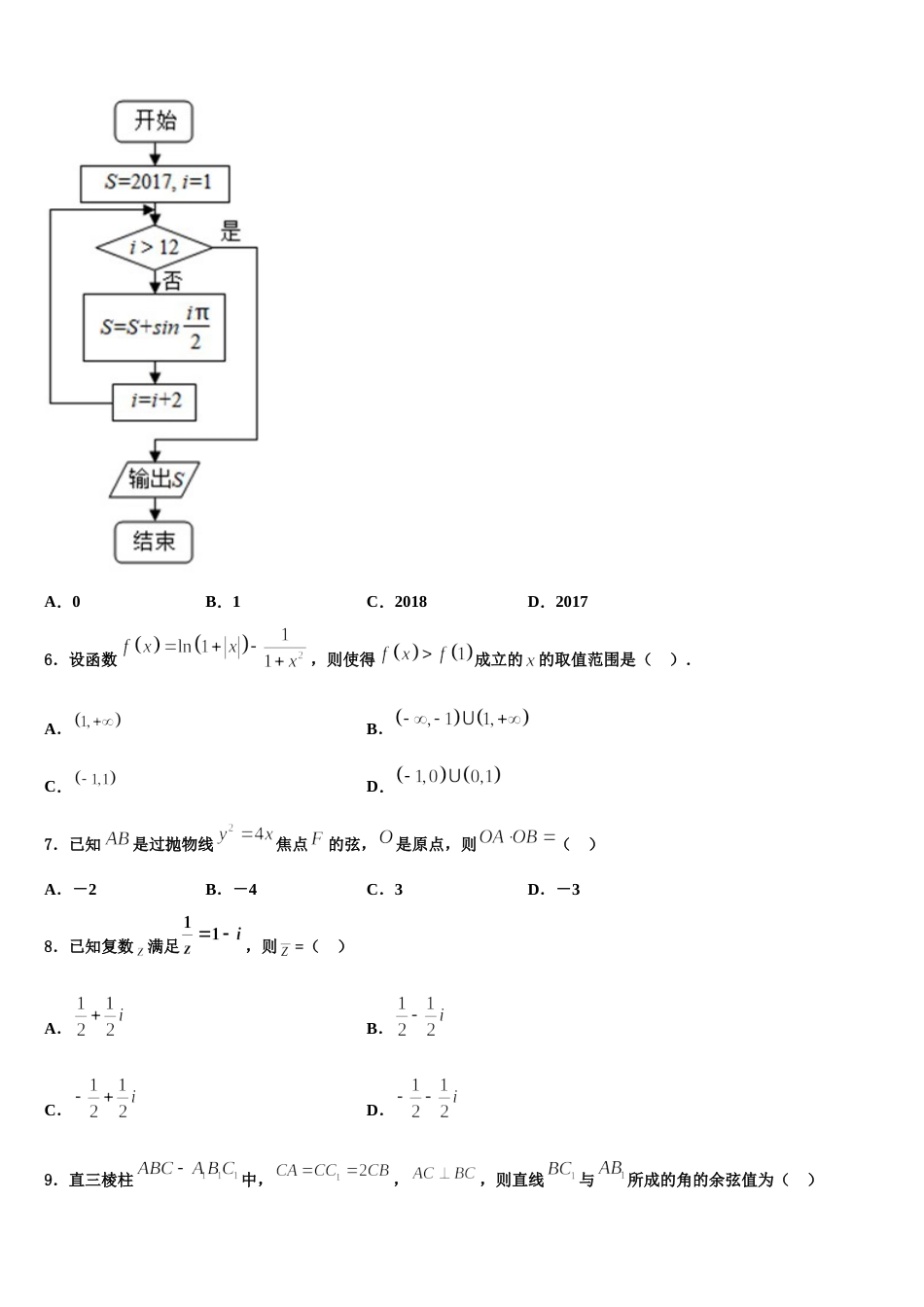
2024 届山西省阳泉市重点中学高三六校第一次联考数学试卷请考生注意:1.请用 2B 铅笔将选择题答案涂填在答题纸相应位置上,请用 0.5 毫米及以上黑色字迹的钢笔或签字笔将主观题的答案写在答题纸相应的答题区内。写在试题卷、草稿纸上均无效。2.答题前,认真阅读答题纸上的《注意事项》,按规定答题。一、选择题:本题共 12 小题,每小题 5 分,共 60 分。在每小题给出的四个选项中,只有一项是符合题目要求的。1.已知、是双曲线的左右焦点,过点与双曲线的一条渐近线平行的直线交双曲线另一条渐近线于点,若点在以线段为直径的圆外,则双曲线离心率的取值范围是( )A.B.C.D.2.正三棱柱中,,是的中点,则异面直线与所成的角为( )A.B.C.D.3.在中,“”是“”的( )A.充分而不必要条件B.必要而不充分条件C.充分必要条件D.既不充分也不必要条件4.已知双曲线的左、右顶点分别是,双曲线的右焦点为,点在过且垂直于轴的直线 上,当的外接圆面积达到最小时,点恰好在双曲线上,则该双曲线的方程为( )A.B.C.D.5.运行如图程序,则输出的 S 的值为( ) A.0B.1C.2018D.20176.设函数,则使得成立的的取值范围是( ).A.B.C.D.7.已知是过抛物线焦点的弦,是原点,则( )A.-2B.-4C.3D.-38.已知复数满足,则=( )A.B.C.D.9.直三棱柱中,,,则直线与所成的角的余弦值为( )A.B.C.D.10.在平面直角坐标系中,经过点,渐近线方程为的双曲线的标准方程为( )A.B.C.D.11.已知函数的图象向左平移个单位后得到函数的图象,则的最小值为( )A.B.C.D.12.盒中有 6 个小球,其中 4 个白球,2 个黑球,从中任取个球,在取出的球中,黑球放回,白球则涂黑后放回,此时盒中黑球的个数,则( )A.,B.,C.,D.,二、填空题:本题共 4 小题,每小题 5 分,共 20 分。13.已知曲线,点,在曲线上,且以为直径的圆的方程是.则_______.14.根据如图所示的伪代码,若输入的的值为 2,则输出的的值为____________.15.古代“五行”学认为:“物质分金、木、土、水、火五种属性,金克木,木克土,土克水,水克火,火克金.”将五种不同属性的物质任意排成一列,但排列中属性相克的两种物质不相邻,则这样的排列方法有_________种. (用数字作答)16.已知双曲线的左右焦点为,过作轴的垂线与相交于两点,与轴相交于.若,则双曲线的离心率为_________.三、解答题:共 70 分。解答应写出文字说明、证明过程或演算步骤。17.(12 分)已知点是抛物线的顶点,,是上的两个动点,且.(1)判断点是否在直线上?说明理由;(2)设点是△的外接圆的圆心,点到轴的距离为,点,求的最大值.18.(12 分)追求人类与生存环境的和谐发展是中国特色社会主义生态文明的价值取向.为了改善空气质量,某城市环保局随机抽取了一年内 100 天的空气质量指数(AQI)的检测数据,结果统计如表:AQI空气质量优良轻度污染中度污染重度污染重度污染天数61418272510(1)从空气质量指数属于[0,50],(50,100]的天数中任取 3 天,求这 3 天中空气质量至少有 2 天为优的概率;(2)已知某企业每天因空气质量造成的经济损失 y(单位:元)与空气质量指数 x 的关系式为,假设该企业所在地 7 月与 8 月每天空气质量为优、良、轻度污染、中度污染、重度污染、严重污染的概率分别为.9 月每天的空气质量对应的概率以表中 100 天的空气质量的频率代替.(i)记该企业 9 月每天因空气质量造成的经济损失为 X 元,求 X 的分布列;(ii)试问该企业 7 月、8 月、9 月这三个月因空气质量造成的经济损失总额的数学期望是否会超过 2.88 万元?说明你的理由.19.(12 分)在中,内角 A,B,C 的对边分别为 a,b,c,且满足.(1)求 B;(2)若,AD 为 BC 边上的中线,当的面积取得最大值时,求 AD 的长.20.(12 分)已知等比数列中,,是和的等差中项.(1)求数列的通项公式;(2)记,求数列的前项和.21.(12 分)已知直线 与抛物线交于两点.(1)当点的横坐标之和为 4 时,求直线 的...