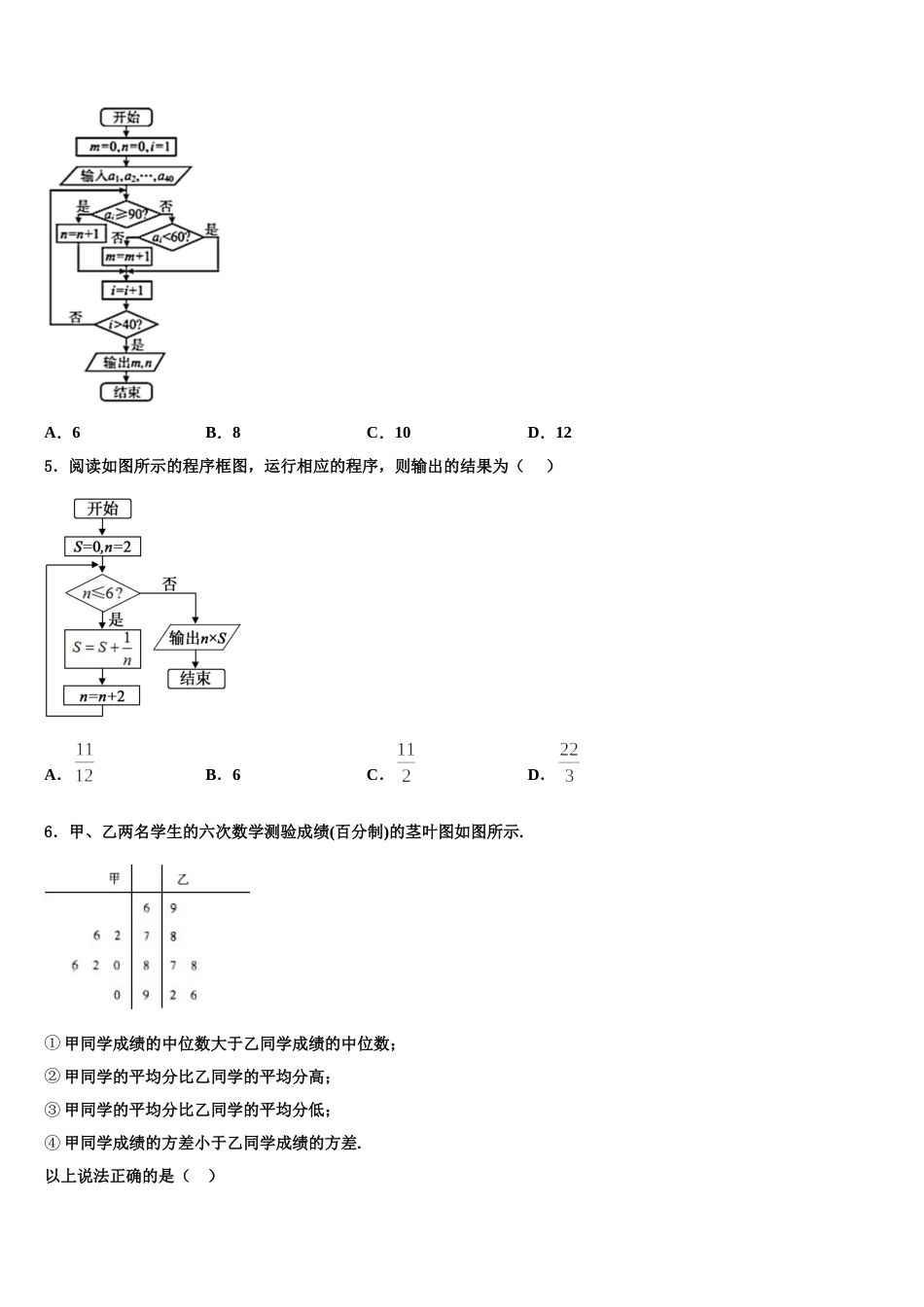
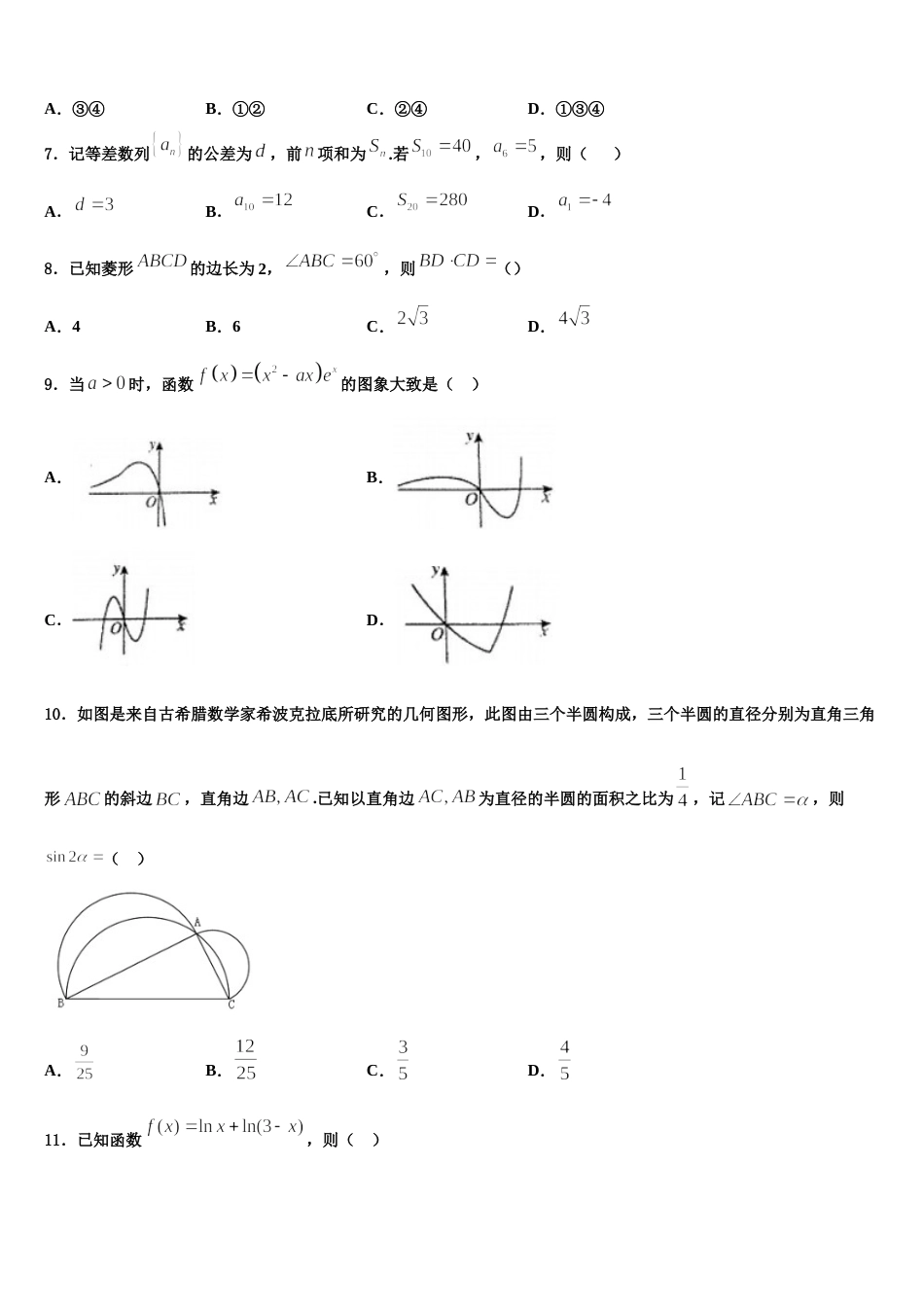
2024 届广东佛山顺德区高三最后一模数学试题注意事项1.考生要认真填写考场号和座位序号。2.试题所有答案必须填涂或书写在答题卡上,在试卷上作答无效。第一部分必须用 2B 铅笔作答;第二部分必须用黑色字迹的签字笔作答。3.考试结束后,考生须将试卷和答题卡放在桌面上,待监考员收回。一、选择题:本题共 12 小题,每小题 5 分,共 60 分。在每小题给出的四个选项中,只有一项是符合题目要求的。1.若复数 z 满足,则( )A.B.C.D.2.设,分别是椭圆的左、右焦点,过的直线交椭圆于,两点,且,,则椭圆的离心率为( )A.B.C.D.3.若,则函数在区间内单调递增的概率是( )A. B. C. D.4.某校在高一年级进行了数学竞赛(总分 100 分),下表为高一·一班 40 名同学的数学竞赛成绩:555759616864625980889895607388748677799497100999789818060796082959093908580779968如图的算法框图中输入的为上表中的学生的数学竞赛成绩,运行相应的程序,输出,的值,则( )A.6B.8C.10D.125.阅读如图所示的程序框图,运行相应的程序,则输出的结果为( )A.B.6C.D.6.甲、乙两名学生的六次数学测验成绩(百分制)的茎叶图如图所示.① 甲同学成绩的中位数大于乙同学成绩的中位数;② 甲同学的平均分比乙同学的平均分高;③ 甲同学的平均分比乙同学的平均分低;④ 甲同学成绩的方差小于乙同学成绩的方差.以上说法正确的是( )A.③④B.①②C.②④D.①③④7.记等差数列的公差为,前项和为.若,,则( )A.B.C.D.8.已知菱形的边长为 2,,则()A.4B.6C.D.9.当时,函数的图象大致是( )A.B.C.D.10.如图是来自古希腊数学家希波克拉底所研究的几何图形,此图由三个半圆构成,三个半圆的直径分别为直角三角形的斜边,直角边.已知以直角边为直径的半圆的面积之比为,记,则( )A.B.C.D.11.已知函数,则( )A.函数在上单调递增B.函数在上单调递减C.函数图像关于对称D.函数图像关于对称12.已知函数的图像与一条平行于轴的直线有两个交点,其横坐标分别为,则( )A.B.C.D.二、填空题:本题共 4 小题,每小题 5 分,共 20 分。13.某校共有师生 1600 人,其中教师有 1000 人,现用分层抽样的方法,从所有师生中抽取一个容量为 80 的样本,则抽取学生的人数为_____.14.已知等差数列满足,,则的值为________.15.如图,在中,已知,为边的中点.若,垂足为,则的值为__. 16.曲线在处的切线方程是_________.三、解答题:共 70 分。解答应写出文字说明、证明过程或演算步骤。17.(12 分)已知函数.(1)若,,求函数的单调区间;(2)时,若对一切恒成立,求 a 的取值范围.18.(12 分)某商店举行促销反馈活动,顾客购物每满 200 元,有一次抽奖机会(即满 200 元可以抽奖一次,满 400元可以抽奖两次,依次类推).抽奖的规则如下:在一个不透明口袋中装有编号分别为 1,2,3,4,5 的 5 个完全相同的小球,顾客每次从口袋中摸出一个小球,共摸三次,每次摸出的小球均不放回口袋,若摸得的小球编号一次比一次大(如 1,2,5),则获得一等奖,奖金 40 元;若摸得的小球编号一次比一次小(如 5,3,1),则获得二等奖,奖金 20 元;其余情况获得三等奖,奖金 10 元.(1)某人抽奖一次,求其获奖金额 X 的概率分布和数学期望;(2)赵四购物恰好满 600 元,假设他不放弃每次抽奖机会,求他获得的奖金恰好为 60 元的概率.19.(12 分)在某外国语学校举行的(高中生数学建模大赛)中,参与大赛的女生与男生人数之比为,且成绩分布在,分数在以上(含)的同学获奖.按女生、男生用分层抽样的方法抽取人的成绩作为样本,得到成绩的频率分布直方图如图所示.( )Ⅰ 求的值,并计算所抽取样本的平均值(同一组中的数据用该组区间的中点值作代表);()Ⅱ 填写下面的列联表,并判断在犯错误的概率不超过的前提下能否认为“获奖与女生、男生有关”.女生男生总计获奖不获奖总计附表及公式:其中,.20.(12 分)在中,角,,所对的边分别是,,,且.(1)求的值;(2)若,求的取值...