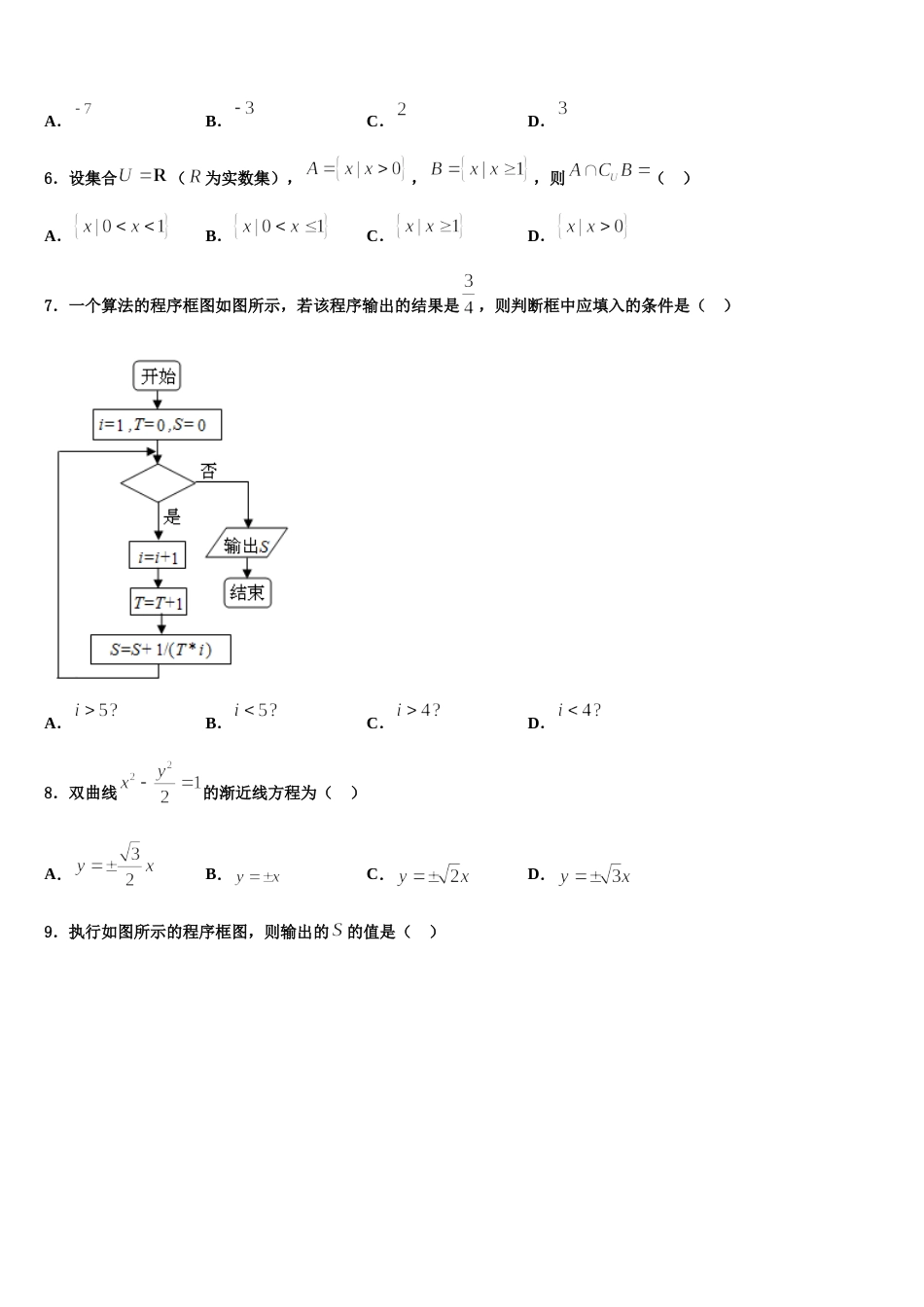
2024 届广东揭阳市惠来县第一中学高考数学倒计时模拟卷注意事项1.考试结束后,请将本试卷和答题卡一并交回.2.答题前,请务必将自己的姓名、准考证号用 0.5 毫米黑色墨水的签字笔填写在试卷及答题卡的规定位置.3.请认真核对监考员在答题卡上所粘贴的条形码上的姓名、准考证号与本人是否相符.4.作答选择题,必须用 2B 铅笔将答题卡上对应选项的方框涂满、涂黑;如需改动,请用橡皮擦干净后,再选涂其他答案.作答非选择题,必须用 05 毫米黑色墨水的签字笔在答题卡上的指定位置作答,在其他位置作答一律无效.5.如需作图,须用 2B 铅笔绘、写清楚,线条、符号等须加黑、加粗.一、选择题:本题共 12 小题,每小题 5 分,共 60 分。在每小题给出的四个选项中,只有一项是符合题目要求的。1.定义在上的函数满足,则()A.-1B.0C.1D.22.已知函数,要得到函数的图象,只需将的图象( )A.向左平移个单位长度B.向右平移个单位长度C.向左平移个单位长度D.向右平移个单位长度3.第 24 届冬奥会将于 2022 年 2 月 4 日至 2 月 20 日在北京市和张家口市举行,为了解奥运会会旗中五环所占面积与单独五个环面积之和的比值 P,某学生做如图所示的模拟实验:通过计算机模拟在长为 10,宽为 6 的长方形奥运会旗内随机取 N 个点,经统计落入五环内部及其边界上的点数为 n 个,已知圆环半径为 1,则比值 P 的近似值为( )A.B.C.D.4.若复数 z 满足,则复数 z 在复平面内对应的点在( )A.第一象限B.第二象限C.第三象限D.第四象限5.已知平面向量满足与的夹角为,且,则实数的值为( )A.B.C.D.6.设集合(为实数集),,,则( )A.B.C.D.7.一个算法的程序框图如图所示,若该程序输出的结果是,则判断框中应填入的条件是( )A.B.C.D.8.双曲线的渐近线方程为( )A.B.C.D.9.执行如图所示的程序框图,则输出的的值是( )A.8B.32C.64D.12810.已知函数为奇函数,且,则( )A.2B.5C.1D.311.已知等差数列的公差为-2,前项和为,若,,为某三角形的三边长,且该三角形有一个内角为,则的最大值为( )A.5B.11C.20D.2512.在各项均为正数的等比数列中,若,则( )A.B.6C.4D.5二、填空题:本题共 4 小题,每小题 5 分,共 20 分。13.若向量与向量垂直,则______.14.已知实数,且由的最大值是_________15.某校初三年级共有名女生,为了了解初三女生 分钟“仰卧起坐”项目训练情况,统计了所有女生 分钟“仰卧起坐”测试数据(单位:个),并绘制了如下频率分布直方图,则 分钟至少能做到个仰卧起坐的初三女生有_____________个.16.如图,在梯形中,∥,分别是的中点,若,则的值为___________.三、解答题:共 70 分。解答应写出文字说明、证明过程或演算步骤。17.(12 分)已知数列{an}满足条件,且 an+2=(﹣1)n(an1﹣ )+2an+1,n∈N*.(Ⅰ)求数列{an}的通项公式;(Ⅱ)设 bn=,Sn为数列{bn}的前 n 项和,求证:Sn.18.(12 分)在三角形 ABC 中,角 A,B,C 的对边分别为 a,b,c,若,角为钝角, (1)求的值; (2)求边的长.19.(12 分)2019 年 12 月以来,湖北省武汉市持续开展流感及相关疾病监测,发现多起病毒性肺炎病例,均诊断为病毒性肺炎/肺部感染,后被命名为新型冠状病毒肺炎(CoronaVirusDisease2019,COVID—19),简称“新冠肺炎”.下图是 2020 年 1 月 15 日至 1 月 24 日累计确诊人数随时间变化的散点图.为了预测在未釆取强力措施下,后期的累计确诊人数,建立了累计确诊人数 y 与时间变量 t 的两个回归模型,根据 1月 15 日至 1 月 24 日的数据(时间变量 t 的值依次 1,2,…,10)建立模型和.(1)根据散点图判断,与哪一个适宜作为累计确诊人数 y 与时间变量 t 的回归方程类型?(给出判断即可,不必说明理由)(2 根据(1)的判断结果及附表中数据,建立 y 关于 x 的回归方程;(3)以下是 1 月 25 日至 1 月 29 日累计确诊人数的真实数据,根据(2)的结果回答下列问题:时...