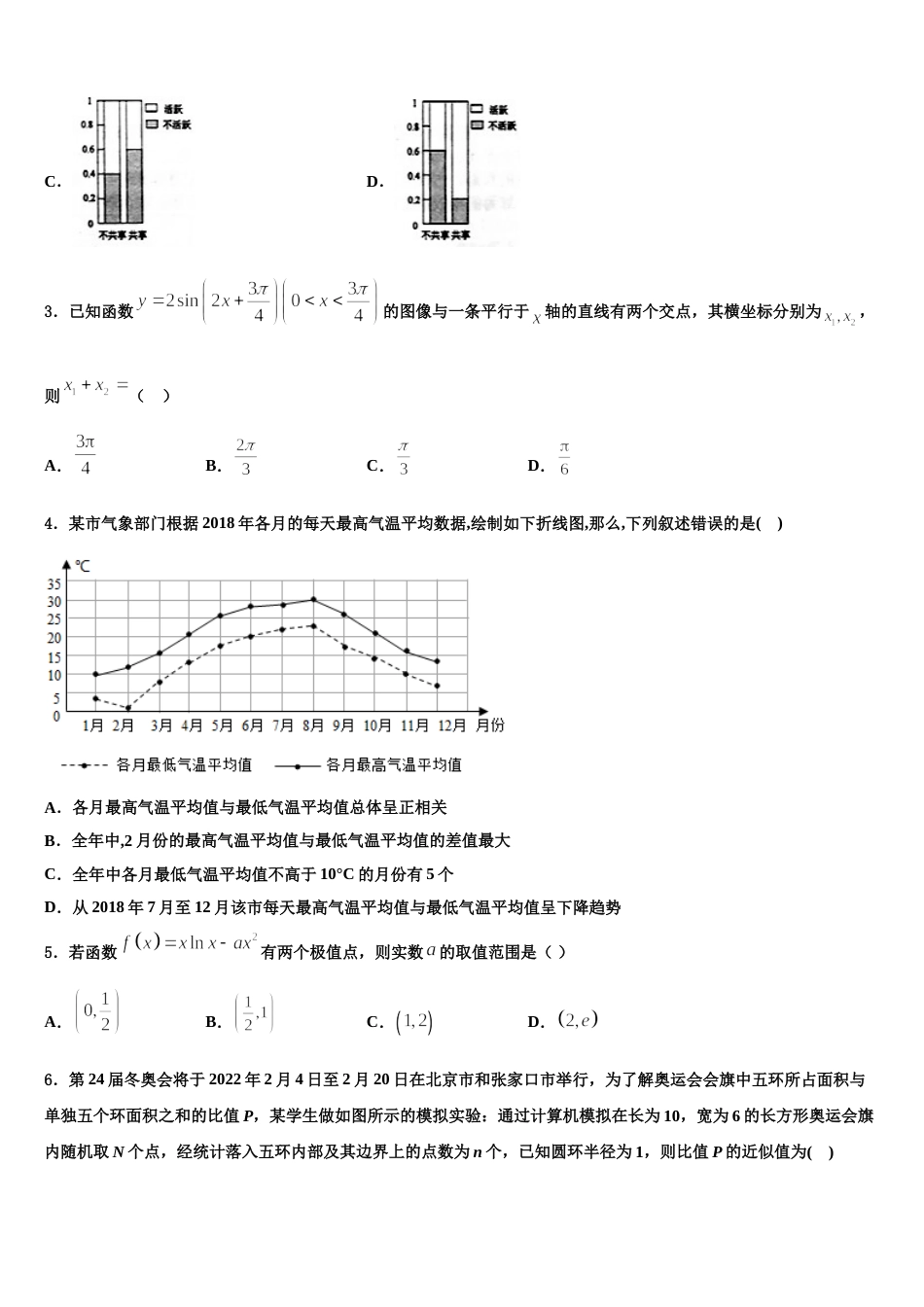
2024 届广东省东莞市重点中学高考冲刺押题(最后一卷)数学试卷注意事项1.考试结束后,请将本试卷和答题卡一并交回.2.答题前,请务必将自己的姓名、准考证号用 0.5 毫米黑色墨水的签字笔填写在试卷及答题卡的规定位置.3.请认真核对监考员在答题卡上所粘贴的条形码上的姓名、准考证号与本人是否相符.4.作答选择题,必须用 2B 铅笔将答题卡上对应选项的方框涂满、涂黑;如需改动,请用橡皮擦干净后,再选涂其他答案.作答非选择题,必须用 05 毫米黑色墨水的签字笔在答题卡上的指定位置作答,在其他位置作答一律无效.5.如需作图,须用 2B 铅笔绘、写清楚,线条、符号等须加黑、加粗.一、选择题:本题共 12 小题,每小题 5 分,共 60 分。在每小题给出的四个选项中,只有一项是符合题目要求的。1.如图,中,点 D 在 BC 上,,将沿 AD 旋转得到三棱锥,分别记,与平面 ADC 所成角为,,则,的大小关系是( )A.B.C.,两种情况都存在 D.存在某一位置使得2.党的十九大报告明确提出:在共享经济等领域培育增长点、形成新动能.共享经济是公众将闲置资源通过社会化平台与他人共享,进而获得收入的经济现象.为考察共享经济对企业经济活跃度的影响,在四个不同的企业各取两个部门进行共享经济对比试验,根据四个企业得到的试验数据画出如下四个等高条形图,最能体现共享经济对该部门的发展有显著效果的图形是( )A.B.C.D.3.已知函数的图像与一条平行于轴的直线有两个交点,其横坐标分别为,则( )A.B.C.D.4.某市气象部门根据 2018 年各月的每天最高气温平均数据,绘制如下折线图,那么,下列叙述错误的是( )A.各月最高气温平均值与最低气温平均值总体呈正相关B.全年中,2 月份的最高气温平均值与最低气温平均值的差值最大C.全年中各月最低气温平均值不高于 10°C 的月份有 5 个D.从 2018 年 7 月至 12 月该市每天最高气温平均值与最低气温平均值呈下降趋势5.若函数有两个极值点,则实数的取值范围是( )A.B.C.D.6.第 24 届冬奥会将于 2022 年 2 月 4 日至 2 月 20 日在北京市和张家口市举行,为了解奥运会会旗中五环所占面积与单独五个环面积之和的比值 P,某学生做如图所示的模拟实验:通过计算机模拟在长为 10,宽为 6 的长方形奥运会旗内随机取 N 个点,经统计落入五环内部及其边界上的点数为 n 个,已知圆环半径为 1,则比值 P 的近似值为( )A.B.C.D.7.一艘海轮从 A 处出发,以每小时 24 海里的速度沿南偏东 40°的方向直线航行,30 分钟后到达 B 处,在 C 处有一座灯塔,海轮在 A 处观察灯塔,其方向是南偏东 70°,在 B 处观察灯塔,其方向是北偏东 65°,那么 B,C 两点间的距离是( )A.6 海里B.6海里C.8海里D.8海里8.已知向量,且,则等于( )A.4B.3C.2D.19.已知的展开式中第项与第项的二项式系数相等,则奇数项的二项式系数和为( ).A.B.C.D.10.在复平面内,复数 z=i 对应的点为 Z,将向量绕原点 O 按逆时针方向旋转,所得向量对应的复数是( )A.B.C.D.11.如图所示的程序框图输出的是 126,则①应为( )A.B.C.D.12.对于定义在上的函数,若下列说法中有且仅有一个是错误的,则错误的一个是( )A.在上是减函数B.在上是增函数C.不是函数的最小值D.对于,都有二、填空题:本题共 4 小题,每小题 5 分,共 20 分。13.某中学高一年级有学生 1200 人,高二年级有学生 900 人,高三年级有学生 1500 人,现按年级用分层抽样的方法从这三个年级的学生中抽取一个容量为 720 的样本进行某项研究,则应从高三年级学生中抽取_____人.14.已知双曲线的一条渐近线为,且经过抛物线的焦点,则双曲线的标准方程为______.15.在的展开式中,所有的奇数次幂项的系数和为-64,则实数的值为__________.16.记数列的前项和为,已知,且.若,则实数的取值范围为________.三、解答题:共 70 分。解答应写出文字说明、证明过程或演算步骤。17.(12 分)已知函数.(1)求函数 f(x)的最小正周期;(2)求...