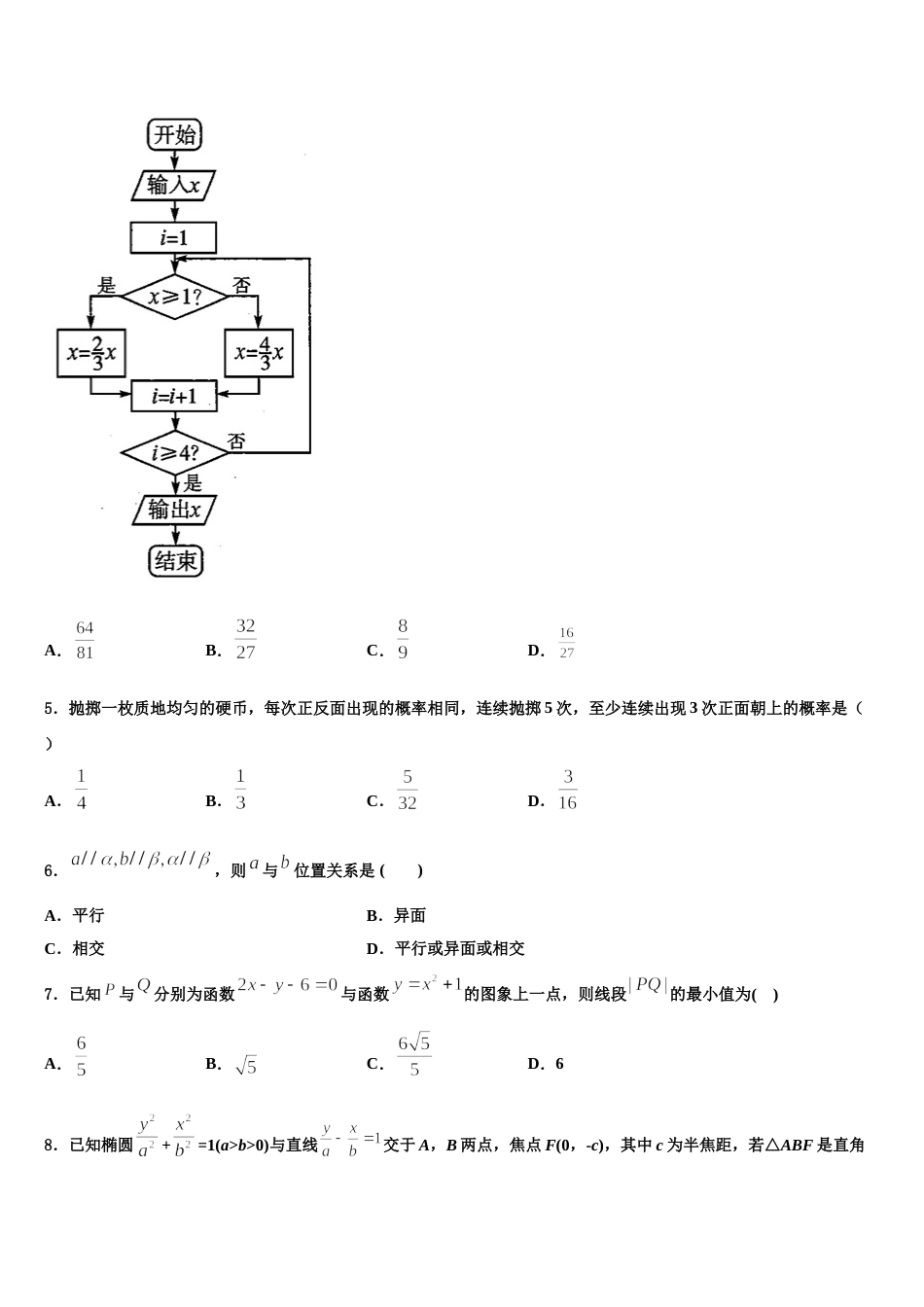
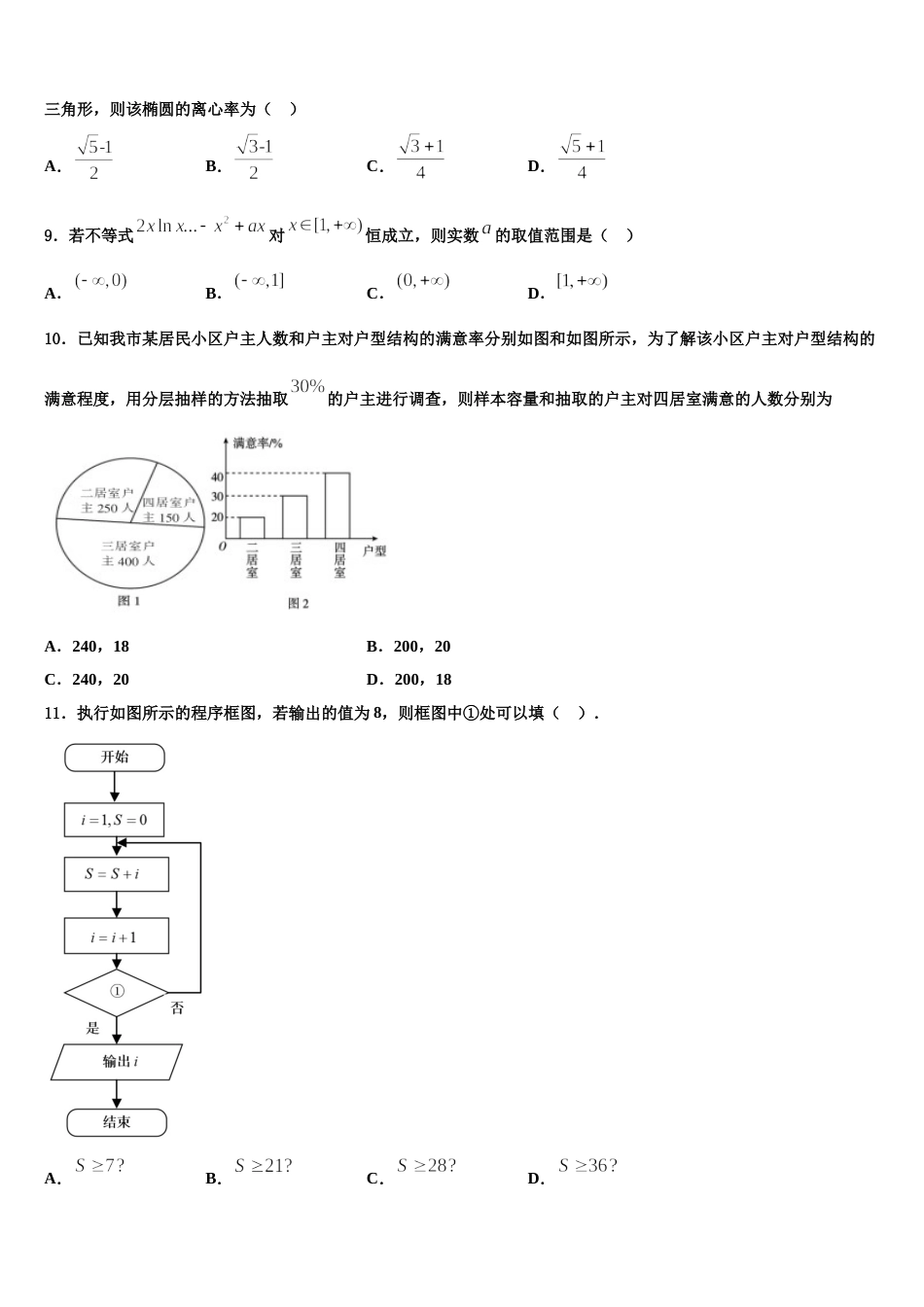
2024 届广东省海珠区等四区高考全国统考预测密卷数学试卷注意事项1.考试结束后,请将本试卷和答题卡一并交回.2.答题前,请务必将自己的姓名、准考证号用 0.5 毫米黑色墨水的签字笔填写在试卷及答题卡的规定位置.3.请认真核对监考员在答题卡上所粘贴的条形码上的姓名、准考证号与本人是否相符.4.作答选择题,必须用 2B 铅笔将答题卡上对应选项的方框涂满、涂黑;如需改动,请用橡皮擦干净后,再选涂其他答案.作答非选择题,必须用 05 毫米黑色墨水的签字笔在答题卡上的指定位置作答,在其他位置作答一律无效.5.如需作图,须用 2B 铅笔绘、写清楚,线条、符号等须加黑、加粗.一、选择题:本题共 12 小题,每小题 5 分,共 60 分。在每小题给出的四个选项中,只有一项是符合题目要求的。1.已知点在双曲线上,则该双曲线的离心率为( )A.B.C.D.2.已知函数满足,设,则“”是“”的( )A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件3.已知向量,,则与的夹角为( )A.B.C.D.4.相传黄帝时代,在制定乐律时,用“三分损益”的方法得到不同的竹管,吹出不同的音调.如图的程序是与“三分损益”结合的计算过程,若输入的的值为 1,输出的的值为( )A.B.C.D.5.抛掷一枚质地均匀的硬币,每次正反面出现的概率相同,连续抛掷 5 次,至少连续出现 3 次正面朝上的概率是( )A.B.C.D.6.,则与位置关系是 ( )A.平行B.异面C.相交D.平行或异面或相交7.已知与分别为函数与函数的图象上一点,则线段的最小值为( )A.B.C.D.68.已知椭圆+=1(a>b>0)与直线交于 A,B 两点,焦点 F(0,-c),其中 c 为半焦距,若△ABF 是直角三角形,则该椭圆的离心率为( )A.B.C.D.9.若不等式对恒成立,则实数的取值范围是( )A.B.C.D.10.已知我市某居民小区户主人数和户主对户型结构的满意率分别如图和如图所示,为了解该小区户主对户型结构的满意程度,用分层抽样的方法抽取的户主进行调查,则样本容量和抽取的户主对四居室满意的人数分别为A.240,18B.200,20C.240,20D.200,1811.执行如图所示的程序框图,若输出的值为 8,则框图中①处可以填( ).A.B.C.D.12.函数的图象如图所示,为了得到的图象,可将的图象( )A.向右平移个单位B.向右平移个单位C.向左平移个单位D.向左平移个单位二、填空题:本题共 4 小题,每小题 5 分,共 20 分。13.已知函数是定义在上的奇函数,且周期为,当时,,则的值为___________________.14.3 张奖券分别标有特等奖、一等奖和二等奖.甲、乙两人同时各抽取 1 张奖券,两人都未抽得特等奖的概率是__________.15.函数过定点________.16.如图,在正四棱柱中,P 是侧棱上一点,且.设三棱锥的体积为,正四棱柱的体积为 V,则的值为________.三、解答题:共 70 分。解答应写出文字说明、证明过程或演算步骤。17.(12 分)选修 4—5;不等式选讲.已知函数.(1)若的解集非空,求实数的取值范围;(2)若正数满足,为(1)中 m 可取到的最大值,求证:.18.(12 分)已知矩形中,,E,F 分别为,的中点.沿将矩形折起,使,如图所示.设 P、Q 分别为线段,的中点,连接.(1)求证:平面;(2)求二面角的余弦值.19.(12 分)已知函数(),不等式的解集为.(1)求的值;(2)若,,,且,求的最大值.20.(12 分)如图 1,在等腰梯形中,两腰,底边,,,是的三等分点,是的中点.分别沿,将四边形和折起,使,重合于点,得到如图 2 所示的几何体.在图 2 中,,分别为,的中点.(1)证明:平面.(2)求直线与平面所成角的正弦值.21.(12 分)在直角坐标系 xOy 中,直线 的参数方程为(t 为参数).以原点 O 为极点,x 轴正半轴为极轴建立极坐标系,圆 C 的极坐标方程为.(1)写出圆 C 的直角坐标方程;(2)设直线 l 与圆 C 交于 A,B 两点,,求的值.22.(10 分)在一次电视节目的答题游戏中,题型为选择题,只有“A”和“B”两种结果,其中某选手选择正确的概率为 p,选择错误的概率为 q,...