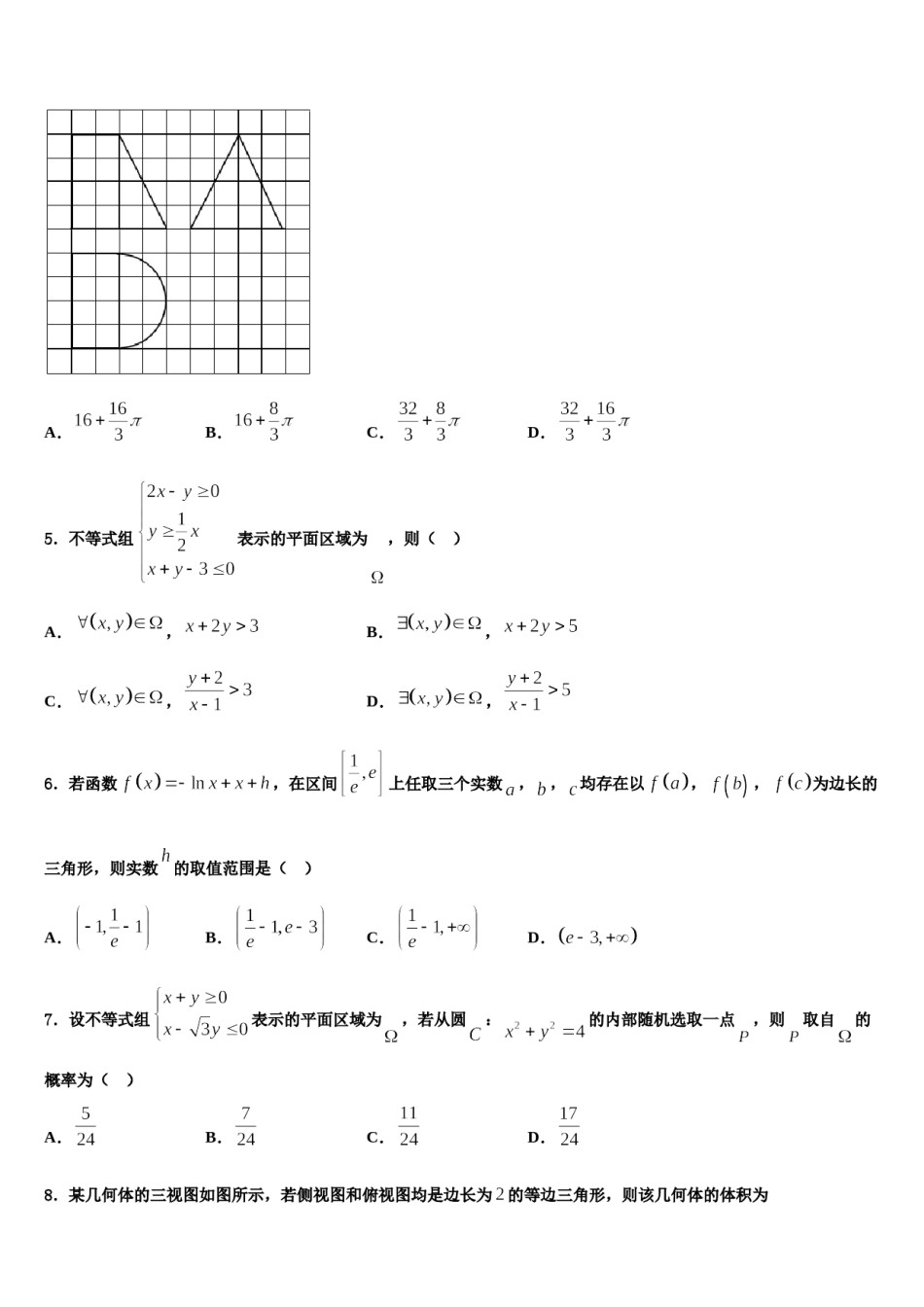
2024届广东省深圳市翠园中学高考数学四模试卷考生须知:1.全卷分选择题和非选择题两部分,全部在答题纸上作答。选择题必须用2B铅笔填涂;非选择题的答案必须用黑色字迹的钢笔或答字笔写在“答题纸”相应位置上。2.请用黑色字迹的钢笔或答字笔在“答题纸”上先填写姓名和准考证号。3.保持卡面清洁,不要折叠,不要弄破、弄皱,在草稿纸、试题卷上答题无效。一、选择题:本题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的。1.在平面直角坐标系中,已知是圆上两个动点,且满足,设到直线的距离之和的最大值为,若数列的前项和恒成立,则实数的取值范围是()A.B.C.D.2.集合,则()A.B.C.D.,3.对两个变量进行回归分析,给出如下一组样本数据:,,,下列函数模型中拟合较好的是()A.B.C.D.4.某几何体的三视图如图所示,若图中小正方形的边长均为1,则该几何体的体积是A.B.C.D.5.不等式组表示的平面区域为,则()A.,B.,C.,D.,6.若函数,在区间上任取三个实数,,均存在以,,为边长的三角形,则实数的取值范围是()A.B.C.D.7.设不等式组表示的平面区域为,若从圆:的内部随机选取一点,则取自的概率为()A.B.C.D.8.某几何体的三视图如图所示,若侧视图和俯视图均是边长为的等边三角形,则该几何体的体积为A.B.C.D.9.已知实数满足约束条件,则的最小值是A.B.C.1D.410.二项式的展开式中只有第六项的二项式系数最大,则展开式中的常数项是()A.180B.90C.45D.36011.若,则“”是“的展开式中项的系数为90”的()A.必要不充分条件B.充分不必要条件C.充要条件D.既不充分也不必要条件12.已知函数,若关于的方程恰好有3个不相等的实数根,则实数的取值范围为()A.B.C.D.二、填空题:本题共4小题,每小题5分,共20分。13.“今有女善织,日益功疾,初日织五尺,今一月共织九匹三丈.”其白话意译为:“现有一善织布的女子,从第2天开始,每天比前一天多织相同数量的布,第一天织了5尺布,现在一个月(按30天计算)共织布390尺.”则每天增加的数量为____尺,设该女子一个月中第n天所织布的尺数为,则______.14.在直角坐标系中,已知点和点,若点在的平分线上,且,则向量的坐标为___________.与函数的图象在y轴右侧的公共点从15.在平面直角坐标系xOy中,己知直线左到右依次为,,…,若点的横坐标为1,则点的横坐标为________.16.在直角三角形中,为直角,,点在线段上,且,若,则的正切值为_____.三、解答题:共70分。解答应写出文字说明、证明过程或演算步骤。17.(12分)已知函数是减函数.(1)试确定a的值;(2)已知数列,求证:.18.(12分)已知函数.(1)若对任意x0,f(x)0恒成立,求实数a的取值范围;(2)若函数f(x)有两个不同的零点x1,x2(x1x2),证明:.19.(12分)设点分别是椭圆的左,右焦点,为椭圆上任意一点,且的最小值为1.(1)求椭圆的方程;(2)如图,直线与轴交于点,过点且斜率的直线与椭圆交于两点,为线段的中点,直线交直线于点,证明:直线.20.(12分)已知函数,.(1)若对于任意实数,恒成立,求实数的范围;(2)当时,是否存在实数,使曲线:在点处的切线与轴垂直?若存在,求出的值;若不存在,说明理由.中,底面为直角梯形,,,,21.(12分)如图,在四棱锥,,点、分别为,的中点,且平面平面.(1)求证:平面.(2)若,求直线与平面所成角的正弦值.22.(10分)某企业为了了解该企业工人组装某产品所用时间,对每个工人组装一个该产品的用时作了记录,得到大量统计数据.从这些统计数据中随机抽取了个数据作为样本,得到如图所示的茎叶图(单位:分钟).若用时不超过(分钟),则称这个工人为优秀员工.(1)求这个样本数据的中位数和众数;(2)以这个样本数据中优秀员工的频率作为概率,任意调查名工人,求被调查的名工人中优秀员工的数量分布列和数学期望.参考答案一、选择题:本题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的。1、B【解析】由于到直线的距离和等于中点到此...